4621
Spatially Fourier Excited Acquisition and Reconstruction (SFEAR) for Improved Slice Acceleration
Negin Yaghmaie1,2, Warda Syeda3, Yasmin Blunck1,2, Bahman Tahayori4, Rebecca K. Glarin2,5, Bradford A. Moffat2,6, and Leigh A. Johnston1,2
1Department of Biomedical Engineering, The University of Melbourne, Melbourne, Australia, 2Melbourne Brain Centre Imaging Unit, The University of Melbourne, Melbourne, Australia, 3Melbourne Neuropsychiatry Centre, The University of Melbourne, Melbourne, Australia, 4The Florey Institute of Neuroscience and Mental Health, Melbourne, Australia, 5Department of Radiology, Royal Melbourne Hospital, Melbourne, Australia, 6Department of Medicine and Radiology, The University of Melbourne, Melbourne, Australia
1Department of Biomedical Engineering, The University of Melbourne, Melbourne, Australia, 2Melbourne Brain Centre Imaging Unit, The University of Melbourne, Melbourne, Australia, 3Melbourne Neuropsychiatry Centre, The University of Melbourne, Melbourne, Australia, 4The Florey Institute of Neuroscience and Mental Health, Melbourne, Australia, 5Department of Radiology, Royal Melbourne Hospital, Melbourne, Australia, 6Department of Medicine and Radiology, The University of Melbourne, Melbourne, Australia
Synopsis
Keywords: New Trajectories & Spatial Encoding Methods, New Trajectories & Spatial Encoding Methods
A new 3D Spatially Fourier Excited Acquisition and Reconstruction method (SFEAR) is introduced, in which double-RF pulses are used to excite sinusoidally-modulated slice profiles across a slab. Target spatial frequencies are achieved by varying the time shift between the two pulses, to construct the slice-phase-encode dimension of 3D k-space from Fourier excited acquisitions. SFEAR outperforms conventional GRAPPA in the slice-phase encode dimension, given its inherent ability to undersample sine or cosine components rather than whole planes of 3D k-space. Superior reconstruction of undersampled data and lower g-factor values are demonstrated in both 7T phantom and in vivo data.Introduction
Spatially selective RF excitation pulses have been used to encode MR images using non-Fourier basis sets such as wavelet encoding and SVD decomposition1,2,3 to spread MR signal’s energy in k-space in the context of Compressed Sensing4, 5. In this work, we exploit the linear response model6 of selective excitation and introduce a Spatially Fourier Excited Acquisition and Reconstruction (SFEAR) technique that encodes magnetization using sinusoidally-modulated excitation and constructs a 3D k-space from the cosine- and sine-modulated, slab selective excitations. The 3D image volume is returned simply by inverse Fourier transform. Following proof-of-principle demonstration of SFEAR, the strength of SFEAR is demonstrated in slice-phase encode undersampling using a modified GRAPPA7 reconstruction algorithm. Rather than dropping whole planes in 3D k-space, SFEAR can selectively drop cosine- and sine-components, thus acquiring partial information at a greater number of 3D k-space planes. The robustness of SFEAR in slice-undersampled data is demonstrated on both 7T phantom and in-vivo datasets, without the need for Compressed Sensing sparsity regularization terms or other forms of penalty functions.Theory
SFEAR Excitation: In 3D image acquisition, 3D k-space is encoded by readout, phase encode and slice-phase encode dimensions, kx, ky and kz (assigned without loss of generality), respectively. Our proposal of Spatially Fourier Excited Acquisition uses Euler’s identity, $$$e^{-jk_z z}=cos(k_{z}z)-jsin(k_{z}z)$$$, to decompose the slice-phase encode dimension into its cosine and sine components, moving each to the RF excitation; double-RF pulses encode either a cosine or sine-modulation of the magnetization (Fig.1). The desired set of (N+1) kz frequencies are obtained by a set of time shifts, Δ, between the double-RF pulses, calculated from $$$k_{z_i}=\gamma G_{ss}\Delta_i$$$, $$$i=0,\dots, \lfloor N/2\rfloor$$$, for a given slice select gradient magnitude, Gss, with corresponding to a base pulse with twice the magnitude of the non-zero kz frequencies. Sine-modulated profiles are achieved by applying phases of 90° and -90° to the first and second pulses, respectively, of the cosine-modulated case. Each SFEAR acquisition is a slab-selective excitation, with profile determined by the base pulse, followed by a 2D readout. SFEAR Reconstruction: The ith positive and negative planes of the SFEAR 3D k-space, SSFEAR, are constructed from Sc and Ss, the 2D k-space planes acquired under cosine- and sine-modulation, respectively, for variable time shift, $$$\Delta_i=k_{z_i}/{\gamma G_{ss}}$$$:$$S^{SFEAR} (k_x, k_y, k_{z_i})=S_c(k_x, k_y, \Delta_i)-jS_{s}(k_x, k_y, \Delta_i), $$
and
$$S^{SFEAR}(k_x, k_y, -k_{z_i})=S_c(k_x, k_y, \Delta_i)+jS_{s}(k_x, k_y, \Delta_i).$$
Thus, SFEAR 3D k-space with (N+1)kz planes is constructed by (N/2+1) cosine and N/2 sine encodings, analogous to a Fourier series representation of the data. Slice-phase encode acceleration: A modified GRAPPA algorithm estimates the fully-sampled k-space from undersampled SFEAR data (Fig. 2), using an undersampling pattern that can alternate sine- and cosine-modulated acquisitions. For an undersampling factor of Rz=2, no 3D k-space planes are left without partial acquisition of information, in contrast to the conventional approach of dropping entire planes of 3D k-space.
Methods
Experiments: An in-house 3D printed resolution phantom and a 27-year-old volunteer were scanned using SFEAR via a modified Flash sequence (slab thickness = 7 mm, 21 slices of thickness = 0.33 mm, Gss=21.8 mT/m , Δi$$$\in$$${0, 156, 313, 469, 626, 782, 939, 1096, 1255,1409, 1558} μs , TE = 20 ms, TR = 300 ms, FA = 15°, in-plane resolution = 0.78 × 0.78 mm, scan time = 28 minutes). 3D FLASH acquisitions with the same parameters and same scan time were acquired for comparison. Slice acceleration: Data was retrospectively undersampled and reconstructed using a kernel size of 5×5×5 and an autocalibration space consisting of the 10 central k-space planes. To obtain g-factor measurements from the phantom, 100 noisy reconstructions were pseudo-replicated8 in simulation using the coil noise covariance matrix measured with a noise-only scan at the beginning of the experiment.Results
Phantom: The reconstructed fully-sampled phantom images (Fig. 3) provide a proof-of-principle that SFEAR replicates the image quality and structural detail of 3D FLASH. In undersampling in the slice-phase encode dimension, SFEAR clearly outperforms GRAPPA. GRAPPA reconstructions contain noisy regions that are absent in the undersampled SFEAR images. The g-factor maps show consistently lower values in the undersampled 3DBEE reconstruction. In-vivo: As with the phantom results, fully sampled in-vivo SFEAR replicates 3D FLASH (Fig. 5). Undersampled SFEAR (Rz=2) maintains image quality, in contrast to the noisy regions present in the conventional GRAPPA reconstructions.Discussion and Conclusion
Proof-of-principle of the Spatially Fourier Excited Acquisition and Reconstruction method, that moves the slice-phase encode dimension into the excitation, has been demonstrated in phantom and in-vivo experiments. SFEAR pulses have half the SAR of the slab selective pulses applied in conventional 3D acquisitions. Considering the small size of the autocalibration set, the noisy results achieved by GRAPPA are consistent with previous studies9, while SFEAR reconstructions returned smaller g-factors and markedly better unaliasing of the slices, despite there being only 21 slices in the exemplar volumes. Our current pilot results are promising for SFEAR outperforming GRAPPA at higher undersampling factors also. SFEAR undersampling can also be combined with in-plane GRAPPA to further accelerate acquisitions. The implicit property of SFEAR that permits robust undersampling of the slice-phase encode dimension without requiring regularization offers great promise for future combination of SFEAR and Compressed Sensing for further acceleration of 3D imaging.Acknowledgements
We acknowledge the facilities, the scientific and technical assistance of the Australian National Imaging Facility, a National Collaborative ResearchInfrastructure Strategy (NCRIS) capability, at the Melbourne Brain Centre Imaging Unit of the University of Melbourne. The work is supported by a research collaboration agreement with Siemens Healthineers.References
[1] Bolinger and Leigh. JMR. 1988. [2] Gelman and Wood. MRM. 1996. [3] Panych et al. MRM. 1996. [4] Wang et al. ISMRM. 2012. [5] Wang et al. ISMRM. 2009 [6] Panych et al. Int J Imaging Syst Technol. 1999. [7] Griswold et al. MRM. 2002. [8] Robson et al. MRM. 2008. [9] Blaimer et al. MRM. 2006.Figures
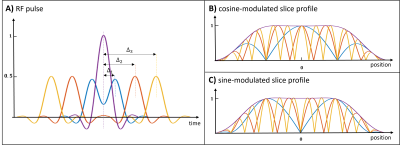
Fig 1. A) Exemplar normalized
cosine-modulated excitation RF pulses overlaid with the base sinc pulse (purple
line). The double-RF pulses are generated by addition of two base sinc pulses
with a set of time shifts, Δi, generating a set of
spatial frequencies. B) Corresponding normalized cosine-modulated slice
profiles overlaid with slice profile of the base sinc pulse (purple line). C)
Sine-modulated slice profiles (RF pulses not shown), achieved by applying
phases of 90° and -90° to the first and second pulse, respectively, of the
cosine-modulated case).
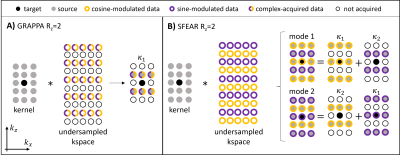
Fig 2. A comparison of parallel imaging kernels
for slice acceleration: Diagrams represent 2D
projections of 3D kernels and 3D k-space (each row of circles represents a
plane in 3D k-space of all coils). A) GRAPPA (Rz = 2). B)
SFEAR (Rz = 2) decomposed into mode 1 (kernel’s centre acquired
using cosine-modulated excitation) and mode 2 (kernel’s centre acquired using
sine-modulated excitation). Sub-kernels κ1 and κ2 depict different
source-target positions.
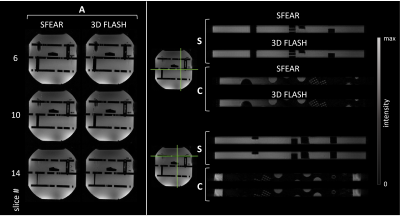
Fig 3. Fully-sampled phantom image comparison: Axial slices (A) of SFEAR (left) and 3D
FLASH (right), validating the SFEAR proof-of-concept that the slice-phase
encode dimension can be decomposed into cosine and sine components and moved to
the excitation. Sagittal (S) and Coronal (C) slices of SFEAR (top of each image
pair) and 3D FLASH (bottom of each image pair) demonstrate near-identical
delineation of the resolution grid in both acquisitions.
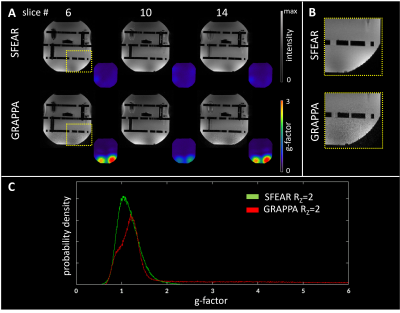
Fig 4. Improved slice acceleration using SFEAR: A) Selected axial slices of SFEAR Rz =2 and GRAPPA Rz
=2 where better unaliasing of the slices is observed. Colored inlaid images are
g-factor maps. B) Zoomed-in sections depict noisy regions in GRAPPA that
are not present in SFEAR. C) Histograms of g-factors show a heavier-tailed
distribution for GRAPPA.
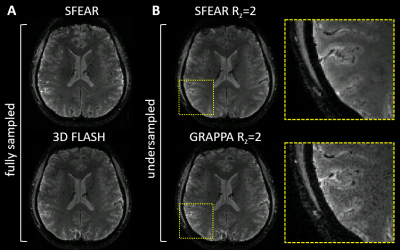
Fig 5. Selected axial slice of in-vivo data. A) Fully-sampled
dataset comparing SFEAR and 3D FLASH. B) Slice-phase encode undersampled
(Rz=2) results are consistent with the phantom study, with noisy
regions in conventional GRAPPA (highlighted in the zoomed-in sections) that are
ameliorated in SFEAR.
DOI: https://doi.org/10.58530/2023/4621