Synopsis

Keywords: Image Reconstruction, Data Acquisition, De-noising

Significant efforts are focused on maximizing SNR in high spatial and temporal resolution image acquisitions. We present a method of utilizing GRAPPA to de-noise k-space observations made with a multi-channel array. By replacing a fully sampled observed k-space with a k-space in which each observation is inferred from a weighted average of neighboring observations across all coils, an increase of SNR on the order of 5% is achieved.

Introduction

As imaging applications continue to push the boundaries of spatial and temporal resolution, compromises are introduced in image quality. Signal-to-noise ratio (SNR) and temporal signal-to-noise ratio (tSNR) degrade with voxel volume, acquisition acceleration, and reduced excitation tip angles with shorter repetition times when the Ernst angle is used. Tremendous effort has been directed towards addressing such degradation through numerous de-noising techniques {1}. Several years ago, the mathematics of SENSE were shown to yield 'optimal' coil combination results when a reduction factor of 1 is used {2}. In this work, an analogous application in k-space of GRAPPA with a unity reduction factor is considered when a multi-channel receive coil is employed. Given the effective convolution of k-space observations with the Fourier transform of the image-space coil profile {3}, a correlation of neighboring observations of k-space is present and it is hypothesized that each k-space observation can be replaced through a weighted average of its neighboring observations, and that this fitting can reduce noise of individual observations in the k-space domain.

Methods

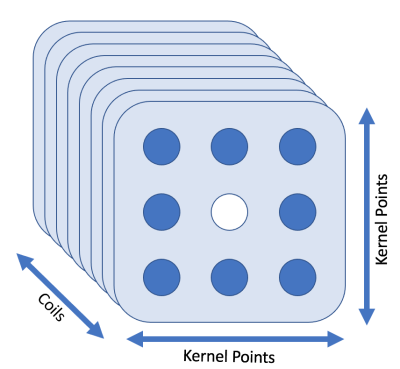
Phantom and human imaging were performed on a GE Healthcare Signa Premier 3.0T MRI system (GE Healthcare, Waukesha WI) with a 48-channel head receive coil. To differentiate impacts of traditional acceleration techniques from the proposed GRAPPA R=1 de-noising, a time series of fully sampled gradient recalled echo (GRE) echo planar imaging (EPI) images were acquired (human: matrix 96x96, TE 30ms, TR 2000ms, flip 70degrees, 150 repetitions, FOV 22cm, slice thickness 2mm; fBIRN phantom: matrix 64x64, TE 30ms, TR2500ms, flip 90degrees, 150 repetitions, FOV 22cm, slice thickness 4mm).

GRAPPA R=1 reconstruction was performed with a standard GRAPPA algorithm in which a convolutional kernel of 3x3 voxels in-plane and 48 channels was fit over all k-space observations with non-zero weights for all voxels except the center voxel, as shown in Fig. 1. The fit kernel was then applied to infer a full k-space. Because GRAPPA kernels are known to poorly account for the high signal-to-noise ratio and rapid intensity fluctuations at the center of k-space {4}, the central 10x10 voxels of k-space were preserved from the initial acquisition.

The proposed GRAPPA k-space de-noising algorithm was also applied following two-fold simulated in-plane acceleration. In short, odd k-space lines were removed from the dataset, even lines were interpolated following the above described GRAPPA R=1 algorithm, and odd lines interpolated following a traditional GRAPPA reconstruction with a kernel size of 3 voxels. The central 10x10 voxels of k-space included the original even lines and the interpolated odd lines based upon the original even lines.

In all cases, resulting coil images were combined through a simple sum of squares, and point-wise intensity weighted average. To assess performance, temporal signal to noise ratio (tSNR) was calculated over the time series.

Results

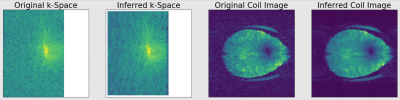
The GRAPPA R=1 de-noising algorithm yields improvements in tSNR in all data sets without simulated acceleration, and performs equivalently when in-plane acceleration is simulated. In the phantom, tSNR improved from 194 to 206 (6.2%, Wilcoxon p<1e-13) in the intensity weighted combination and from 193 to 204 (5.3%, Wilcoxon p<1e-9) in the root sum of squares combination without in-plane acceleration. In the human, tSNR improved from 68.8 to 71.7 (4.2%, Wilcoxon p<1e-15) in the intensity weighted combination and from 69.0 to 71.7 (3.9%, Wilcoxon p<1e-15) in the root sum of squares combination without in-plane acceleration. In the presence of in-plane acceleration, impact of performing GRAPPA R=1 de-noising prior to fitting GRAPPA kernes for accelerated imaging yielded unchanged tSNR in all tested cases.

Discussion

As spatial and temporal resolution of MR acquisitions continue to progress, techniques to maximize the signal-to-noise ratio in reconstructed images are of growing importance. In this work we presented a technique to de-noise k-space observations through the mathematics of GRAPPA with a unity acceleration factor. Most significant impact from this GRAPPA R=1 de-noising is shown in cases where GRAPPA interpolation is not already in use to infer k-space observations which were not acquired due to acceleration. When GRAPPA interpolation is applied in a reconstruction pipeline to infer omitted observations, the impact of the GRAPPA R=1 de-noising is unsurprisingly reduced because the k-space convolution is already imposed through the unaliasing process.

Conculsion

Because of g-factor penalties faced with parallel imaging, parallel imaging is generally eliminated prior to increasing the number of averages in an acquisition. This work suggests that an increase of signal-to-noise ratio on the order of 5% can be achieved in these un-accelerated, single-average acquisitions by applying a GRAPPA R=1 k-space data fitting and interpolation prior to performing standard reconstruction. As such, a simple modification of adding GRAPPA reconstruction with a simple kernel shown in Figure 1 can be made to existing reconstruction and image processing algorithms to achieve enhanced image quality.

Acknowledgements

The authors would like to thank the institution's research coordinator and MRI technologist teams.