4616
Non-Linear Reconstruction for Coil Sensitivity Calibration from Cartesian and non-Cartesian Data
H. Christian M. Holme1 and Martin Uecker1,2,3,4
1Institute of Biomedical Imaging, Graz University of Technology, Graz, Austria, 2Institute for Diagnostic and Interventional Radiology, University Medical Center Göttingen, Göttingen, Germany, 3Partner Site Göttingen, DZHK (German Centre for Cardiovascular Research), Göttingen, Germany, 4Cluster of Excellence “Multiscale Bioimaging: from Molecular Machines to Networks of Excitable Cells” (MBExC), University of Göttingen, Göttingen, Germany
1Institute of Biomedical Imaging, Graz University of Technology, Graz, Austria, 2Institute for Diagnostic and Interventional Radiology, University Medical Center Göttingen, Göttingen, Germany, 3Partner Site Göttingen, DZHK (German Centre for Cardiovascular Research), Göttingen, Germany, 4Cluster of Excellence “Multiscale Bioimaging: from Molecular Machines to Networks of Excitable Cells” (MBExC), University of Göttingen, Göttingen, Germany
Synopsis
Keywords: Parallel Imaging, Parallel Imaging
We compare the current de-facto standard for coil sensitivity calculation, ESPIRiT, to a non-linear reconstruction method, ENLIVE. While ENLIVE normally produces both images and coil sensitivies, we focus here on using it for calibration of the coil sensitivities. We applied ESPIRiT and ENLIVE to low-resolution subsets of a 3D Cartesian and a non-Cartesian spiral acquisition, using the resoluting coil profiles in a linear parallel imaging reconstruction. We showed that ENLIVE is substantially faster for a high number of channels and provides improved sensitivities in the non-Cartesian example.Introduction
Current accelerated MRI reconstruction is generally a two-step process: coil sensitivities are calculated in a calibration step, which are then used for image reconstruction. This pre-calculation converts the non-linear parallel MRI problem into a linear inverse problem.While several methods for coil sensitivity calculation exist, ESPIRiT [1] has in recent years emerged as a de-facto standard in MRI research. It is based on the singular value decomposition (SVD) of an image space operator. Since the SVD has an unfavorable scaling with the matrix size, ESPIRiT scales poorly with the number of receive channels.
Another disadvantage of current coil calibration methods is that they need a relatively large calibration region in the k-space center.
Iterative SVD-based methods such as SAKE [2] can be applied to partially undersampled calibration data, but are even more computationally demanding, as they use the SVD inside of an iterative algorithm.
For this reason, the use of non-linear methods such as Regularized Non-Linear Inversion (NLINV) [3] or Extended NonLinear InVersion inspired by ESPIRiT (ENLIVE) [4] as a calibration step for linear reconstruction methods is an attractive alternative.
While both methods are normally used as full reconstruction methods which yield both images and coil sensitivities, we focus here on their use for coil sensitivity estimation.
In contrast to ESPIRiT, NLINV cannot make use of multiple maps which is needed to avoid artifacts in certain scenarios.
ENLIVE is an extension of NLINV to multiple maps which should be just as robust as ESPIRiT.
In [5], ENLIVE was used to calculate coil sensitivities to reconstruct self-gated cardiac MRI data.
NLINV (that is, ENLIVE with a single map) has also been used to calculate coil sensitivities for model-based T1-mapping [6,7].
In this work, we compared ESPIRiT [1] and ENLIVE [4] as methods for calculating coil sensitivities.
Methods
We applied ESPIRiT and ENLIVE to two different datasets:First, on a Cartesian 3D MPRAGE acquisition of the brain of a volunteer acquired with a 64-channel head coil at 3 T. Sequence parameters are TR/TE: 2300 ms/2.27 ms, flip angle: 8°, matrix size: 448×224×224, resolution: 1×1×1 mm³. This dataset was undersampled in the two phase-encoding directions using 4x Poisson-disc undersampling.
A central region of size 72×48×48 was extracted, compressed with an SVD to 2 to 64 channels, and then coil sensitivities were calculated using ESPIRiT and ENLIVE with 2 maps.
Second, on a non-Cartesian GE spiral brain dataset with 3 interleaves from Maier et al. [8], acquired using a 16-channel head coil at 3 T. Sequence parameters are TR/TE: 2000 ms/25 ms, flip angle: 90°, FOV: 220x220 mm², pixel size: 1x1 mm², slice thickness: 2 mm and 27121 samples per spiral. Here, a subset of the data was gridded to form a low-resolution 48x48 k-space. Then, ESPIRiT and ENLIVE using 1 and 2 maps were applied to calculate coil sensitivities.
In both cases, the small coil profiles were scaled up to the full image size (448x224x224 and 220x220, respectively) by zero-padding in Fourier space and then used in a linear reconstruction.
All reconstructions were done using the Berkeley Advanced Reconstruction Toolbox (bart) [9].
Results and Discussion
To show that both ESPIRiT and ENLIVE provide accurate coil profiles in the Cartesian case, selected orthogonal slices for 16 channels are shown in Figure 1.Figure 2 shows the runtimes of ESPIRiT and ENLIVE.
Even though ESPIRiT is faster for few channels, it scales between quadratically and cubically with the number of channels, while ENLIVE scales linearly. Therefore, ENLIVE is significantly faster for a higher number of channels.
In the non-Cartesian example (Figure 3), the reconstrucions using 1 map are both artifact free. However, for 2 maps, the scaled-up ESPIRiT maps show a high-intensity artifact (indicated by a red circle in Figure 3), which is not present in the reconstruction using ENLIVE coil sensitivites.
The source of this artifact can be seen in Figure 4: In the scaled-up ESPIRiT maps (left), two phase poles are visible. These lead to artificially low signal in map #1 and artificially high signal in map #2, which lead, when combined, to the artifact in Figure 3. In ESPIRiT maps calculated from full-size (220x220) data (Figure 4 right), no such phase poles exist. However, even these maps point to a potential problem: the second ESPIRiT map should be zero in this example, as it is not needed. This is likely caused by errors in the gridded non-Cartesian data.
ENLIVE, on the other hand, does not produce artifacts when upscaling the sensitivities because its coil profiles are smooth by construction: it includes a regularization penalizing high frequencies in the sensitivities [3,4]. Furthermore, the non-linear reconstruction can better restore the undersampled or non-Cartesian calibration region.
Conclusion and Outlook
We have shown that ENLIVE can be used to calculate accurate and robust coil sensitivity profiles in both 3D-Cartesian and non-Cartesian settings. In the 3D case, it is much faster than ESPIRiT. Additionally, as shown in the non-Cartesian case, its coil sensitivities can be scaled up without introducing artifacts.Acknowledgements
No acknowledgement found.References
[1]: Uecker M et al.: "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA", Magn. Reson. Med. 2014; 71:990-1001. DOI: 10.1002/mrm.24751[2]: Shin PJ et al.: "Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion", Magn. Reson. Med. 2014; 72:959-970. DOI: 10.1002/mrm.24997
[3]: Uecker M et al.: "Image reconstruction by regularized nonlinear inversion — joint estimation of coil sensitivities and image content", Magn. Reson. Med. 2008; 60:674–682. DOI: 10.1002/mrm.21691
[4]: Holme HCM et al.: "ENLIVE: An Efficient Nonlinear Method for Calibrationless and Robust Parallel Imaging", Sci. Rep. 2019; 9:3034. DOI: 10.1038/s41598-019-39888-7
[5]: Rosenzweig S et al.: "Cardiac and Respiratory Self-Gating in Radial MRI Using an Adapted Singular Spectrum Analysis (SSA-FARY)", IEEE Trans. Med. Imaging. 2020; 39:3029-3041. DOI: 10.1109/TMI.2020.2985994
[6]: Roeloffs V et al.: "Model-based reconstruction for T1 mapping using single-shot inversion-recovery radial FLASH", Int. J. Imag. Syst. Tech. 2016; 26:254-263. DOI: 10.1002/ima.22196
[7]: Wang X et al.: "High-resolution myocardial T1 mapping using single-shot inversion recovery fast low-angle shot MRI with radial undersampling and iterative reconstruction", Brit. J. Radiol. 2016; 89:20160255. DOI: 10.1259/bjr.20160255
[8]: Maier O et al.: "CG‐SENSE revisited: Results from the first ISMRM reproducibility challenge", Magn. Reson. Med. 2020; 00:1-19. DOI: 10.1002/mrm.28569
[9]: Uecker M et al.: bart 0.8.00 "Toolbox for Computational Magnetic Resonance Imaging", DOI: 10.5281/zenodo.7110562
Figures
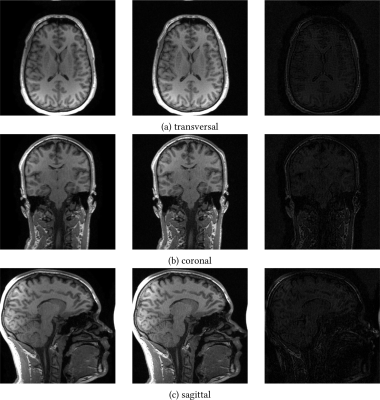
Figure 1: Selected orthogonal slices of a linear parallel imaging reconstruction with coil profiles calculated by ESPIRiT (left) and ENLIVE (center) together with their difference (right) scaled by a factor of ×2. For this reconstruction, the original data was compressed to 16 virtual channels using an SVD.
Both reconstructions show comparable and high quality, showing that both ESPIRiT and ENLIVE provided accurate coil sensitivity profiles.
Both reconstructions show comparable and high quality, showing that both ESPIRiT and ENLIVE provided accurate coil sensitivity profiles.
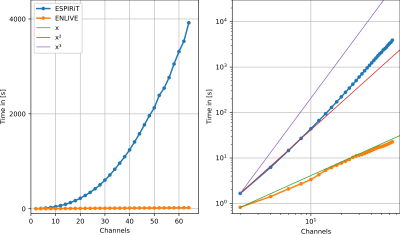
Figure 2: Left: Time needed for the calculation of the coil sensitivities using both ENLIVE and ESPIRiT.
Right: log-log-plot of the same data, with lines showing linear, quadratic and cubic growth. For easier comparison, the
line showing linear growth is scaled to start at the first ENLIVE point, the lines for quadratic and cubic growth start at the first point for ESPIRiT.
We can see that ESPIRiT comparatively fast for small numbers of coils (<8), but that ENLIVE scales approximately linearly with the number of coils whereas ESPIRiT scales between quadratically and cubically.
Right: log-log-plot of the same data, with lines showing linear, quadratic and cubic growth. For easier comparison, the
line showing linear growth is scaled to start at the first ENLIVE point, the lines for quadratic and cubic growth start at the first point for ESPIRiT.
We can see that ESPIRiT comparatively fast for small numbers of coils (<8), but that ENLIVE scales approximately linearly with the number of coils whereas ESPIRiT scales between quadratically and cubically.
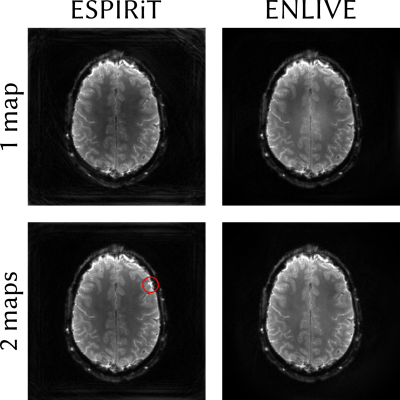
Figure 3: Linear parallel imaging reconstruction of spiral data using ESPIRiT (left) and ENLIVE (right) with 1 (top) or 2 (bottom) maps. ESPIRiT using 1 map and ENLIVE show artifact free reconstruction, while ESPIRiT using 2 maps shows a high-itensity artifact (indicated by the red circle).
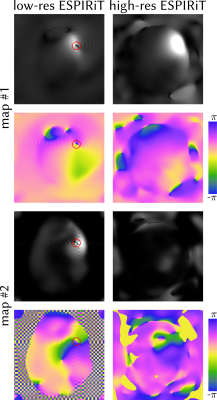
Figure 4: Magnitude and phase of a selected ESPIRiT coil profile calculated from the low-resolution 48x48 k-space (left) and from the full gridded 220x220 k-space (right). The location of the high-itensity artifact in Figure 3 is indicated by a red circle, showing that it is a consequence of two phase poles appearing in both map #1 and map #2. The coil profiles calculated from the full k-space (right) do not show these phase poles.
DOI: https://doi.org/10.58530/2023/4616