4610

Research on Denoising of Magnetic Resonance Spectrum Based on Exponential Decomposition Constraint

Jinyu Wu¹, Tianyu Qiu¹, Zhangren Tu¹, Di Guo², and Xiaobo Qu¹
¹Department of Electronic Science, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China, ²School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China

Synopsis

Keywords: Data Processing, PET/MR

Nuclear Magnetic Resonance (NMR) has been a frequently-used analytical tool in many areas of modern biology, chemistry and medicine for decades. However, it is usually limited by a low Signal-to-Noise ratio (SNR). In practical applications, Signal Averaging (SA) with repeated samplings is required to improve the signal-to-noise ratio, which greatly increases the scanning time. In this paper, based on the characteristic that NMR time-domain signals can be decomposed exponentially, a model for denoising NMR spectroscopy based on exponential decomposition constraints is proposed. It can effectively improve the denoising ability and therefore save the scanning time.

Purpose

For decades, nuclear magnetic resonance (NMR) has been used in many fields of modern biology, chemistry and medicine. However, it usually has a low signal-to-noise ratio (SNR). NMR spectroscopy denoising refers to extract clean signal form original one with noise, usually modeled as Gaussian noise and therefore enhance the SNR of NMR signal, which is a fundamental theme of NMR signal processing. Signal averaging is one of the common methods to enhance the SNR, but it is extremely time-consuming. In the past decades, many methods of signal post-processing have been developed to solve the problem of low SNR of NMR spectra^{1, 2}, such as wavelet denoising³, linear filters⁴, TSVD singular value truncation⁵, Cadzow signal enhancement method^6,7, rQRd⁸ and CHORD⁹. Here, we proposed a novel method for denoising NMR spectroscopy signals based on exponential decomposition constraints¹⁰, which takes full advantage of the low-rank properties and exponential structure of the time domain signal. Compared with classical NMR spectral denoising methods such as rQRd and Cadzow, this method has better denoising performance and is more robust to the setting of exponentials number. Compared with CHORD, this method has better denoising performance in low signal-to-noise ratio signals.

Method

The time domain of NMR spectroscopy which is called Free Induction Decay (FID) is typically modeled as the sum of a set of decaying exponential signals, i.e. the time-domain signal can be exponentially decomposed^{11, 12}. FID can be constructed as a Hankel matrix and the matrix has low-rank properties, which means the matrix rank, the number of exponential components and the number of peaks should be the same¹³. Although Singular values decomposition (SVD) is widely used in classical denoising methods, its physical meaning is not directly clear. Vandermonde factorization of Hankel matrix is another important decomposition method, which generates a series of exponential subspaces, corresponding to the components of FID signals¹⁴. Therefore, we proposed a model for denoising NMR spectroscopy signals based on exponential decomposition constraints, which behaves as the product of a Vandermonde matrix and a 1D vector:
$$\mathop {\min }\limits_\mathbf{x,c,Z} {\left\|\mathcal{R} {{\rm{\mathbf{x}}}} \right\|_*}+{\rm{ }}\frac\lambda2 {\left\| {{\rm{\mathbf{y}-\mathbf{x}}}} \right\|_2^2} + \frac{\gamma}{2}\left\| \mathbf{c} \right\|_2^2 \quad s.t.\mathbf{x}=\mathbf{Zc}, \; \mathbf{Z}\;is\;a\;Vandermonde \; matrix$$(1)
, where $$$\mathcal{R}$$$ denotes the operator which can convert a matrix to a Hankel matrix. $$$\mathbf{x}$$$ and $$$\mathbf{y}$$$ are the observed noisy signal and the signal to be denoised respectively. $$$\mathbf{Z}$$$ is a vandermonde matrix and $$$\mathbf{c}$$$ is a 1D vector. $$$\lambda$$$ and $$$\gamma$$$ denote the regularization parameters. The model can be further solved with the Alternating Direction Method of Multipliers (ADMM)^15,16.

Results

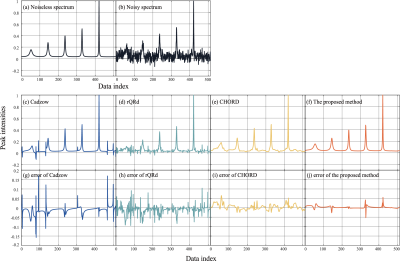
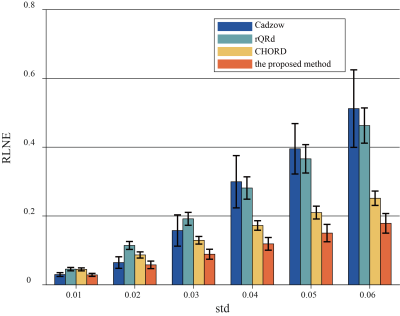
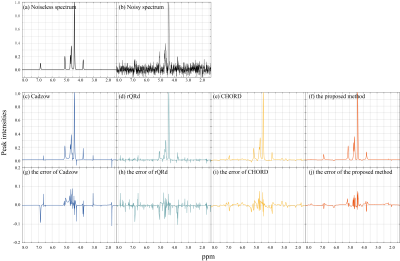
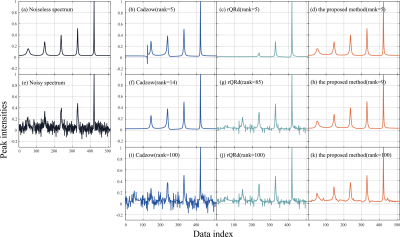
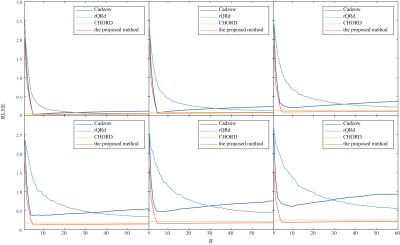
Denoised results of a synthetic data (σ = 0.020) is shown in Figure 1 with four different methods. Figure 2 displays the RLNEs of four methods under different noise levels on the synthetic data shown in Figure 1(a) in 100 Monte Carlo trials respectively. Figure 3 demonstrates the denoised results comparison on realistic metabolic data (σ = 0.050). The above three figures show that, compared with other mainstream NMR spectroscopy denoising methods, our proposed method has better denoising ability. Figure 4 and Figure 5 shows that, compared with other methods which require a priori on the number of exponentials, our method is more robust to this condition.

Conclusion

We proposed a model for denoising NMR spectroscopy signals based on exponential decomposition constraints, which takes full advantage of the low-rank properties and exponential structure of FID. Several different experiments show that compared with the state-of-the-art denoising methods, the proposed method has better denoising ability and is more robust to the set of the number of exponentials. In practical applications, the number of priori exponents can be set to 2-3 times the number of real exponents, which is relatively easy to estimate^17,18.

Acknowledgements

The correspondence should be sent to Prof. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)

References

[1] QIU T, WANG Z, LIU H, et al. Review and prospect: NMR spectroscopy denoising and reconstruction with low‐rank Hankel matrices and tensors [J]. 2021, 59(3): 324-45.

[2] WANG Z, GUO D, TU Z, et al. A sparse model-inspired deep thresholding network for exponential signal reconstruction--application in fast biological spectroscopy [J]. 2022.

[3] DONOHO D L, JOHNSTONE I M. Threshold selection for wavelet shrinkage of noisy data; proceedings of the Proceedings of 16th annual international conference of the IEEE engineering in medicine and biology society, F, 1994 [C]. IEEE.

[4] BROWN R G, HWANG P Y J I T R S, EXERCISES A K F W M, et al. Introduction to random signals and applied Kalman filtering: with MATLAB exercises and solutions [J]. 1997.

[5] MAN P P, BONHOMME C, BABONNEAU F J S S N M R. Denoising NMR time-domain signal by singular-value decomposition accelerated by graphics processing units [J]. 2014, 61: 28-34.

[6] CADZOW J A J I T O A, SPEECH,, PROCESSING S. Signal enhancement-a composite property mapping algorithm [J]. 1988, 36(1): 49-62.

[7] CONDAT L, HIRABAYASHI A J S T I S, PROCESSING I. Cadzow denoising upgraded: A new projection method for the recovery of Dirac pulses from noisy linear measurements [J]. 2015, 14(1): 17-47.

[8] HALKO N, MARTINSSON P-G, TROPP J A J S R. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions [J]. 2011, 53(2): 217-88.

[9] QIU T, LIAO W, HUANG Y, et al. An Automatic Denoising Method for NMR Spectroscopy Based on Low-Rank Hankel Model [J]. 2021, 70: 1-12.

[10] QU X, WU J. A Denoising Method of Magnetic Resonance Spectrum Based on Exponential Decomposition Constraint, CN114428222A [P/OL].

[11] KOEHL P J P I N M R S. Linear prediction spectral analysis of NMR data [J]. 1999, 34(3-4): 257-99.

[12] YING J, LU H, WEI Q, et al. Hankel matrix nuclear norm regularized tensor completion for N-dimensional exponential signals [J]. 2017, 65(14): 3702-17.

[13] QU X, HUANG Y, LU H, et al. Accelerated nuclear magnetic resonance spectroscopy with deep learning [J]. 2020, 132(26): 10383-6.

[14] YING J, CAI J-F, GUO D, et al. Vandermonde factorization of Hankel matrix for complex exponential signal recovery—application in fast NMR spectroscopy [J]. 2018, 66(21): 5520-33.

[15] GABAY D, MERCIER B J C, APPLICATIONS M W. A dual algorithm for the solution of nonlinear variational problems via finite element approximation [J]. 1976, 2(1): 17-40.

[16] GLOWINSKI R, MARROCO A J R F D A, INFORMATIQUE, RECHERCHE OPéRATIONNELLE. ANALYSE NUMéRIQUE. Sur l'approximation, par éléments finis d'ordre un, et la résolution, par pénalisation-dualité d'une classe de problèmes de Dirichlet non linéaires [J]. 1975, 9(R2): 41-76.

[17] MALINOWSKI E R J J O C A J O T C S. Abstract factor analysis of data with multiple sources of error and a modified Faber–Kowalski F‐test [J]. 1999, 13(2): 69-81.

[18] MELOUN M, ČAPEK J, MIKŠı́K P, et al. Critical comparison of methods predicting the number of components in spectroscopic data [J]. 2000, 423(1): 51-68.

Figures

Figure 1. Denoised results of a synthetic data with σ = 0.020 for four methods. Note: The results of Cadzow, rQRd and the proposed method that enable the lowest RLNE are presented here.

Figure 2. The RLNEs of four methods under different noise levels on synthetic data. The height of columns and vertical bars denote the average and the standard deviation of RLNEs in 100 Monte Carlo trials respectively.

Figure 3. Denoised results comparison on realistic metabolic data. The first rows denote the simulated data with and without noise (σ = 0.050) respectively. The second and third rows are the denoising spectra and its error of Cadzow, rQRd, CHORD and the proposed method, respectively. Note: The results of Cadzow , rQRd and the proposed method that enable the lowest RLNE are presented here.

Figure 4. Denoised results comparison on synthetic data. (a) and (e) denote the simulated data with and without noise (σ = 0.04) respectively. (b)-(d) are the denoising spectra of Cadzow, rQRd and the proposed method with R smaller than the optimal R. (f)-(f) are the denoising spectra of Cadzow, rQRd and the proposed method with optimal R. (i)-(k) are the denoising spectra of Cadzow, rQRd and the proposed method with R larger than the optimal R.

Figure 5. The average RLNEs of denoised results versus estimated R of the synthetic data over 100 Mont Carlo trials. The exact number of exponentials R is 5. (a)-(f) denote the average RLNES if denoised results with σ= 0.01, 0.02, 0.03, 0.04, 0.05, 0.06.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

4610

DOI: https://doi.org/10.58530/2023/4610