Synopsis

Keywords: RF Pulse Design & Fields, Brain

In the BSS method, WA and MLE as two methods in channel combination were proposed in |B1+| mapping for the multi-channel coils. We investigated the effects of the channel numbers on the performance of WA and MLE. The results showed the accuracy of |B1+| maps improved with the channel numbers increasing, even at low SNR. However, this trend slowed down when the channel numbers reached 24 or above. The RSD of WA and MLE was reduced to 6.6% and 4.0% for 24-channel coils, but the improvements were only 1.0% and 0.7% for 32-channel coils at SNR=25.

Introduction

The Bloch-Siegert shift (BSS) technique as a fast and precise B1 mapping approach ^[1], can be applied in RF shimming, correcting relaxation time ^[2] measurement and electrical property tomography ^[3]. As for array receive coils, previous studies have proposed several solutions to combine the individual channel BSS signal for retrieving |B1+| maps ^[4], such as the weighted averaging (WA) ^[5] and the maximum likelihood estimation (MLE) method ^[6]. As yet, the effects of channel numbers on the performance of WA and MLE need to be explored further. Here, based on the BSS approach, we have evaluated the effects of RF coil channel numbers on |B1+| mapping using the WA and MLE methods.

Methods

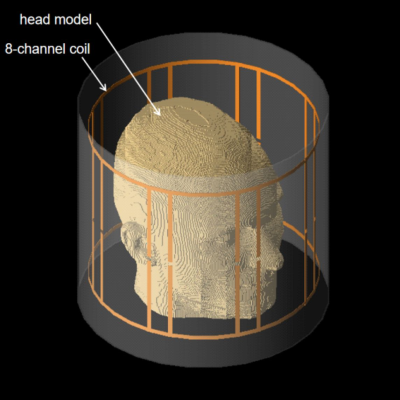
We set up six groups of coils with 6, 12, 16, 24, and 32 channels. Fig1 shows Duke’s head model and 8-channel coil configuration. At 3T, the transmit and receive field data are obtained by simulation via XFDTD (Remcom, State College, PA). The MR signal of each channel is synthesized by the BSS sequence signal expression.
$$\overline{\mathrm{S}}_{\mathrm{i}}^{+}=\mathrm{C} \cdot \tilde{\mathrm{B}}_{1,i}^{-}\cdot\frac{\left(1-\mathrm{e}^{-\frac{\mathrm{TR}}{\mathrm{T}_{1}}}\right) \cdot \sin (\theta)}{1-e^{-\frac{\mathrm{tr}}{\mathrm{T}_{1}}} \cdot \cos (\theta)} \cdot \mathrm{e}^{i \cdot\varphi } \cdot \mathrm{e}^{\mathrm{i} \cdot \mathrm{K}_{\mathrm{BS}}} \cdot\left|\mathrm{B}_{1, \operatorname{norm}}^{+}\right|^{2}$$
In addition, we set four sets of signal-to-noise ratios (SNR) of 200, 100, 50, 25 and a noise-free reference set. Gaussian noise is calculated according to the BSS signal inside the region of interest (ROI) and then added to each channel signal separately.
Then we combined the noise signals of an individual channel using WA and MLE methods to calculate the |B1+| map across all coil groups, respectively. The weighting factor of the WA method is the signal amplitude A_i, while the MLE method uses the square of the ratio of signal intensity to noise standard deviation ( A_i /σ_i)² as the weighting factor. Finally, the |B1+| maps of the six coils at different SNRs were compared with the noise-free reference set, and the relative standard deviation (RSD) was used to quantify the bias.
$$\mathrm{RSD}= 100 \%\times\sqrt{\sum_{\mathrm{i}=1}^{\mathrm{N}}\left(\left|\mathrm{B}_{1}^{+}\right|_{\mathrm{i}}-\overline{\mid \mathrm{B}_{1}^{+}} \mid\right)^{2} /(\mathrm{N}-1)} / \overline{|\mathrm{B}_{1}^{+} \mid}$$

Results

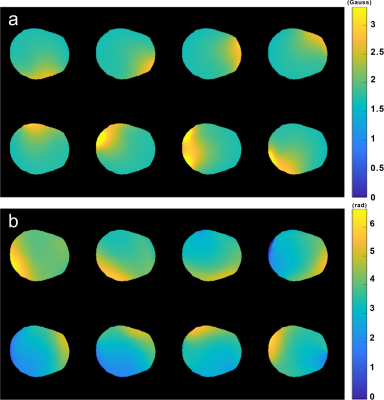
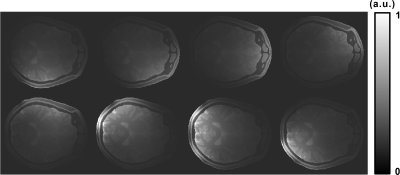
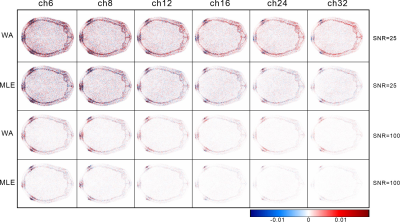
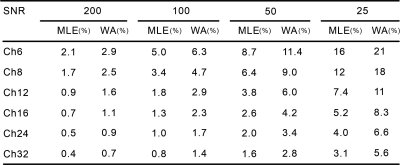
Fig2 shows the amplitude (a) and phase (b) results of the transmit field in an 8-channel receiver coil at SNR=∞. Fig3 displays the amplitude image of the BSS signal for each channel of the 8-channel coil. In Fig4, the |B1+| maps of six receive coils are exhibited by WA and MLE methods at SNR=25 and 100. With the number of channels increased, both weighting methods yielded low bias |B1+| maps, and the image of MLE is better than that of WA under the same channel numbers. The |B1+| maps bias of all coils are quantified as shown in Table1. When the SNR is greater than 200, the RSD of |B1+| maps obtained by WA and MLE methods in 32-channel and 6-channel coils are 2.1%, 0.4%, and 2.9%, 0.7% respectively, which are not significantly different. However, when SNR was reduced to 25, the RSD_WA and RSD_MLE of the 32-channel coil reached 5.6% and 3.1%, while those of the 6-channel coil reached 21% and 16%.

Discussion/Conclusion

The simulation of the 8-channel coil in this study was consistent with previous reports ^[6]. In the background of the BSS method, we grouped the number of coil channels and SNR to quantify the accuracy of the |B1+| map obtained by WA and MLE methods for coils with different channel numbers. Experiments show that the bias of the |B1+| map will reduce while the coil channel numbers increase. But the improvements in RSD_WA and RSD_MLE were only 1.0% and 0.7% for the 24-and 32-channel coils at SNR=25. We hope this study could provide a quantitative reference to figure out a balance of BSS performance, coil cost, and manufacture complexity.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 62271007, 82102742). The numerical calculations in this work have been done on the Medical Big Data Supercomputing Center System of Anhui Medical University.