4567

Subject Specific Prediction of Gradient-Induced E-fields Using a Multivariate Linear Modeling Approach

Koray Ertan¹, Peter B Roemer², and Brian Rutt¹
¹Radiology, Stanford University, Stanford, CA, United States, ²Roemer Consulting, Lutz, FL, United States

Synopsis

Keywords: Gradients, Gradients, PNS, Peripheral Nerve Stimulation, Safety, Bioeffects, Magnetic Fields

Peripheral Nerve Stimulation (PNS) remains as a limiting factor for gradient coils despite the recent advances. PNS thresholds varies significantly across population group. In this study, E-fields are simulated on simplified body model population with randomized realistic body dimensions and different patient landmark positions. It is shown that multivariate linear model with body dimensions and z-offset location as the independent variables can accurately predict the maximum E-field on the surface which can also be used to predict PNS thresholds. This simple multivariate model may pave the way to estimate subject specific PNS thresholds using simple anatomical measurements.

Introduction

Peripheral nerve stimulation (PNS) has become a significant limiting factor for high performance gradient coils, including latest generation head gradients.
E-field calculation using simplified body models is an accepted method for predicting PNS thresholds of both head and body gradient coils¹. Our previously introduced E-field calculation method was shown to predict population-mean experimental PNS measurements². We integrated this method into our gradient design code, demonstrating the ability to design PNS-optimal gradient coils^2,3.
Population-average PNS thresholds (either measured or calculated) are generally used on scanners to set safety limits. There may be significant advantages in being able to predict PNS thresholds rapidly and accurately for individual subjects, but this has not been achieved to date; for example, prior studies have not found significant correlations between PNS thresholds and anatomical measurements⁴.
Our computationally-efficient method of calculating E-fields on simplified body models with realistic head, neck and shoulder geometries allows us study E-field variations over large populations of body models, using realistic body dimensions drawn from established anthropomorphic databases5. The aim of the present work was to construct and test linear models for predicting maximum body surface E-field, E_max, which is known to correlate well with PNS thresholds^1,2. We trained and tested our models using populations of body models that spanned the full range of body dimensions and position offsets.

Methods

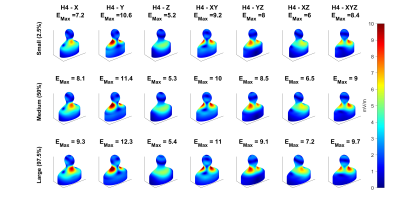
We analyzed two existing head gradient coils, one symmetric (H4) and one asymmetric (ESP)², which have significantly different field characteristics. B-field profiles were simulated in Sim4Life (ZMT MedTech AG, Zurich). E-fields were calculated on standardized body models with simplified geometry and uniform interior electrical properties; these included head, neck, shoulder, and torso regions as shown in Figure 1¹. We used our fast E-field calculation method to calculate E-fields and to extract maximum surface E-field per unit slew rate, E_max, over large populations of body models in which body dimensions were selected randomly from published adult male and female statistical distributions⁵. Nine relevant head/neck/shoulder dimensions were varied, initially in an independent fashion, to study the sensitivity of E_max to change in each parameter. Later, sets of 100 male and 100 female body models with random selection of all nine dimensions were generated for each coil and each axis. E-fields were calculated on the surface and E_max extracted. Additional random populations were placed at three different z-offsets (z=-2,0,2 cm) to study the effect of subject Z-location. For each gradient coil and axis, multivariate linear models were fit using body dimensions and z-offsets as the independent variables and E_max as the dependent variable. Populations were split in half for model training and testing.

Results

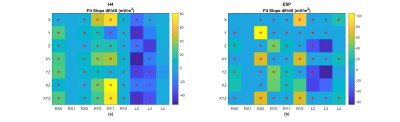
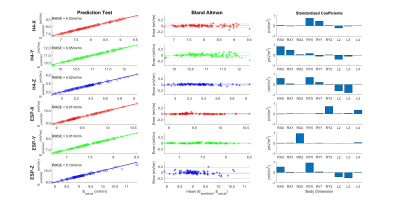
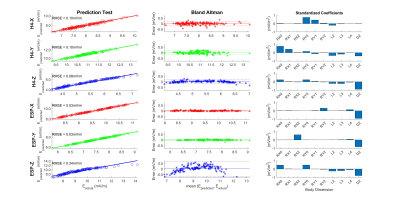
Figure 2 shows that E-field distributions vary significantly between small (2.5%ile), medium (50%ile) and large (97.5%ile) body models, with larger models typically showing higher values of E_max. The sensitivities of E_max to independent changes in each of the nine-dimension parameters (defined as the slope of E_max vs dimension) are shown in Figure 3. Results show both positive and negative sensitivities that vary significantly in strength and with dimension parameter for different gradient coils and axes. E_max varies highly linearly with each dimension (R²>0.95) except for ESP-XZ which exhibits some non-linearities. With this evidence of linearity, we then fit multivariate linear models using randomly selected training samples consisting of 50 male and 50 female models. We found that for all coils and axes, R² values for the multivariate fits exceeded 0.99. Additionally, the multivariate models were tested using independent randomly selected test samples, in all cases demonstrating highly accurate prediction of E_max (normalized RMSE<1% for all cases). Detailed results and analyses of multivariate linear models are shown in Figure 4. When subject Z-location (z-offset) was included in the training and test data, normalized RMSE slightly increased but remained less than 3.5% (Figure 5).

Discussion and Conclusion

Our results show that E_max is accurately predicted using multivariate linear models that only require knowledge of a few key body dimensions. Our prior work has shown that population PNS thresholds are accurately predicted (to within 20%) from population-averaged E_max and that this methodology adheres to IEC standards¹. We believe, therefore, that the present work demonstrates a practical pathway toward accurate subject-specific PNS threshold prediction using simple multivariate modeling.
We found that E_max varies by nearly 100% across the adult body model populations, and this variation corresponds well with the variation of PNS thresholds between subjects observed in experimental PNS studies^2,6,7. We hypothesize, therefore, that by estimating E_max for an individual, we will be able to predict that individual’s PNS thresholds with reasonable accuracy. This would allow the customization of PNS limits on the scanner to the individual subject, for the first time. The present work also shows that E_max can be calculated either by fast E-field calculation method if a body model is constructed to match the individual anatomy, or via simple linear models that require knowledge of only a few key dimensions. Future work will test this hypothesis, as well as extending the methodology to explore more complex body models⁸ and a wider range of gradient coils.

Acknowledgements

We acknowledge research support from the National Institutes of Health (NIH R01 EB025131 and NIH U01 EB025144). We acknowledge ZMT Zurich MedTech AG for their Sim4Science support.

References

[1] IEC, Medical electrical equipment – Part 2-33: Particular requirements for the basic safety and essential performance of magnetic resonance equipment for medical diagnosis. International Electrotechnical Commissioin 2015 60601-2-33 Edition 3.2.

[2] Roemer, Peter B., et al. "Electric field calculation and peripheral nerve stimulation prediction for head and body gradient coils." Magnetic Resonance in Medicine (2021).

[3] Roemer, Peter B., and Brian K. Rutt. "Minimum electric‐field gradient coil design: Theoretical limits and practical guidelines." Magnetic resonance in medicine 86.1 (2021): 569-580.

[4] Chronik, Blaine A., and Meena Ramachandran. "Simple anatomical measurements do not correlate significantly to individual peripheral nerve stimulation thresholds as measured in MRI gradient coils." Journal of Magnetic Resonance Imaging 17.6 (2003): 716-721.

[5] Diffrient, N., Tilley, A.R., and Bardagjy, J.C., Humanscale 1/2/3 Manual. Humanscale. 2017, Chicago, IL: IA Collaborative Ventures, LLC.

[6] Chronik, Blaine A., and Brian K. Rutt. "Simple linear formulation for magnetostimulation specific to MRI gradient coils." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 45.5 (2001): 916-919.

[7] Zhang, Beibei, et al. "Peripheral nerve stimulation properties of head and body gradient coils of various sizes." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 50.1 (2003): 50-58.

[8] Davids, Mathias, et al. "Predicting magneto-stimulation thresholds in the peripheral nervous system using realistic body models." Scientific reports 7.1 (2017): 1-14.

[9] Ertan, Koray, et al. "Comparison of Gradient Induced Peak E-fields on Simplified and Realistic Body Models." Proceedings of the 30th Annual Meeting of ISMRM, London, 2022.

Figures

Figure 1: Simplified homogeneous body model has 5 different sub-volumes such as top of the head (semi ellipsoid), neck-head transition ($$$R_x=((R_{x2} + R_{x1})/2 - (R_{x2} - R_{x1})cos((z-z_3)\pi/L_3)/2), R_y=((R_{y2} + R_{y1})/2 - (R_{y2} - R_{y1})cos((z-z_3)\pi/L_3)/2)$$$), body-neck transition ($$$R_x=((R_{x1} + R_{x0})/2 - (R_{x1} - R_{x0})cos((z-z_2)\pi/L_2)/2), R_y=((R_{y1} + R_{y0})/2 - (R_{y1} - R_{y0})cos((z-z_2)\pi/L_2)/2)$$$)

Figure 2: E-field simulations of H4 gradient coil. Simulations are performed for example small, medium, and large body models for three gradient axes and their combination. Each body dimension parameter was chosen as 2.5%, 50% and 97.5% percentile of the population distribution for small, medium and large body models respectively.

Figure 3: Estimated slopes of each body dimension parameter with respect to maximum E-field in the single variable linear fit results for (a) H4 and (b) ESP coils are shown. Slopes are color coded for each body dimension parameter and each gradient axes combination. Red asterisks (*) shows linear fit results with $$$R^2 > 0.95$$$

Figure 4: Multivariate linear model fit results on randomly generated test population for X, Y and Z gradient axes for both H4 and ESP coils. First column shows the comparison between actual E-fields and predicted E-fields. Solid lines show the x = y line. Second column shows the Bland Altman plots for each linear model. Mean error and ±1.96 standard deviation of the error is shown with solid and dashed lines respectively. Last column shows the standardized coefficients.

Figure 5: Multivariate linear model fit results on randomly generated test population for X, Y and Z gradient of H4 and ESP including both 0 and ± 2cm z-offset(DZ). First column shows the comparison of actual E-fields and predicted E-fields. Solid lines show the x = y line. Second column shows the Bland Altman plots for each linear model. Mean error and ±1.96 standard deviation of the error is shown with solid and dashed lines respectively. Last column shows the standardized coefficients.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

4567

DOI: https://doi.org/10.58530/2023/4567