Synopsis

Keywords: RF Pulse Design & Fields, RF Pulse Design & Fields

In this work, robust excitation pulses for ³¹P spectroscopy at 7T are designed by optimal control. The particular challenges of inhomogeneous RF field due to use of surface RF coils and broad bandwidth requirements due to the nature of ³¹P were addressed thoroughly. The optimized RF pulses show superior performance compared to adiabatic RF pulses during numerical simulations and phantom experiments. Application of the optimized RF pulses to T₁ prediction by dual angle method is the logical consequence.

Introduction

³¹P magnetization transfer (MT) spectroscopy is an extremely interesting method to study phosphate metabolites involved in ATP generation¹. Similar to imaging other X-nuclei rather than ¹H, investigating ³¹P comes with the drawback of a poor SNR and a lower gyromagnetic ratio. Therefore, even at field strengths of 7T or above, surface coils are used for transmit and receive. The inhomogeneities associated with surface coils during transmit are a particular challenge for the specific measurement protocol because in addition to the pronounced $$$B_1$$$ imperfections, robust excitation must be provided for the entire width of the broad spectrum. Adiabatic RF pulses^2,3, and in particular the class of BIR-4, could be used for excitation, but robustness to lower $$$B_1^+$$$ regions is limited and the implementation on the MR scanner is not trivial⁴. Robust RF pulse optimization for ¹H inversion pulses has shown to yield excellent results in terms of efficiency⁵. Here, we pose the extension to optimization of robust excitation pulses for ³¹P MT spectroscopy. The optimized RF pulses are compared to BIR-4 RF pulses numerically, and in phantom measurements on a 7T preclinical MR system.

Theory

An optimal control framework for the design of time minimal, $$${\Delta}B_0$$$ and $$$B_1^+$$$ robust, non-selective excitation pulses is introduced. Key factor is definition of a desired magnetization pattern$$M_{des}=(0,\sin\beta,\cos\beta)^T,$$with $$$\beta$$$ being the desired flip angle. Assuming $$$N_{B_1^+}$$$ discrete instances of $$$B_1^+$$$ scales and $$$N_{{\Delta}B_0}$$$ discrete instances of $$$B_0$$$ offsets results in ensemble formulation of the cost functional through$$\underset{r,\varphi,\varepsilon,T_p}{min}J=\varepsilon+T_p+\frac{\alpha}{2}\int\limits_0^{T_p}\left(r^2(t)+\varphi^2(t)\right)dt+\frac{\mu}{p}\sum\limits_{i=1}^{N_{B_1^+}}\sum\limits_{j=1}^{N_{{\Delta}B_0}} \left(\frac{M_{des}-M_{i,j}(T_p)}{\varepsilon}\right)^p\\ \begin{cases}\frac{dM_{i,j}(t)}{dt}=A_{i,j}(t)M_{i,j}(t)+b,\\M_{i,j}(0)=(0,0,1)^T,\quad{\forall}~i=1,{\cdots}N_{B_1^+},\quad{\forall}~j=1,{\cdots}N_{{\Delta}B_0},\quad{\forall}t\in{\lbrack}0,T_p\rbrack,\\0~{\leq}~r(t)~{\leq}~r_{max},{\quad}0\leq\varphi(t)<2\pi.\end{cases}$$Therein, $$$T_p>0$$$ is the pulse duration and $$$\varepsilon>0$$$ the gap to the desired magnetization. $$$L^2$$$-regularization of the amplitude $$$r$$$ of the RF and the phase $$$\varphi$$$ is conducted with parameter $$$\alpha>0$$$. Flip angle accuracy is guaranteed within the last term in $$$J$$$, whereby an $$$L^p$$$-norm with $$$p{\geq}2$$$, $$$p$$$ even, is applied (penalization parameter $$$\mu>0$$$). In addition, the Bloch equations are solved for all instances of $$$B_1^+$$$ and $$${\Delta}B_0$$$ via symmetric operator splitting⁶. The inequalities facilitate box constraints on the RF pulse. The optimization is done with a trust-region semi-smooth quasi-Newton method⁷, whereby exact discrete derivatives are supplied by adjoint calculus⁸. Time minimization is conducted via a bi-level method.

Methods

The optimization was carried out in MATLAB (The Mathworks Inc., Natick, USA). Excitation pulses with flip angles of $$$15^\circ$$$ and $$$60^\circ$$$ were optimized, initialized with the corresponding BIR-4 pulses⁹. We set $$$r_{max}=500~\mu T$$$, and $$$B_1^+$$$ robustness was aimed for a scale of $$$40~\%$$$ to $$$120~\%$$$ (because of the coil's relevant sensitivity range) of the nominal amplitude in $$$N_{B_1^+}=81$$$ steps. $$$B_0$$$ robustness was aimed for $$$\pm15~{ppm}$$$, corresponding to bandwidth requirements of ³¹P, in $$$N_{{\Delta}B_0}=101$$$ steps. Within optimization, we chose $$$B_0=7~T$$$ and the gyromagnetic ratio $$$\frac{\gamma}{2\pi}=17.235~\frac{{MHz}}{{T}}$$$. For all investigated RF pulses, the time step size was $$$\tau=0.0024~ms$$$.
The optimal control pulses OC and the BIR-4 pulses were implemented on a 7T Bruker system (Biospec 70/20) within a gradient echo sequence, replacing traditional excitation pulses therein. In addition, GRE measurements with system-implemented SLR pulses with flip angles of $$$15^\circ$$$ and $$$60^\circ$$$ were performed for comparison. Phantom scans were acquired with a custom build surface coil (diameter $$$11~mm$$$) for transmit and receive. A slice phantom was created using a $$$5~ml$$$ syringe (diameter $$$12.3~mm$$$) and $$$475~\mu{l}$$$ of $$$98~\%$$$ ortho-phosphoric acid (slice thickness $$$4~mm$$$). The sequence parameters were set to $$$FOV=20\times 20~mm$$$, $$$matrix=64{\times}64$$$ and $$$TE~/~TR=2~ms~/~10~s$$$.To investigate performance regarding $$$B_1^+$$$ and $$${\Delta}B_0$$$ imperfections, we kept $$${\Delta}B_0$$$ fixed with $$$0~ppm$$$ and varied $$$B_1^+$$$ on purpose from $$$20~\%$$$ to $$$140~\%$$$. Vice versa, we set $$$B_1^+=100~\%$$$ and varied $$${\Delta}B_0$$$ for $$${\pm}19~ppm$$$ by implicitly changing the carrier frequency of the RF pulses¹⁰. A double angle $$$B_1^+$$$ map¹¹ was acquired to gather regions with same $$$B_1^+$$$, coil sensitivities were estimated on the basis of these measurements.

Results and Discussion

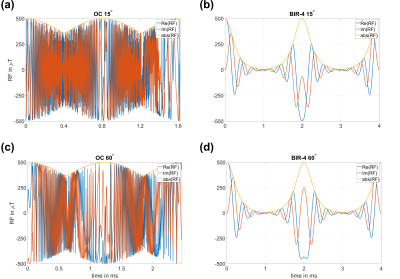
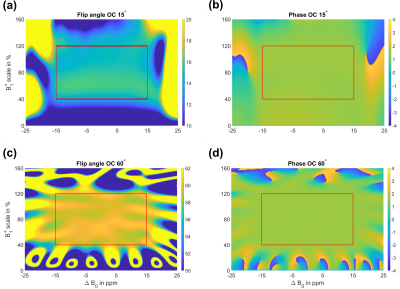
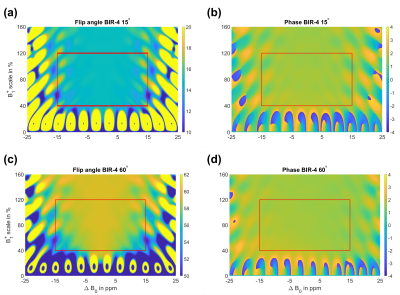
The optimized RF pulses OC$$$~15^\circ$$$ and OC$$$~60^\circ$$$ show a substantially reduced pulse duration (Figure 1), however, at the cost of an increased power integral ($$$PI_{OC,15}=3.2e5$$$ vs. $$$PI_{BIR-4,15}=1.8e5$$$ and $$$PI_{OC,60}=5.0e5$$$ vs. $$$PI_{BIR-4,60}=1.8e5$$$).
Numerical simulations revealed that OC$$$~15^\circ$$$ and OC$$$~60^\circ$$$ result in an even flip angle profile within the optimized region (Figure 2). Compared to the corresponding BIR-4 RF pulses (Figure 3), improvement in flip angle accuracy is especially observed in higher $$${\Delta}B_0$$$ regions. In addition, the phase profiles of OC are substantially smoother than with BIR-4 which is favored. For both OC pulses, less outliers are observed in flip angle and phase within the red boxes.
In phantom measurements, the superior performance of the OC pulses is observed in Figure 4. Both BIR-4 pulses result in the real experiment in inferior performance as expected from numerical simulations (Figure 3). This is a commonly known disadvantage of the BIR-4 class, arising from the phase jumps where the RF amplitude is zero⁴. The system-built in SLR RF pulses result in an exact flip angle at the region with ($$$B_1^+=100~\%$$$, $$${\Delta}B_0=0~ppm$$$), but worse performance anywhere else.

Conclusion and Outlook

$$$15^\circ$$$ and $$$60^\circ$$$ RF pulses for ³¹P spectroscopy were designed by optimal control, resulting in excellent performance for a broad range of $$$B_1^+$$$ imperfections and resonance offsets. This was verified in extensive numerical simulations, and phantom measurements with additional comparison to adiabatic RF pulses. A logical consequence of the presented work is application of the OC pulses to $$$T_1$$$ mapping by a fast dual-angle method¹².

Acknowledgements

No acknowledgement found.