4433
Simple Method for Bloch-Siegert B1 Map Data Processing
Andrew J Wheaton1 and Wayne R Dannels1
1Canon Medical Research USA, Mayfield, OH, United States
1Canon Medical Research USA, Mayfield, OH, United States
Synopsis
Keywords: System Imperfections: Measurement & Correction, System Imperfections: Measurement & Correction, B1 mapping
A simple data processing method for calculating B1 map data using the Bloch-Siegert shift method is described. The proposed method uses a phase conjugate approach instead of conventional phase subtraction. The proposed method has the dual advantages of 1) not requiring phase unwrapping and 2) enabling simple and SNR-efficient complex data combination for multi-channel phased array coils. One consequence of using a phase conjugate approach is a reduced range of resolvable B1 due to phase aliasing. A practical solution is offered to resolve this problem by making an assumption of the realistic range of expected B1.INTRODUCTION
Bloch-Siegert shift (BSS) is an efficient method of B1 mapping and RF transmit power calibration [1,2]. The BSS method typically follows these steps, in brief:- Acquire two datasets with BSS RF pulse at ±ωoffset: k1 and k2
- For each receive channel, compute complex images: i1 = ifft(k1) and i2 = ifft(k2)
- Combine complex receiver channel data using inverse receiver phase map P† of each channel q: I1 = Σi1,q*P†q and I2 = Σi2,q*P†q
- Compute phase images of the channel-combined datasets: θ1 = atan2(Im(I1),Re(I1)) and θ2 = atan2(Im(I2),Re(I2))
- Compute B1 map = sqrt((θ1 – θ2) / 2KBS) where KBS is the numerically computed constant for the BSS RF waveform [3]
Due to background ∆B0, phase ambiguity can occur in θ1 and θ2. One practical approach to resolving this phase ambiguity is to unwrap θ1 and θ2. In this abstract, we offer a BSS processing method which does not need phase unwrapping. The method is also suitable for combining multiple channels of a phased array coil without knowledge of the phase data of each receiver channel. We also offer a practical solution to resolving B1 ambiguity when the BSS-induced phase difference exceeds 2π.
METHODS
The proposed BSS processing method consists of the following steps:- Acquire two datasets with BSS RF pulse at ±ωoffset: k1 and k2
- Compute complex images: i1 = ifft(k1) and i2 = ifft(k2)
- For each channel, multiply i1 by the complex conjugate of i2: d = i1*conj(i2). This is equivalent to d = A1e(jθ1) * A2e(-jθ2) = A1A2e(j(θ1 – θ2)).
- Combine data from all channels q by simply adding complex d across all channels: D = Σdq
- Compute phase difference map ∆θ = atan2(Im(D),Re(D))
- Compute B1 map = sqrt(∆θ / 2KBS)
The key insight of the proposed method is that absolute phase (θ1 and θ2) does not need to be known to compute the B1 map. BSS only needs the phase difference ∆θ = θ2 – θ1 at each pixel. By leveraging the complex conjugate instead of subtraction of phase images, we can compute the phase difference easily without the need to phase unwrap θ1 and θ2. An added benefit is that the complex datasets dq can be simply added across channels to create the channel combined D without requiring an estimate of Pq. The complex data summation in this manner is also SNR-optimal, with magnitude-squared channel weighting analogous to the sum-of-squares method in tradition magnitude coil combination.
To demonstrate the proposed BSS processing method, data were acquired on a head of a human volunteer using a field-echo based BSS sequence on a 3T Canon Galan scanner under IRB approval. Scan parameters include: target B1 = 7uT, matrix = 128x128, TR = 60ms, flip=20°. A Fermi RF pulse with 8ms duration and ±4kHz frequency offset was used. Data acquisition was repeated using whole body coil (WBC) as the receiver and a 16-channel Head-Neck phased array coil (PAC). The performance of the proposed BSS method was compared to the conventional method.
RESULTS
The phase maps θ1 and θ2 are displayed in Figure 1. In this volunteer, modest phase unwrapping was necessary to execute the conventional processing method. The B1 map processed with the conventional method and proposed method are equivalent as demonstrated in Figure 2, highlighting the ability of the proposed method to accurately compute the B1 map without the need for phase unwrapping.The ability to combine channels using the simple complex summation is demonstrated in Figure 3. Without any knowledge of the phase data of the multi-channel PAC coil (Pq), the data can be channel-combined to create the correct B1 map.
DISCUSSION
For any BSS method, if B1 amplitude is sufficiently high so that the BSS-induced phase difference exceeds 2π, phase aliasing will occur. As a result, the estimate of B1 will be incorrect. With the phase conjugate approach, the phase subtraction is executed (via conjugate multiplication) before the arctangent operation. The conventional subtraction approach computes arctangent separately for θ1 and θ2. Therefore, the resolvable range of B1 before this 2π phase aliasing error occurs is reduced. The effect is illustrated in Figure 4.To solve this problem, we can leverage knowledge of the expected range of B1. But making an estimate of the lowest expected B1, we can calculate the smallest phase difference we should expect to measure: ∆θmin = KBS*B1min2. If the calculated phase is less than ∆θmin, we can be certain this measurement is aliased and we can correct it. The correction can be written as:
if (∆θ < ∆θmin), ∆θ += 2π*ceil((∆θmin - ∆θ) / 2π)
The effect of this correction can be observed in Figure 5. If we can safely make the assumption that minimum B1 is some percentage of expected B1, we can resolve a larger range of B1 correctly.
CONCLUSION
The proposed method for BSS data processing avoids the need for phase unwrapping and enables simple complex channel combination. It could be a practical method to help streamline the calculation of BSS B1 maps.Acknowledgements
No acknowledgement found.References
- Sacolick L, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert shift. MRM 2010; 63: 1315-1322.
- Sacolick L, Sun L, Vogel MW, Dixon WT, Hancu I. Fast radiofrequency flip angle calibration by Bloch-Siegert shift. MRM 2011; 66: 1333-1338.
- Basse-Lusebrink TC, Sturm VJF, Kampf T, Stoll G, Jakob PM. Fast CPMG-based Bloch-Siegert B1+ mapping. MRM 2012; 67: 405-418.
Figures

FIGURE 1: θ1
and θ2
maps of the human volunteer. Phase wrap is observed on left side and near
sinus.
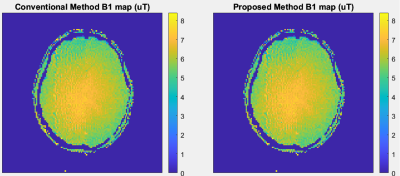
FIGURE 2: Comparison of
data processed using conventional BSS processing and the proposed method. Both
maps were acquired with single channel whole body coil receive. The B1 maps are
equivalent.
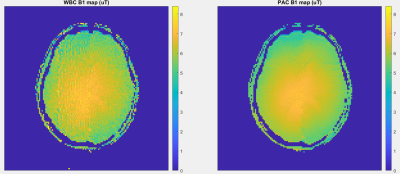
FIGURE 3: Comparison of B1
maps acquired using single channel whole body coil receive (WBC) and phase
array receiver coil (PAC) using the proposed simple channel combination method.
The B1 amplitude is expressed in microtesla (uT). The B1 maps are equivalent, except the SNR
of the PAC data is higher, as expected.
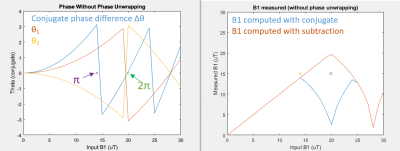
FIGURE 4: Example of B1 calculation error due to
phase alias. The proposed conjugate phase method reaches its alias point at
approximately 14uT (marked by the π) compared to the conventional phase
subtraction method which reaches its phase alias point at approximately 20uT.
The effect is to cause an error in B1 calculation due to phase aliasing.
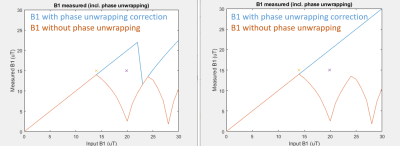
FIGURE 5: Examples of increasing the effective range of
resolveable B1 by incorporating an estimate of the minimum expected B1. If we
can assume B1 minimum is 50% of expected B1, the phase conjugate method can
increase its effective B1 range from 14uT to 22uT. If we can tighten our range
of expected B1, and assume minimum B1 is 80% of expected B1, the effective
range of resolvable B1 can increase to 30uT.
DOI: https://doi.org/10.58530/2023/4433