4426
Experimental and theoretical investigation of eddy current heating of RF shield in a high-performance gradient system1Radiology, Mayo Clinic, Rochester, MN, United States, 2GE Global Research, Niskayuna, NY, United States
Synopsis
Keywords: Gradients, Gradients, Eddy current heating
With a high-performance gradient system, gradient-induced eddy current in the RF shield can cause a substantial temperature rise in the patient bore. Especially, a multi-echo EPI sequence involving intense gradient switching and long echo trains, usually lasts for >10 minutes in many resting-state functional MRI studies. The temperature change caused by RF shield heating can jeopardize patient safety and hardware reliability. Based on theoretical and experimental investigation, we demonstrated two main factors that could contribute to the RF shield heating in a high-performance compact 3T scanner, namely the shield surface conductivity and mean-square slew rate of the gradient waveform.Introduction
Multi-echo EPI is a promising technique for resting-state functional MRI due to increased sensitivity by noise and artifact reduction through using multiple-TE images [1,2]. A high-performance head gradient coil in conjunction with a large acceleration factor enables high-spatial-temporal-resolution multi-echo EPI for whole brain functional mapping with substantially reduced geometric distortion [3-6].However, fast gradient switching combined with a high duty cycle (2~3 times higher than single-echo EPI) and prolonged (~10 min) scan time can cause increased eddy-current heating of the conductive RF shield located close to the gradient coil. Such heating can potentially pose a patient safety risk and thereby limit the allowable gradient duty cycle, reducing the benefit of a high-performance system.
Previous work has suggested eddy current reduction through novel materials and shield designs [7], but quantitative investigation of the heating as a function of the material properties and gradient waveform parameters has not been published. Here we address this problem using two RF shield assemblies in a compact 3T (C3T) [8] scanner with high-performance gradient system and demonstrate factors to influence heating with practical multi-echo EPI sequences.
Theory
A thin, continuous conductive cylindrical shell that lines the gradient coils inner diameter was applied as the RF shield. Systematic dimensional analysis using linear algebraic methods [9] determines the power law dependence of the eddy-current heating power $$$P$$$ in units [W] of the RF shield with relevant experimental variables, namely the surface conductivity $$$σ_s$$$ [S] and radius $$$a$$$ [m] of the shield, and the amplitude $$$G$$$ [mT/m] and slew rate $$$SR$$$ [T/m/s] of the gradient waveform. Decomposing their units into the fundamental units [m], [kg], [s], [A], we obtain a dimensional matrix $$$D$$$ (Fig. 1). The equation $$$De=0$$$ yields a unique solution which states that for a given geometry, $$$P$$$ is proportional to the surface conductivity, radius to the sixth power, and the square of the slew rate. Note the absence of gradient amplitude dependence (see Discussion). This analysis agrees with a more detailed power equation that can be derived from the surface eddy current theory [10]. Our analysis suggests that the shield heating primarily depends on (i) the surface conductivity of the shield material and (ii) the mean square slew rate of the gradient waveform.Material and Method
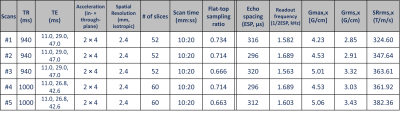
All experiments were performed on the C3T scanner with a high-performance gradient coil rated at 80 mT/m and 700 T/m/s [8].We used a multi-band, multi-echo EPI sequence that is part of our routine research fMRI protocol with a few variations in ramp sampling ratio to enable adjustment of $$$SR_{rms}$$$. The sequence parameters are given in Table 1. The readout direction was x (left/right). Gradient waveform parameters including the echo spacing (ESP), $$$G_{rms}$$$ and $$$SR_{rms}$$$ were evaluated from waveform data files saved on the scanner's host computer upon sequence download.
Two insertable RF shield assemblies, referred to as "original" and "new" shields, with different shield conductivities were tested. The new shield was estimated to have one half of the surface conductivity of the original one. Both assemblies included an integrated 16-rung birdcage coil (with identical design) for RF transmission and reception.
For each EPI sequence, a thermal imaging camera (FLIR C2, Flir Systems AB, Sweden) was employed to capture surface temperature maps in the scanner bore at baseline,6,8,10 minutes into the scan. A cooldown time of 15 minutes was sufficient to bring the bore temperature back to the baseline between the scans.
Results
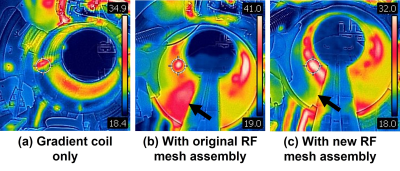
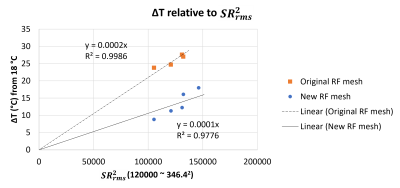
Figure 2 shows examples of surface thermal images obtained after 10 minutes of scan with pulse sequence #2 in Table 1. With the original RF shield assembly, the peak surface temperature was 42.7°C, much higher than that of the bare gradient coil (32.2°C). The scanner bore with the new RF shield showed a much lower peak temperature (34.1°C). The area of the elevated temperature near the bottom of the bore dramatically decreased with the new RF shield as indicated. The hot spots for the new shield were more localized, indicating that eddy current heating was dominated by the heating of copper rungs in the birdcage coil.Figure 3 shows a plot of $$$∆T$$$ as a function of $$$SR_{rms}^2$$$ for the two RF shields. Approximate proportional relationship between $$$∆T$$$ and $$$SR_{rms}^2$$$ was observed. The slopes of the linear fit lines differed by about 2, consistent with the surface conductivity ratio of the shields.
Correlation analysis showed that $$$SR_{rms}^2$$$ had a higher correlation coefficient (0.93) with $$$∆T$$$ than $$$G_{rms}^2$$$ (0.86) or $$$f_{ESP}^2G_{max}^2$$$ (0.82) averaged over all data.
Discussion and Conclusion
Through dimensional analysis and experimental demonstration, we identified two main factors affecting the bore temperature rise in the C3T scanner, namely shield surface conductivity and mean-square $$$SR$$$ of the readout gradient waveform.The absence of gradient amplitude $$$G$$$ in the solution means it is dimensionally irrelevant [11]. However, in the important special case of sinusoidal driving, which is often convenient for taking measurements, $$G(t)=G_0cos(ωt)$$ the solution can alternatively be expressed in terms of gradient amplitude × angular frequency, because $$$SR_{rms}=(ωG_0)/\sqrt{2}$$$.
Limitations of our investigation include: (1) assumption of homogeneous shield, ignoring local features such as joints and seams, (2) indirect shield heating measurement through bore surface temperatures, and (3) lack of independent control of air cooling.
Acknowledgements
This work was supported by NIH grant U01-EB024450 and U01-EB026979. This presentation does not necessarily represent the official views of NIH.References
1. Poser, B.a., et al., BOLD contrast sensitivity enhancement and artifact reduction with multiecho EPI: Parallel-acquired inhomogeneity-desensitized fMRI. Magnetic Resonance in Medicine, 2006. 55(6): p. 1227-1235.
2. Kundu, P., et al., Differentiating BOLD and non-BOLD signals in fMRI time series using multi-echo EPI. NeuroImage, 2012. 60(3): p. 1759-1770.
3. Kang, D., et al., The benefit of high-performance gradients on echo planar imaging for BOLD-based resting-state functional MRI. Phys Med Biol, 2020. 65(23): p. 235024.
4. Kang, D., et al. Feasibility of high spatial and temporal resolution multi-echo multi-band whole brain resting-state functional MRI on a compact 3T system. in Proc. Intl. Soc. Mag. Reson. Med. 2020.
5. Kang, D., et al. Potential Benefit of Multiband Multiecho EPI for Resting-state Functional MRI in Alzheimer's disease on a compact 3T system: A Preliminary study. in Proc. Intl. Soc. Mag. Reson. Med. . 2021.
6. Kang, D., et al. Benefits of echo combination for high-spatial-resolution ME resting state FMRI on a compact 3T scanner. in Proc. Intl. Soc. Mag. Reson. Med. . 2022.
7. Rosler, M.B., et al., A transmit-receive array for brain imaging with a high-performance gradient insert. Magn Reson Med, 2020. 84(4): p. 2278-2289.
8. Foo, T.K.F., et al., Lightweight, compact, and high-performance 3T MR system for imaging the brain and extremities. Magn Reson Med, 2018. 80(5): p. 2232-2245.
9. Lee, S.K. and M.A. Bernstein, Systematic Dimensional Analysis of the Scaling Relationship for Gradient and Shim Coil Design Parameters. Magn Reson Med, 2022. 88(4): p. 1901-1911.
10. Lee, S.-K., et al. Analytical approach towards time-dependent gradient eddy current calculation in cylindrical geometry. in 29th Annual Meeting of ESMRMB. 2012. Lisbon, Portugal.
11. Bernstein, M.A. and W.A. Friedman, Thinking About Equations: A Practical Guide for Developing Mathematical Intuition in the Physical Sciences and Engineering. 2009, Hoboken, NJ: Wiley.
Figures