4425
Robust RF Shimming With Minibatched Magnitude Least Squares Optimization
Jonathan B Martin1 and William A Grissom2
1Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2Vanderbilt University, Nashville, TN, United States
1Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2Vanderbilt University, Nashville, TN, United States
Synopsis
Keywords: RF Pulse Design & Fields, High-Field MRI
We present a magnitude-least-squares RF shimming algorithm which uses interleaved noisy and locally converging updates to escape local minima and find low-cost shim solutions. We introduce noise in the algorithm by performing updates using a small minibatch of the available B1+ measurements. The method is validated using in-vivo head B1+ maps from a 7T scanner. An optimal minibatch size is found which consistently produces low-power and low-RMSE solutions across subjects and through head slices. This shim design method may be employed to more robustly correct for B1+ inhomogeneities at ultra-high field strengths than is possible with conventional methods.Introduction
B1+ inhomogeneity severely impacts image quality at ultra-high field strengths1-2. One approach to mitigating RF inhomogeneity is RF shimming3, in which the static driving magnitude and phase of the elements in a multi-channel coil array is optimized. RF shims are often patient-tailored and may be independently designed for each slice in a 2D acquisition scheme, to correct varying transmit field inhomogeneities. Framing shim design as a magnitude least-squares (MLS) optimization problem provides advantages over other formulations for the purposes of maximizing homogeneity of the magnitude of B1+4-5. However, the MLS optimization problem is non-convex, and thus iterative shimming algorithms are prone to stalling in local minima rather than returning globally optimal shim solutions5-6.These local minima often manifest as large signal nulls in the shim solution, which substantially degrade image quality7.In order to successfully prevent stalling in local minima during optimization, we propose a minibatched MLS optimization algorithm. The algorithm alternates between global exploration of the loss landscape using a noisy update, and local convergence using the conventional Gerchberg-Saxton (GS) method6. We introduce noise in the GS algorithm by performing updates using a small minibatch of the available B1+ measurements. In this work, we apply this algorithm to the 7T slice-by-slice RF shimming problem for brain imaging.
Algorithm
Figure 1 shows a pseudocode outline of the proposed algorithm (Algorithm 2). The algorithm is a modification of the Gerchberg-Saxton or variable exchange method6 (Algorithm 1), which explicitly splits the RF shim’s magnitude and phase contributions x and $$$\phi$$$ and alternates between updating each. Similarly, this procedure is followed in the proposed Algorithm 2, but in this method a noisy update is performed every n iterations to help the algorithm escape local minima. Noise is introduced in these iterations by performing the GS update with $$$\tilde{A_i}$$$, the Ns x Nc RF shimming pTx system matrix subsampled in the row (spatial) dimension. Rows are sampled with uniform probability across all spatial locations within the masked slice to form the minibatched system matrix. A fixed number of iterations is performed, and the RF shim providing the lowest overall cost is returned.Methods
Whole-brain B1+ maps were acquired in two healthy subjects (Subject 1 = 25 y.o. F, Subject 2 = 24 y.o. M) on a Philips 7T Achieva (Philips Healthcare, Best, Netherlands), using a Nova 8Tx/32Rx head coil and a multislice 2D DREAM acquisition (3.5 mm3 isotropic resolution, 224 x 224 x 154 mm3 FOV, 44 axial slices)6. Brain extraction and B1+ map calculation were performed using MRCodeTool (MR Code, Zaltbommel, the Netherlands).Each slice was shimmed using batch GS optimization and the proposed minibatched algorithm (n=3 interleaved batch GS steps) for 500 iterations in 20 trials. Slices with fewer than 500 pixels in the brain were excluded from shimming. Optimization was repeated across a range of power regularization values to form a FA error/RF power L-curve, and for minibatch sizes N = [1:1:100] rows per minibatch. Both methods were initialized with a quadrature B1+ phase. The proposed algorithm was also compared to a random exploration method, in which 500//4 random initializers were generated and refined with n=3 batch GS steps to match the computational budget and structure of the proposed algorithm.
Results
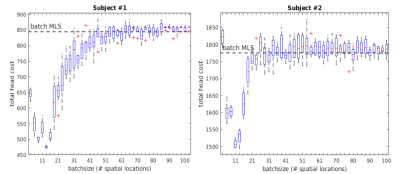
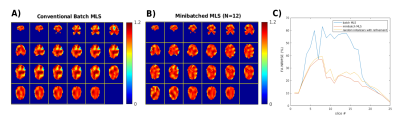
Figure 2 shows the total cost summed across all slices for minibatched MLS over the range of minibatch sizes investigated. In both heads, there is a minimum in shim error at small minibatch sizes, centered around a minibatch size of N = 12 rows. As minibatch sizes grow larger, the performance of the algorithm converges to that of batch MLS/conventional GS. At very small minibach sizes of less than 4 rows, error increases as the minibatched updates becomes numerically unstable.Figures 3a and 3b show by-slice results of the batch and minibatch MLS shimming algorithms in subject 1. The minibatched MLS result uses the optimal minibatch size of N = 12 rows; slices shown are those with the median error across trials. The local minima which quadrature-phase initialized batch MLS converges can be avoided by using minibatched MLS. Figure 3c shows the mean NRMSE error by slice. Minibatching outperforms both batch MLS and random initialization with refinement across the head.
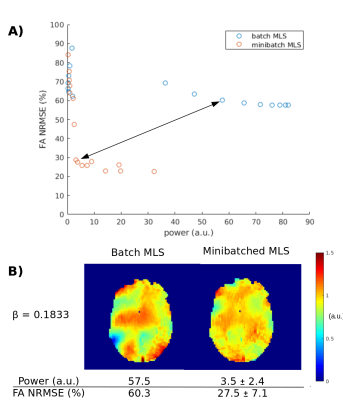
Figure 4 shows the L-curves for slice 12 of subject 1. The set of solutions that minibatched MLS generates show both substantially decreased RF power and FA NRMSE. The median minibatch solution shown in Figure 4b is much more homogeneous with lower power than the equivalent batch MLS solution.
Discussion and Conclusion
Minibatched MLS robustly produces RF shimming solutions with lower error than full batch MLS in the head, and produces less error with lower power than the random exploration method. With a minibatch size of 12 rows, shimming performance was improved across all slices throughout the head.The method can be combined with power regularization, and the resulting trade-off between excitation error and RF power is more favorable than that provided by conventional MLS. Future work includes extending the algorithm to multi-spoke pTx pulse design, along with additional anatomies and coil profiles.Acknowledgements
This work was supported by NIH grant R01 EB016695.References
1.M. Alecci, C. M. Collins, M. B. Smith, and P. Jezzard, Radio frequency magnetic field mapping of a 3 Tesla birdcage coil: experimental and theoretical dependence on sample properties, Magn Reson Med, 2001; 46(2): 379–385.
2. Q. X. Yang, J. Wang, X. Zhang, C. M. Collins, M. B. Smith, H. Liu, X. H. Zhu, J. T. Vaughan, K. Ugurbil,and W. Chen, Analysis of wave behavior in lossy dielectric samples at high field, Magn Reson Med 2002; 47(5): 908-915.
3. J. Ellermann, U. Goerke, P. Morgan, K. Ugurbil, J. Tian, S. Schmitter, T. Vaughan, and P.-F. Van De Moortele, “Simultaneous bilateral hip joint imaging at 7 Tesla using fast transmit B1 shimming methods and multichannel transmission– a feasibility study,” NMR Biomed. 2012; 25(10): 1202– 1208.
4. Setsompop K, Wald LL, Alagappan V, Gagoski BA, Adalsteinsson E.Magnitude least squares optimization for parallel radio frequencyexcitation design demonstrated at 7 Tesla With Eight Channels. Magn Reson Med. 2008; 59(4): 908-915.
5. A. Hoyos-Idrobo, P. Weiss, A. Massire, A. Amadon, and N. Boulant, On variant strategies to solve the magnitude least squares optimization problem in parallel transmission pulse design and under strict sar and power constraints, IEEE TMI 2014; 33(3): 739–748.
6. P. W. Kassakian, “Convex approximation and optimization with applications in magnitude filter design and radiation pattern synthesis,” Ph.D. dissertation, University of California, Berkeley, 2006.
7. A. Paez, C. Gu, and Z. Cao, Robust RF shimming and small-tip-angle multispoke pulse design with finite-difference regularization, Magn Reson Med 2021; 86(3): 1472–1481.
Figures
Figure 1. A) Conventional Gerchberg-Saxton MLS optimization, and the proposed algorithm. Unlike conventional GS optimization, the proposed algorithm alternates between using the full pTx system matrix A and a system matrix $$$\tilde{A_i}$$$ formed from a minibatch of spatial locations. B) The minibatching procedure is shown. The full Ns x Nc system matrix $$$A$$$ is masked with a random row sampling vector, which is produced by a random uniform sampling in space across the masked brain slice.
Figure 2. Minibatched MLS performance over minibatch sizes, in two human heads. The total head cost is minimized in both subjects with a minibatch size of approximately N=12 rows. Cost quickly increases with increasing batchsize, and converges to the cost of full batch MLS optimization. In the case of very small minibatch sizes, N<5, error begins to increase as the minibatch updates cause error to increase substantially. For N<3, error diverges for a large number of slices, and total cost is not shown.
Figure 3. (A-B) By-slice shimming results without power regularization, for subject 1. B) shows the minibatched MLS slice solutions for the shimming trial with median whole-head error. Minibatched MLS produces shim solutions that are more homogeneous, with fewer signal nulls than batch MLS. C) Mean flip angle error by slice for batch MLS, minibatched MLS, and the random initialization with refinement. Minibatched MLS has lower average error across the entire head.
Figure 4. A) L- curves for RF shimming of slice 12 in subject 1. The arrow shows the shim solutions using the same regularization value. These solutions are plotted in B). B) Magnitude shim for $$$\beta$$$ = 0.1833 designed by batch MLS and minibatched MLS; median total error minibatch solution is shown. The minibatched solutions have substantially lower power and error than the batch MLS solution.
DOI: https://doi.org/10.58530/2023/4425