4421
On the spatiotemporal phase modulation of odd and even EPI echoes at 300 mT/m diffusion MRI: A field monitoring analysis
Gabriel Ramos Llorden1, Daniel Park1, Hong-Hsi Lee1, Alina Scholz2, Boris Keil2, Lawrence L. Wald1,3, Thomas L. Witzel4, and Susie Y. Huang1,3
1Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States, 2Institute of Medical Physics and Radiation Protection, Mittelhessen University of Applied Sciences, Giessen, Germany, 3Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States, 4Q Bio Inc, San Carlos, CA, United States
1Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States, 2Institute of Medical Physics and Radiation Protection, Mittelhessen University of Applied Sciences, Giessen, Germany, 3Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States, 4Q Bio Inc, San Carlos, CA, United States
Synopsis
Keywords: Gradients, Brain
Most of EPI ghosting algorithms assume that odd/even of phase modulations, either of first or higher spatial order, are stationary through the readout. Hence, a phase maps (or a linear function) for the subset of odd and even k-space lines is judged enough to model Nyquist ghosting and obtaining ghosting free images. Nevertheless, we demonstrate with field monitoring that for high-gradient strength diffusion MRI, persistent eddy currents from the diffusion module interfere non-linearly with the image encoding, leading to phase modulations that are time-varying during the readout. Implications for existing ghosting correction algorithms and potential alternatives are discussed.Introduction
In this work, we use field monitoring analysis to show that for diffusion MRI utilizing strong gradients on the MGH Connectome scanner, the spatiotemporal profile of phase modulations for odd/even EPI echoes is complex and shows a non-linear time dependence during the readout period, in part due to the interference of slow decaying eddy currents from the strong diffusion-sensitizing gradients [1]. Implications for existing ghosting correction algorithms and potential alternatives are discussed.Methods
Data: All data were acquired on a dedicated high-gradient 3T MRI scanner (MAGNETOM Connectom, Siemens Healthineers) equipped with maximum gradient strength of 300 mT/m. We measured the spatiotemporal evolution of the magnetic field during the readout of the following dMRI EPI sequences.·- 2D single-shot Stejskal-Tanner EPI for b= 2,000 s/mm2 (Gmax = 168 mT/m) and b= 4,000 s/mm2 (Gmax = 238 mT/m), 1 b0-image plus 6 non-collinear directions (see legend of Fig.1), TR/TE = 15,000/90 ms, FOV = 220 x 183 x 100 mm3, in-plane resolution 2 x 2 mm2, slice thickness = 2 mm, no SMS, no acceleration, no PF, EPI factor = 92, echo spacing = 0.53 ms. Total readout = 48.76 ms·
- 3D multi-shot Stejskal-Tanner EPI[2] for b =1,500 s/mm2 (Gmax = 94 mT/m), b= 4,000 s/mm2 (Gmax = 171 mT/m), b = 6,000 s/mm2 Gmax = 232 mT/m), and b = 10,000 s/mm2 (Gmax = 277 mT/m), 1 b0-image plus 6 non-collinear directions, (see legend of Fig.1), TR/TE = 500/81 ms, FOV = 170 x 125 x 176 mm3, no acceleration, no PF, EPI factor =42, #echos = 3, echo spacing = 1.28 ms. Total readout = 50 ms
Analysis: A basis of solid spherical harmonics model up to 3rd order was fitted to the 16 measured phase signals. The spatiotemporal evolution of the phase inside the imaging field of view was expressed as
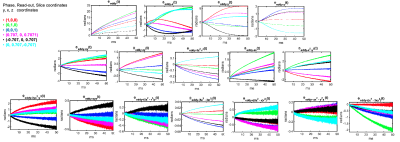
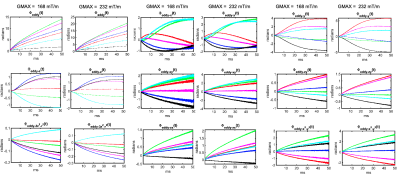
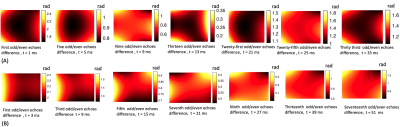
$$\phi(\mathbf{r}, t) = \sum_{l=0}^{15}k_l(t)h_l(\mathbf{r})$$ where $$$h_l(\mathbf{r})$$$ is the l-th spherical basis component and $$$k_l(t) = \int_{0}^{t}G_l(\tau)d{\tau}$$$ is the associated coefficient [4]. To characterize eddy currents from the diffusion module, we subtract the coefficients $$$k_l(t)$$$ of the image encoding trajectory acquired with the six diffusion directions from the $$$k_l(t)$$$ of the trajectory from the b0-image. Assuming the nominal k-space trajectory remains identical and ignoring heating effects, the difference in coefficients $$$k_{eddy-l}(t) = \int_{0}^{t}G_{eddy-l}(\tau)d{\tau}$$$ will capture spatiotemporal variations that depend only on the diffusion gradients (see [4-5]). For each basis, we calculated the maximum accumulated phase (in radians) by $$$\phi_{eddy-l}(t) = k_{eddy-l}(t)h_l(\mathbf{r}_{max})$$$ where $$$\mathbf{r}_{max} = arg max _{r \in FOV} h_l(\mathbf{r})$$$. Plots of $$$\phi_{eddy-l}(t)$$$ generated for 2D and 3D EPI sequences with different diffusion-encoding gradient directions are shown in Figs. 1 and 2, and for different gradients strengths in Figs 3 and 4. Plots of the phase difference between odd and even EPI echoes at different time points during the readout are shown in Fig 5.
Results
Figures 1 and 2 show that eddy currents of up to third order are still active during the majority of the readout. The spatially constant eddy terms (B0 eddy) and those with linear components, particularly along the readout (x), contributed the most to phase errors. Nonetheless, second-order eddy currents appear to contribute significantly, with maximum phase values of up to 4 radians in the middle of the readout. The amplitude of the eddy currents increased as the gradient intensity increased. This is shown in Figs 3 and 4 for both EPI sequences. It is worth noting that some eddy currents, mostly those with a linear component along x, but also those with a bilinear component (xy, xz), exhibited systematic zig-zag behavior with a distance equal to the echo spacing. This phenomenon introduced non-linear high-order changes in the odd/even k-space lines with respect to time over the readout. As a result, phase errors between odd/even lines were modulated in a temporally variable manner, as shown by monitoring the spatiotemporal profile of phase discrepancies between odd/even k-space lines during the readout in Fig 5.Discussion and Conclusions
Eddy currents from strong-diffusion gradients (up to 300 mT/m) interact with the EPI image readout in a non-linear manner, both in space and time. Due to the persistent eddy currents, phase discrepancies between odd/even EPI echoes are of high order and dimension and are modulated differently throughout the readout. As a result, ghosting correction methods that simplify the phase evolution by using only two phase maps corresponding to a subset of odd and even k-space lines may not be ideal for correcting ghosting in high-gradient strength dMRI images. Concurrent field monitoring [6] in conjunction with higher-order image reconstruction [4,7] that incorporates the phase evolution in the forward encoding model may be a better approach to obtaining ghosting-free reconstruction. Such efforts will be important to ensure that ghosting artifacts are minimized as even higher performance gradient systems become available for human imaging [8].Acknowledgements
This work was supported by the NIH grants (P41-EB030006, U01-EB026996, R01-EB021265, K23-NS096056, R01 EB028797, R03 EB031175, U01 EB025162). We would like to thank Christian Mirkes, Cameron Cushing and Paul Weavers from Skope Inc.References
[1] Yi-Cheng Hsu, Ying-Hua Chu, Thomas Witzel, Qiuyun Fan, and Fa-Hsuan Lin, Eddy current characterization and correction using field monitoring for diffusion weighted imaging with maximal strength of 250 mT/m, Proc. Intl. Soc. Mag. Reson. Med. 26 (2018), 5334
[2] Miller KL, Stagg CJ, Douaud G, Jbabdi S, Smith SM, Behrens TEJ, Jenkinson M, Chance SA, Esiri MM, Voets NL, Jenkinson N, Aziz TZ, Turner MR, Johansen-Berg H, McNab JA. Diffusion imaging of whole, post-mortem human brains on a clinical MRI scanner. Neuroimage. 2011 Jul 1;57(1):167-181. doi: 10.1016/j.neuroimage.2011.03.070. Epub 2011 Apr 5. PMID: 21473920; PMCID: PMC3115068.
[3] Barmet C, De Zanche N, Pruessmann KP. Spatiotemporal magnetic field monitoring for MR. Magn Reson Med. 2008 Jul;60(1):187-97. doi: 10.1002/mrm.21603. PMID: 18581361.
[4] Wilm, B.J., Barmet, C., Pavan, M. and Pruessmann, K.P. (2011), Higher order reconstruction for MRI in the presence of spatiotemporal field perturbations. Magn. Reson. Med., 65: 1690-1701.
[5] Valsamis JJ, Dubovan PI, Baron CA. Characterization and correction of time-varying eddy currents for diffusion MRI. Magn Reson Med. 2022 May;87(5):2209-2223. doi: 10.1002/mrm.29124. Epub 2021 Dec 11. PMID: 34894640.
[6] Wilm, Bertram J., et al. "Diffusion MRI with concurrent magnetic field monitoring." Magnetic resonance in medicine 74.4 (2015): 925-933.
[7] Ramos-Llorden G, Park D, Mirkes C, Cushing CM, Weavers P, Lee HH, Tian Q, Scholz A, Keil B, Bilgic B, Yendiki A. Distortion-and ghosting-free high b-value ex vivo human brain diffusion MRI achieved with spatiotemporal magnetic field monitoring, Proc. Intl. Soc. Mag. Reson. Med. 30 (2022), 0232
[8] Huang, Susie Y., et al. "Connectome 2.0: Developing the next-generation ultra-high gradient strength human MRI scanner for bridging studies of the micro-, meso-and macro-connectome." NeuroImage 243 (2021): 118530.
Figures
Coefficients of the spherical component basis that models the eddy current-component part of the phase evolution during a 2D SS EPI image readout with varied diffusion gradient directions. Parameters: single-shot EPI sequence (no SMS) on the 3T Connectom scanner with b = 4,000 s/mm2 and Gmax = 238 mT/m. A middle-axial slice (z = 20 mm) was chosen. It is worth noting that the accumulated eddy current phase for the majority of cases does not reach a constant value during the readout, indicating that the magnetic fields generated by eddy currents are still present in the majority of the readout.
Coefficients of the spherical component basis that models the eddy current-component part of the phase evolution during a 3D multi-shot EPI image readout when different diffusion gradient directions are played out. (see Legend for orientation) Parameters: 3D multi-shot EPI sequence (with b = 10,000 s/mm2) at Gmax = 277 mT/m on the 3T Connectom scanner. Trajectories are shown for a kz plane close to the center (kz = 34 rad/m from a maximum of 3000 rad/m) and for the first of the three shots (similar behavior was found for 2nd and 3rd shots).
Eddy current behavior with respect to diffusion gradient strength for a 2D single-shot EPI sequence (same parameters as in Fig.1). The amplitude of eddy currents increases with gradient strength as expected for the majority of the spherical basis components, whereas the temporal behavior remains quite comparable. Only components up to the second order are displayed.
Eddy current behavior with respect to diffusion gradient strength for a 3D multi-shot EPI sequence (same parameters as Fig.2). Only the first shot is displayed. The amplitude of eddy currents increases with gradient amplitude, as expected for most of the spherical basis components, while the temporal evolution remains quite similar. Only components up to the second order are displayed.
Temporal evolution of the phase modulation (odd-even EPI echo differences maps) sampled at different time points of the readout for A) 2D single-shot EPI with b =4 000 s/mm2, Gmax = 232 mT/m, B) 3D-multi-shot EPI with b = 10,000 s/mm2 , (Gmax = 277 mT/m), first shot. The rest of the parameters are the same as described in the caption of Fig 1 and 2, respectively. Note the high-order spatial variations, with prominent variation along the readout axes (x). The temporal evolution of the spatial distribution is non-linear in time. Substantial changes can be seen at the beginning of the readout.
DOI: https://doi.org/10.58530/2023/4421