Synopsis

Keywords: Shims, Shims, multi-coil

Multi-Coil shimming is advantageous because of its ease of use for effective local and slice-wise shimming. Shim coils are constructed of current-carrying conductor wires and undergo Lorenz force while placed in the magnet. Currents alteration in slice-wise shimming changes the magnitude and direction of force and imposes mechanical vibrations and acoustic noise. Here we propose strategies to control the level of inter-slice shims current change. The proposed strategies showed that inter-slice shims current change can be appropriately reduced by applying a minor change into shimming routine and without degrading shimming performance significantly .

Introduction

Inhomogeneity of static magnetic field, B0, increases at ultrahigh-field (UHF) MRI because of induced magnetic fields from susceptibility differences which is a linear function of B0 strength. In the human brain, inhomogeneity spots are local and steep, formed around air-tissues interfaces. Shimming using a Multi-Coil (MC) setup^1,2 is advantageous for human brain shimming at UHF because of its architecture where employing small local coils allows increasing number of shim coils and targeting local inhomogeneities.

B0 shimming problem is usually an overdetermined system of linear equations; hence, shimming of a reduced ROI is expected to yield an improved homogeneity³. In a reduced ROI, the target field can be better approximated with a fixed number of shim coils. Slice-wise shimming takes advantage of this notion by calculating optimal shims current per slice in advance and performing dynamic shim update (DSU) during acquisition.

A current-carrying conductor in presence of a magnetic field experiences a so-called Lorenz force. At UHF where the field strength is higher and the desire is toward increasing shims current and/or utilizing coils with more turns, local shim coils undergo higher Lorenz force. DSU alters Lorenz force magnitude and/or direction and results in mechanical vibration and acoustic noise which can degrade data quality if not addressed properly, damage the setup in long-term, or discomfort subject since the setup is physically attached to RF head coil. In this work, we propose some tactics to tackle and reduce Lorenz force temporal fluctuations during an experiment with DSU.

Methods

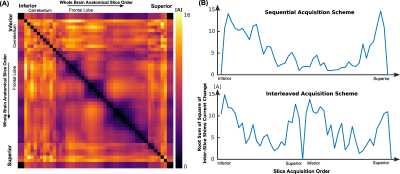
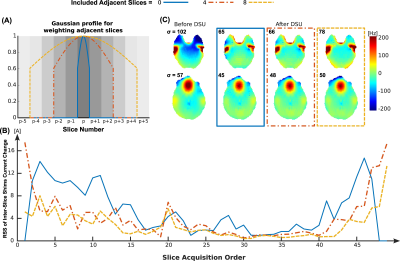
Simulation results in figure 1.A depicts the root sum of square (RSS) of shims current change ($$$\sqrt{\sum_{i=1}^{16} (c_{i(k)}-c_{i(m)})^{2}}$$$) when moving from slice k to slice m for shimming of a target brain B0 map with a 16-channel multi-coil setup⁴ (current limit = ±3A). Figure 1.B represents RSS of shims current change for two conventional acquisition schemes, sequential and interleaved. Although B0 inhomogeneity varies smoothly in adjacent slices; however, figure 1 shows that it is not guaranteed that minor shims current change is sufficient to reach the most optimum solution. Here we propose the following approaches to control Lorenz force alterations in DSU:

1) Covering both adjacent slices for slice-wise shimming is used to avoid shim degeneracy and improve orthogonality for shims basis-set⁵. This can be expanded to more than two adjacent slices. With more adjacent slices involved, more similarity in shims setting is expected for consecutive slices at the cost of lowering shimming efficiency. To recover efficiency loss, a Gaussian profile is applied to control the contribution of each slice (Figure 2.A). Thus, shimming optimization can be formulated as:
$$\tilde{c} = \underset{c}{arg min} \parallel Ac+\Delta B_{0} \parallel_{w}^{2} \qquad s.t. \quad lb\leq c\leq ub \qquad(1)$$
where c is currents to be calculated, A is shims basis set, and W is NxN (N=number of voxels) diagonal matrix containing weights from a Gaussian profile.

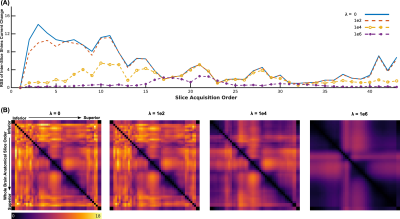
2) Schwerter et al.⁶ proposed to add two additional regularization terms and dynamic constraints to dampen eddy-current in DSU. Here we employ a simplified form of that algorithm with one regularization to regulate inter-slice shims current change. Hence, the shimming problem can be reformulated as:
$$\tilde{c} = \underset{c}{arg min} \parallel Ac+\Delta B_{0} \parallel_{2}^{2}+\lambda\parallel c-\dot{c} \parallel_{2}^{2} \qquad s.t. \quad lb\leq c\leq ub \qquad(2)$$
where λ is regularization weighting parameter and ċ is the calculated shims current for preceding slice.

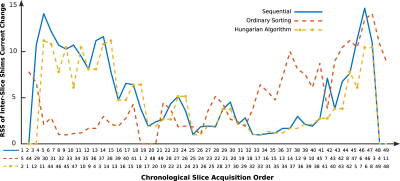
3) Shims current is calculated per slice first. Then, slice acquisition order will be sorted in a way that overall inter-slice currents change reduces. A simple sort method is to pick a slice as starting and calculate RSS of shims current change with respect to every other slice and choose the one that gives the minimum value. This can be simply repeated for all slices in a loop. From optimization perspective, this is a form of linear assignment problem and can be effectively solved with methods like Hungarian algorithm.

Results and Discussions

Figure 2.B shows RSS of inter-slice currents change for sequential acquisition with different number of adjacent slices involved in shimming. Integral of RSS plot (iRSS) can be used as a metric to compare inter-slice current change reduction. iRRS is 257, 203, and 136 for the case of including 0, 4, and 8 adjacent slices in shimming of a target slice, respectively. Figure 2.C depicts B0 maps before and after DSU, including different number of adjacent slices.

RSS with different regularization weights to dampen inter-slice currents change is shown in figure 3.A. As expected, iRSS reduces with larger regularization weights; however, whole brain STD has not affected much (iRSS=257, 230, 111, and 34 and SD=35.89, 35.89, 35.93, 37.81 Hz for λ=0, 1e2, 1e4, and 1e6, respectively. SD before DSU=74 Hz). Figure 3.B shows that a larger regularization weight can dampen RSS for any acquisition order, not just sequential or interleaved schemes.

Figure 4, compares RSS for sequential scheme, ordinary, and Hungarian acquisition order sorting (iRSS=257, 236, and 215 for sequential, ordinary, and Hungarian, respectively). RSS increases moving to the end of acquisition for ordinary sorting since fewer slices are left to be chosen for minimum RSS. Unlike the two other approaches, ordinary and Hungarian sorting methods do not affect shimming efficiency as they only change chronological acquisition order.

Acknowledgements

No acknowledgement found.