4413
Optimisation of pulse-specific phase schedule reduces peak RF amplitude in multiband parallel-transmit pulses
Belinda Ding1,2, Sydney Nicole Williams1, Minghao Zhang3, Jürgen Herrler4, Patrick Liebig4, Iulius Dragonu5, Radhouene Neji5, Christopher T. Rodgers3, and David A Porter1
1Imaging Centre of Excellence, University of Glasgow, Glasgow, Scotland, 2Siemens Healthcare Ltd., Glasgow, United Kingdom, 3Wolfson Brain Imaging Centre, University of Cambridge, Cambridge, United Kingdom, 4Siemens Healthcare GmbH, Erlangen, Germany, 5Siemens Healthcare Ltd., London, United Kingdom
1Imaging Centre of Excellence, University of Glasgow, Glasgow, Scotland, 2Siemens Healthcare Ltd., Glasgow, United Kingdom, 3Wolfson Brain Imaging Centre, University of Cambridge, Cambridge, United Kingdom, 4Siemens Healthcare GmbH, Erlangen, Germany, 5Siemens Healthcare Ltd., London, United Kingdom
Synopsis
Keywords: Parallel Transmit & Multiband, Parallel Transmit & Multiband, phase schedule
Multiband(MB) imaging can greatly reduce scan time, but MB pulses often encounter peak amplitude constraints. An optimal phase schedule has been published for traditional single-transmit (sTx) RF pulses. However, after an initial evaluation, we found that it only has marginal benefits for parallel-transmit (pTx) pulses. We compared four common optimisation algorithms (fmincon, fminsearch, simmulated annealing, global search) to determine the most suitable algorithm for choosing the best offset phases for a pTx pulse. Overall, fmincon efficiently selected the optimal phase schedule of a pTx pulse and lowered peak amplitude by an average of 15% when MB-factor=3.Introduction
Simultaneous multislice(SMS) or multiband(MB) imaging allows several slices to be imaged simultaneously and dramatically reduces scan time. The simplest way to obtain MB excitation is to sum multiple RF pulses with different frequency modulations:$$RF_{MB}(t)=RF_{SB}(t)\sum_{k=1}^{N} e^{i(γGtx_k+\phi_k)}$$
where $$$RF_{MB}(t)$$$=MB-RF waveform, $$$RF_{SB}(t)$$$=single-band waveform, N=MB-factor, G=slice-select gradient amplide, and $$$x_k$$$ and are the spatial location and phase offset for kth slice.
If $$$\phi_k$$$ is identical for all slices and slices are in phase at t=0, the MB pulse’s peak amplitude scales with N. As such, MB-pulses are prone to exceed the scanner peak amplitude limit. Peak amplitudes can be reduced by allowing the phase of each slice to vary, and an optimal phase schedule published by Wong is widely used for this[1].
Parallel RF transmission (pTx) plays a vital role in reducing B1+ inhomogeneity associated with ultra-high-field (UHF, B0 ≥ 7 T) imaging. In pTx, the complex-valued relationship between transmit channels varies spatially with static pTx or B1+ shimming, offering additional degrees of freedom to homogenise B1+[2].
With these additional degrees of freedom, the solution space of optimal phases to reduce peak RF amplitude increases beyond those provided by Wong[1]. This is because the phase difference between pTx channels often varies along the slice dimension producing summation patterns for SMS that might be ill-suited compared to the case of single transmission (sTx) with uniform summation across channels (Figure 1).
This abstract aims to evaluate the effectiveness of using the optimal single-transmit (sTx) phase schedule in pTx pulses and compares different algorithms in choosing the best offset phases for a pTx pulse. Initially, slice-selective B1+ shimming is investigated.
Methods
Both sTx and pTx MB-RF were created by summing single-band sinc pulses using the CP and slice-specific B1-shimmed complex coefficients (pTx), with no phase offset and the sTx optimal phase schedule[1]:$$RF_{MB,j}(t)=RF_{SB}(t)\sum_{k=1}^{N}w_{i,j}e^{i(γGtx_k+\phi_k)}, j =1,2,...8$$
where the RF shim vector w has a unit norm and $$$w_{i, j}=\frac{1}{\sqrt{8}}e^{i(2\pi/8)(j-1)}$$$ in CP mode for an 8Tx system.
Using a factorial study design, MB-pulses were created with these parameters: 2 shim coefficients types (CP/pTx) x 5 pulse durations (2,4,6,8,10ms) x 5 time-bandwidth products (2,3,4,5,6) x with/without Hanning filter x 5 different MB factors (2,3,4,5,6) x no phase offset/sTx optimal phase schedule[1]. For pTx pulses, slice-specific shim coefficients were calculated from per-channel B1+ maps obtained from 6 healthy volunteers (saturation-recovery turbo-FLASH, 34 axial slices, 3mm slice (30% gap)).
Optimal multiband offset phases were calculated for one Hanning-filtered sinc pulse (duration=4ms, TBW=4) using four optimisation methods (fmincon, fminsearch, simulated annealing, global search) for MB-factors=3,4,5,6 in all volunteers. All optimisations were performed in MATLAB (R2022a). Optimal sTx phases were used as starting points, and the solutions were bounded between 0 and 2 when applicable. Paired Student’s t-tests were conducted between optimisation methods, and the Holm-Bonferroni method was used to correct for multiple comparisons [3]. An exhaustive grid search was also performed for MB-factor=3. Each optimisation method was repeated 50 times with random starting values in one MB pulse to assess each method’s stability.
The feasibility of a universal solution was also investigated by comparing the similarity between slice-specific shim vectors and optimal phases between volunteers.
Results and Discussion
Peak B1+ across all channels evaluating the optimal sTx phases in pTx MB pulses are presented in Figure 2. Overall, using optimal sTx phases results in lower peak B1+ than using no phase offsets. However, the reductions are slight compared to sTx pulses.Figure 3 compares the solutions from each optimisation method against the minimum peak amplitude obtained through the grid search method in an MB3 pulse. Figures 4A-C present results from higher MB-factors.
All four optimisation methods provided drastic reductions in peak B1+ (15%-40%), and although the differences between the methods are statistically significant, the actual differences are very small and unlikely to have any practical impact to SAR management and RF pulse design.
Global optimisation methods (simulated annealing, global search) outperformed non-linear optimisation methods (fmincon, fminsearch) but their long optimisation times make them unfeasible for inline pulse design (Figure 4B). Overall, fmincon was better and more reliable than fminsearch, which is likely because fmincon uses a gradient-based approach. However, the optimisation time of fmincon increases drastically with the MB factor. Thus, simulated annealing may be more reliable and equally time-efficient for high MB factors.
For slice-by-slice static pTx, the database of 6 subjects showed low degrees of similarity amongst cross-subject shims, discouraging the pursuit of universal slice-specific shims (Figure 5a). The optimised phases also varied greatly between subjects and shims (Figure 5b).
Future work will require decreasing computation time to implement this subject-specific phase optimisation approach for pTx SMS in practice (e.g. by including gradient information in the optimiser). This is particularly true for higher MB factors or with an extension of this study to dynamic pTx (e.g., slice-selective spokes). Additionally, this work could be explored at the point of MB pulse design, where introducing a looser peak RF amplitude constraint before phase optimisation could improve pTx performance.
Conclusion
Overall, we have shown that using sTx optimal phase schedule has only marginal benefits when applied to a pTx MB pulse and shim-specific phase optimisation should be performed to reduce peak RF amplitude.Acknowledgements
MZ is supported by the Medical Research Council (grant number MR N013433-1) and the Cambridge Trust.References
[1] Wong, E. Optimized Phase Schedules for Minimising Peak RF Power in Simultaneous Multi-Slice RF Excitation Pulses. in Proc. 20th Annu. Meet. ISMRM vol. 20 (2012).
[2] Padormo, F., Beqiri, A., Hajnal, J. V. & Malik, S. J. Parallel transmission for ultrahigh-field imaging. NMR Biomed. 29, 1145–1161 (2016).
[3] Holm, S. A Simple Sequentially Rejective Multiple Test Procedure. Scandinavian Journal of Statistics 6, 65–70 (1979).
Figures
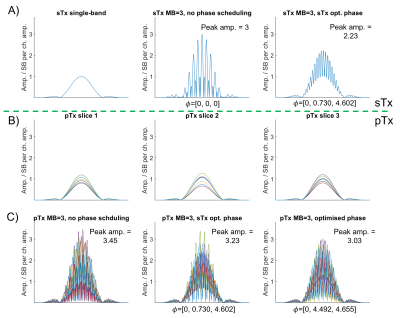
Example of the complexity of phase
scheduling for MB-pTx. A)
Phase scheduling for MB3 single-transmit (sTx)
pulse. A sinc
waveform (left) triples in amplitude (centre) without phase scheduling, but
only increases 2.2-fold with phases from Wong(right). B) For MB pTx
pulse, all three slices have unique amplitude (and phase, not shown)
configurations. C) In this example, the amplitude decreases slightly with the sTx
phases (centre) but a more optimal solution exists (right).
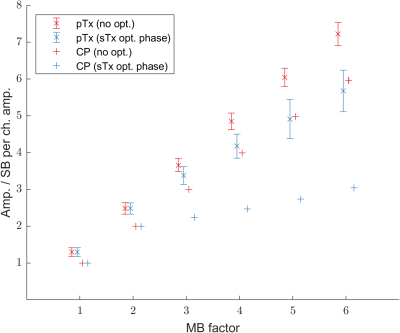
Maximum peak B1+ in CP and
B1-shimmed RF pulses comparing no phase offsets and the optimal sTx
phase schedule from Wong (2012).
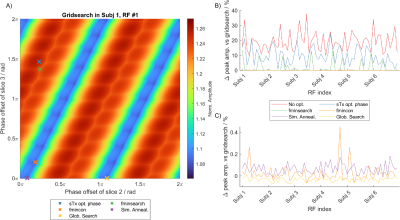
A) Exhaustive grid search shown for
one subject and one MB3 RF pulse with crosses showing the optimal phases found
by each algorithm. B) Percentage changes in peak amplitudes from each algorithm
and the minimum solution found by the grid search in an MB3 pulse across all
subjects. A zoomed-in version of the figure showing solutions from three of the
optimisation method is presented in C.
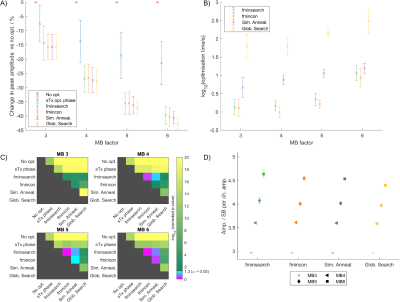
A) Mean±SD
(standard deviation) percentage changes in peak amplitudes between no
optimisation and different phase schedules for MB=3-6. B) Mean±SD
optimisation times across volunteers plotted on a logarithm scale. C) Corrected
p-values between optimisation methods plotted on a negative-logarithm scale.
p>0.05 pairs have different colours. D) Mean±SD peak
amplitudes from 50 runs with random starting values in one subject.
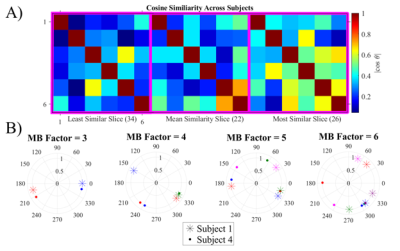
Investigation of subject-dependence of
optimal phase schedules with pTx. A) Magnitude cosine similarity
matrices of slice-specific shims across subjects in 3 slices (1 means an
exact match). Similarity is low in all slices (most similar has mean value of
0.53). B) Polar plot comparison of optimal phase schedules for the two least
similar (w.r.t cosine similarity) subjects, 1 and 4. All MB factor phase shims
are from the global search optimisation and the first slice pair of MB pulses.
Each colour represents the phase offset for a new slice (first slice phase=0,
not shown).
DOI: https://doi.org/10.58530/2023/4413