Synopsis

Keywords: RF Pulse Design & Fields, High-Field MRI

The Universal Pulse (UP) concept to parallel transmission radiofrequency (RF) pulse design was introduced to avoid time consuming B₁⁺ and ΔB₀ data acquisition before each clinical scan. Introduced large flip angle design methods utilize kT-point trajectories and small tip angle approximation. In this work, new quasi damping scheme for Newton's methods method is introduced for large flip angle universal pulse design using numerical solution of the Bloch equation. Introduced quasi-damping scheme can be utilized in large flip angle Universal Pulse design for all flip angles including 180^o pulses, without the loss of performance.

Introduction

The Universal Pulse (UP) concept to parallel transmission radiofrequency (RF) pulse design was introduced by Gras¹ in order to avoid time consuming and data acquisition before each clinical scan. Previously, large flip angle ( ) universal pulses have been introduced, however these methods combine kT-point trajectories with the small tip angle (STA) framework^2-4. In contrast, large flip angle pulses are typically designed using the numerical solution of the Bloch equation via Euler-Rodrigues rotation formula^5,6. In this work, solving the Bloch equations directly is combined with the Newton’s method with a novel quasi-damping scheme for the design of high performance large flip angle UPs.

Methods

Numerical solution of the Bloch equation via Euler-Rodrigues rotation formula⁶ is used herein for designing large flip angle universal parallel transmission pulses for a given gradient trajectory instead of the small tip angle approximation⁷. All relaxation effects are ignored for the pulses designed in this work. The calculated magnetization for all 18 volunteers is denoted as $$$M$$$ and the desired magnetization as $$$M_{des}$$$. Initially, the magnetization $$$M$$$ is assumed to be in z- direction. The desired magnetization for excitation pulses is $$$M_{des}=\left[\begin{matrix}0&sin(\alpha_{des})&cos(\alpha_{des}) \end{matrix}\right]^T$$$ for a rotation around the x-axis with angle $$$\alpha_{des}$$$. For the design of UPs the cost function $$$||M-M_{des}||_2^2$$$ was minimized using the Newton’s method. Defining pulses in vector form as $$$p$$$ and pulse value updates at each iteration as $$$\Delta p$$$, the pulse update can be calculated as $$$\Delta p_k=J^{-1}(M_{des}-M)$$$ for iteration $$$k$$$. $$$J$$$ indicates the Jacobian matrix, which is calculated by the finite difference method, and $$$M_k$$$ denotes the solution of Bloch equation using $$$p_k$$$ . Then, the pulse for the next iteration is calculated as $$$p_{k+1}=p_k+\Delta p_k$$$. Due to ill-conditioning of $$$J$$$ , Moore-Penrose pseudo inverse with tolerance $$$10^{-3}$$$ is used for calculating $$$\Delta p$$$ at each iteration.
Instead of classical damping where pulse updates are scaled with the step size $$$\gamma<1$$$, such that $$$p_{k+1}=p_k+\gamma\Delta p_k$$$ , damping herein is realized by increasing $$$\alpha_{des}$$$ step wise as iterations progress. This method will be denoted as quasi-damping with $$$N$$$ steps, where $$$N$$$ denotes the total number of increment steps for $$$\alpha_{des}$$$. $$$N=1$$$ indicates that no damping is used. In order to design $$$180^o$$$ pulses at least 2 steps for $$$\alpha_{des}$$$ are required since $$$J$$$ has all zero rows for magnetization in z direction and $$$M_{des}$$$ has all zero elements for magnetization in x and y direction. This also prevents the use of classic damped Newton’s method for pulse design regardless of the $$$\gamma$$$ .
An existing dataset with single channel $$$B_1^+$$$ and $$$\Delta B_0$$$ maps for 18 volunteers presented in Geldschlaegber et al⁸ is utilized for universal large flip angle pulse design while testing the introduced quasi-damping scheme. In this work, 2D excitation UPs are designed with a fixed gradient trajectory shown in Figure 1. UPs designed using 1-5 steps with 3 iterations at each step for $$$90^o$$$ pulse and 2-6 steps with 3 iterations at each step for $$$180^o$$$ pulse are compared against UPs designed with the classically damped Newton method and STA UPs. Normalized root mean squared error (NRMSE) calculated from the desired versus the magnetizations generated by UPs is used as the measure of pulse performance.

Results

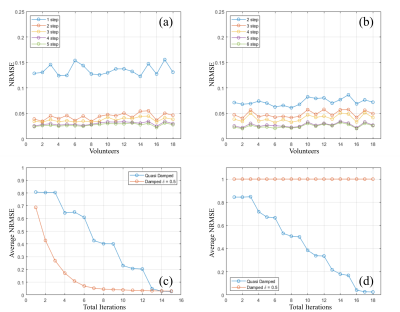
Figures 2 and 3 show that $$$90^o$$$ and $$$180^o$$$ UPs designed via the proposed Newton method with quasi-damping result in highly uniform excitation profiles for all 18 subjects, which is not the case for STA based UPs. NRMSE plots shown in Figure 4(a,b), indicate that the proposed quasi-damping scheme for Newton’s method increases the performance of UPs as the number of steps increase. UPs based on the non-damped Newton’s method $$$(N=1)$$$ have substantially higher NRMSEs than any pulse design using the quasi-damped Newton method (Figure 4(a)). However, the decrease in NRMSE gets smaller as the number of steps increase. Similarly, $$$180^o$$$ pulses with 5 and 6 steps perform clearly better than pulses designed using a lower number of steps, indicating that performance of UPs can be increased via quasi-damping independently of the desired flip angle. Figure 4(c) shows that the proposed quasi-damping method results in the same average NRMSE as the damped Newton’s method, with step size $$$\gamma = 0.5$$$ , in 15 total iterations for the $$$90^o$$$ pulses. On the other hand, Figure 4(d) shows that the damped Newton’s method cannot be used for $$$180^o$$$ pulses whereas the quasi-damped Newton’s method works well for $$$180^o$$$ UP design.

Discussion and Conclusion

In conclusion, the newly introduced quasi-damping scheme can be utilized in large flip angle Universal Pulse design for all flip angles including $$$180^o$$$ pulses, without the loss of performance.

Acknowledgements

This work was funded by Cancer Prevention and Research Institute of Texas (CPRIT) RR180056 and was performed under the rubric of the Advanced Imaging Research Center, UT Southwestern Medical Center.