4407
Efficient Use of Specific Absorption Rate Limits Through Sub-Population Universal Pulses in Parallel Transmission
Igor Tyshchenko1, Simon Lévy2, Jin Jin3, Bahman Tahayori4, and Leigh A. Johnston1
1Department of Biomedical Engineering, The University of Melbourne, Melbourne, Australia, 2MR Research Collaborations, Siemens Healthcare Pty Ltd, Melbourne, Australia, 3MR Research Collaborations, Siemens Healthcare Pty Ltd, Brisbane, Australia, 4The Florey Institute of Neuroscience and Mental Health, Melbourne, Australia
1Department of Biomedical Engineering, The University of Melbourne, Melbourne, Australia, 2MR Research Collaborations, Siemens Healthcare Pty Ltd, Melbourne, Australia, 3MR Research Collaborations, Siemens Healthcare Pty Ltd, Brisbane, Australia, 4The Florey Institute of Neuroscience and Mental Health, Melbourne, Australia
Synopsis
Keywords: Parallel Transmit & Multiband, Parallel Transmit & Multiband, Universal pulses, safety margins, 7T MRI
Universal pulse (UP) design in parallel transmit (pTx) imaging is a calibration-free technique that can effectively mitigate the radiofrequency (RF) field inhomogeneity over a population in ultra-high field MRI. In this work, we explore a middle-ground approach of using sub-population UPs. Assuming the entire population is divided into sub-populations by grouping similar anatomical shapes and positions, UPs can thus be designed with reduced intersubject variability. In this preliminary study of head imaging, it is demonstrated that sub-populations of various sizes centred at the mean shape and position can reduce safety margins and improve UP’s performance.Purpose
Parallel transmit (pTx) universal pulse (UP) design is a calibration-free technique that can effectively mitigate the radiofrequency (RF) field inhomogeneity over a population1. As UPs cover a large population distribution, they lead to inferior performance compared to solutions tailored to each subject. In this work, we hypothesised that by reducing the anatomic variability through sub-populations, a less restrictive safety margin could be applied during the pulse design, allowing more efficient use of specific absorption rate (SAR) limits.Methods
The three most SAR-sensitive head model parameters2 were selected: head breadth (HB), head length (HL) and Y-shift (Fig. 1, left). The population distribution was defined by modelling parameters as Gaussian random variables with means $$$\mu_{i}$$$ and standard deviations $$$\sigma_{i}$$$ of a Caucasian population3.Sub-populations were constructed by reducing $$$\sigma_{HB}$$$, $$$\sigma_{HL}$$$ and $$$\sigma_{Y}$$$ to 50% and 25% of their original values. 21 representative anatomies were generated for each sub-population following the multivariate (Fig. 1, right) and univariate unscented transform sampling scheme4. Anatomies were loaded in a generic 8-ch pTx coil for numerical modelling (Sim4Life by ZMT, Zürich, Switzerland), tuned and matched for the Duke V3.0 (IT’IS, Zurich, Switzerland). $$$B_{1}^{+}$$$-maps and Q-matrices were derived from Finite-Difference Time-Domain (FDTD) simulation with 1.5×1.5×1.5 mm3 isotropic resolution for all anatomies. For each sub-population, a 5kT-UP inversion pulse was computed using the active-set MATLAB algorithm (Mathworks, Natick, MA)5,6, based on the $$$B_{1}^{+}$$$-maps after being resampled to 5×5×5 mm3 isotropic resolution. Specifically, a magnitude least squares optimisation problem with the target normalised longitudinal magnetisation profile $$$M_{z}=-1$$$ was solved subject to strict power and SAR constraints. All three sub-populations were centred at the mean head shape with zero Y-shift. They were optimised using the same virtual observation points (VOP) model that was derived for the centre anatomy7.
The SAR distribution was studied by fitting a second-order multivariate polynomial to the SAR values of the 21 representative anatomies2. An additional six test anatomies unseen by the pulse design algorithm were selected at $$$\pm \sigma_{i}$$$ for each parameter, to validate the fit. Extreme value theory (EVT) was applied to model large SAR deviations found in the tail of the distribution8. For each sub-population, a safety margin was derived, for which the probability of exceeding (underestimating) the SAR was no larger than 1% for each set of 175 scans (a model of 25 scans per day within any given week). These sub-population-specific intersubject variability safety margins combined with the two additional margins, 1.25 and 1.55, accounting for modelling errors9 and measurement uncertainties10, respectively, were considered in the pulse design.
Results
Three 10g peak SAR distributions (Fig. 2) illustrate how the SAR variance reduces for decreased intersubject variability. As a result, a smaller anatomical safety margin can be applied. Narrower populations without any margins introduced resulted in a noticeable NRMSE improvement (Fig. 3). The one-size-fits-all solution performance can be improved by up to 10% when the standard deviation is 25% of the original value. Because no safety margins were applied, the improvement can be explained by the smaller volume of interest in describing representative anatomies. As the standard deviation decreases, the anatomies appear closer to the average case. This explains the considerable difference between the NRMSE performance of the 100% distribution and its counterparts with smaller anatomical variabilities (Fig. 3, dash vs solid lines).Figure 4 illustrates the performance metrics when all three safety margins are applied. It is observed that the performance deteriorated compared to the unrestricted case in Figure 3. The average performance gains increased, reaching a 16% improvement in the 25% sub-population. The overall comparison of different sub-populations is summarised in figure 5.
Discussion & Conclusion
This study demonstrates that anatomical sub-populations have the potential to improve head imaging at 7T. Our proof-of-concept results indicate that pTx pulse design based on sub-populations of anatomies can reduce SAR variability and enhance performance. It is important to note, however, that different UPs would be required for each individual sub-population, increasing the complexity of pulse design and safety monitoring.Significant NRMSE improvements can be attained for relatively narrow parameter distributions of around 25%. Further reduction would render computation time unreasonably high. For example, with three parameters in the model and assuming we want to split the population distribution into three groups along each parameter, the total number of pulses required is 27. As a compromise, in addition to a population with full coverage of three parameters, it will be beneficial to have a sub-population with partial parameter coverage around the mean. This sub-population will be able to cover a significant proportion of anatomies and still provide improved pulse performance.
Similar to the design of the UP for sub-populations in the current study, in principle, the VOPs can be designed for the sub-populations as well. It is anticipated that sub-population VOPs will enable more accurate SAR estimation and less restrictive safety constraints compared to the VOPs generated for the whole population.
Acknowledgements
The authors wish to acknowledge ZMT Zurich MedTech for providing the simulation software package Sim4Life.References
- Gras V, Vignaud A, Amadon A, Le Bihan D, et al. Universal pulses: a new concept for calibration‐free parallel transmission. Magnetic resonance in medicine. 2017;77(2):635-43.
- Le Garrec M, Gras V, Hang MF, et al. Probabilistic analysis of the specific absorption rate intersubject variability safety factor in parallel transmission MRI. MRM. 2017;78(3):1217-23.
- Ball R, Shu C, Xi P, et al. A comparison between Chinese and Caucasian head shapes. AE. 2010;41(6):832-9.
- Shao Y, Zeng P, Wang S. Statistical simulation of SAR variability with geometric and tissue property changes by using the unscented transform. MRM. 2015;73(6):2357-62.
- Hoyos-Idrobo A, Weiss P, Massire A, et al. On variant strategies to solve the magnitude least squares optimization problem in parallel transmission pulse design and under strict SAR and power constraints. IEEE T-MI. 2013;33(3):739-48.
- Gras V, Luong M, Amadon A, et al. Joint design of kT-points trajectories and RF pulses under explicit SAR and power constraints in the large flip angle regime. JMR. 2015;261:181-9.
- Orzada S, Fiedler TM, Quick HH, Ladd ME. Local SAR compression algorithm with improved compression, speed, and flexibility. Magnetic resonance in medicine. 2021;86(1):561-8.
- De Haan L, Ferreira A. Extreme value theory: an introduction. Springer Science & Business Media; 2006.
- Ferrand G, Luong M, Amadon A, et al. Mathematical tools to define SAR margins for phased array coil in-vivo applications given E-field uncertainties. In Proceedings of the International Society of Magnetic Resonance in Medicine. 2015.
- Gumbrecht, R. Development of customized pTx MR excitation methods and their safe application. Doctoral Thesis. FAU. 2013.
Figures
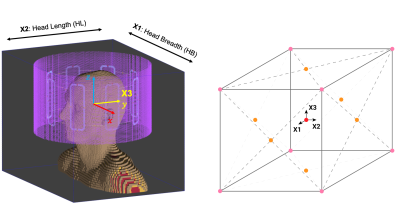
Figure 1. Left: 8-ch pTx coil and average head model with three parameters: head breadth (HB), head length (HL) and Y-shift. Right: Unscented transform multivariate sampling scheme diagram for three variables: 8 corner (pink) cases $$$(\pm \sigma_{HB}, \pm \sigma_{HL}, \pm \sigma_{Y})\sqrt{5/3}$$$; 6 edge (orange) cases $$$(0,\pm \sigma_{i},0)\sqrt{5}$$$ and a centre (red) case $$$(0,0,0)$$$.
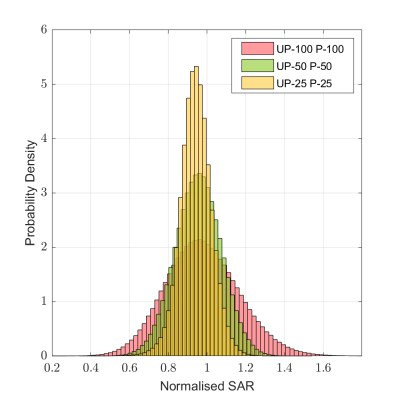
Figure 2. Peak 10g SAR distributions for different 5kT-UP pulses within their respective populations. The SAR values are normalised by the average model with the mean head shape and zero Y-shift. “UP-N P-N” represents a 5kT-UP pulse designed based on an N% sub-population and evaluated by drawing at random 106 samples from the same N% sub-population.
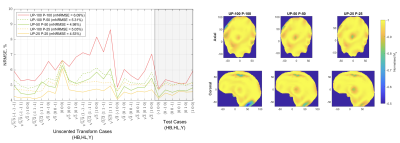
Figure 3. Left: Pulse performance as measured by the normalised root mean square error (NRMSE) on the target magnetisation profile. The mean NRMSE (mNRMSE) across all 27 cases is given in brackets. “UP-N P-M” represents a UP designed for an N% sub-population evaluated on samples from an M% sub-population. No safety margins were applied during the pulse design. Right: Axial and coronal normalised longitudinal magnetisation profiles for the largest anatomy in each population, $$$(+ \sigma_{HB}, + \sigma_{HL}, + \sigma_{Y})\sqrt{5/3}$$$.
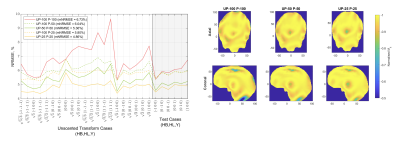
Figure 4. Left: Pulse performance as measured by NRMSE and mean NRMSE across all 27 anatomies. “UP-N P-M” represents a UP designed for a N% sub-population evaluated on samples from an M% sub-population. Horizontal axis are normalised sigma points (HB, HL, Y-shift). Different anatomical safety margins were applied during the pulse design: 1.72 (P-100), 1.37 (P-50) and 1.25 (P-25). Right: Axial and coronal normalised longitudinal magnetisation profiles for the largest anatomy in each population, $$$(+ \sigma_{HB}, + \sigma_{HL}, + \sigma_{Y})\sqrt{5/3}$$$.
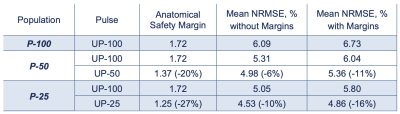
Figure 5. Summary of safety margins and performance metrics of different 5kT-UP.
DOI: https://doi.org/10.58530/2023/4407