4361
Deep learning-based groupwise registration for longitudinal MRI analysis in glioma1Department of Radiology & Nuclear Medicine, Erasmus MC, Rotterdam, Netherlands, 2Department of Imaging Physics, Delft University of Technology, Delft, Netherlands, 3Medical Delta, Delft, Netherlands, 4Department of Pathology, Amsterdam UMC / VU Medical Center, Amsterdam, Netherlands, 5Laboratory for Childhood Cancer Pathology, Princess Máxima Center for Pediatric Oncology, Utrecht, Netherlands, 6Department of Neurosurgery, Amsterdam UMC / VU Medical Center, Amsterdam, Netherlands, 7Department of Neurology, Erasmus MC Cancer Institute, Rotterdam, Netherlands, 8Department of Neurology, Amsterdam UMC / VU Medical Center, Amsterdam, Netherlands, 9The Jackson Laboratory for Genomic Medicine, Farmington, CT, United States, 10Department of Neurosurgery, Amsterdam UMC/VUmc, Amsterdam, Netherlands
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Data Analysis, Image Registration
Glioma growth may be quantified with longitudinal image registration. However, the large mass-effects and tissue changes across images suposse an added challenge. Here, we propose a longitudinal, learning-based and groupwise registration method for the accurate and unbiased registration of glioma MRI. We evaluate on a dataset from the Glioma Longitudinal AnalySiS consortium and compare to classical registration methods. We achieve comparable Dice coeffients, with more detailed registrations, while significantly reducing the runtime to under a minute. The proposed methods may serve as an alternative to classical toolboxes, to provide further insight into glioma growth .Introduction
Glioma progression is monitored by routine MR scanning, enabling that tumor growth can be evaluated with respect to earlier time-points. This growth may present both as a mass effect and as an extension of abnormalities into previously healthy tissue. To accurately assess tumor growth and tumor-induced deformations, longitudinal intrasubject image registration is often used. However, such registration in cases with large deformations and tissue change is highly challenging.Longitudinal image registration may benefit from groupwise strategies in which multiple images are concurrently aligned. This avoids introducing bias towards an a priori selected reference image [1]. However, existing learning-based methods for image registration mostly concern pair-wise approaches [2]. Moreover, the few proposed learning-based methods for groupwise registration are designed for analysis of images without pathologies, and are prone to fail registering glioma images. To bridge this gap, we present a learning-based method for non-linear registration of longitudinal glioma images.
Methods
We used T2-weighted FLAIR MRI scans of 61 participants from the multi-center GLASS-NL study [3]. Participants were initially diagnosed with lower-grade (grade 2 or 3) IDH-mutant astrocytoma and underwent multiple surgical resections. Images were affinely aligned to the ICBM 2009a nonlinear asymmetric atlas [4], skull-stripped and intensity normalized. We obtained tumor [5,6] and normal-appearing tissue segmentations [7]. For each subject, we grouped available scans before or after a surgical resection into all possible permutations of three time-points. The data was split into 46:15 patients (3349:90 permutations) for training and testing.We expanded an existing learning-based registration approach [2] to take tumor presence and growth into account. During training, the method estimates the diffeomorphic deformations to the permutation’s mean-space, maximizes the local cross-correlation across the warped images, and encourages a smooth and continuous deformation. To be robust against possible intensity alterations in the tumor region, a loss-function masking strategy was implemented to compute the loss value only in the normal-appearing region across the three time-points. In addition, to register large local mass-effects caused by gliomas, we estimated the deformation at two resolutions, to firstly register the general structures in down-sampled images, and secondly refine the residual deformations at full resolution (Fig. 1).
We evaluated the proposed method against state-of-the-art classical groupwise registration methods: Elastix [8], NiftyReg [9], and ANTs [10]. These were run with default parameters, providing normal tissue masks as input when this option was available (i.e., Elastix and NiftyReg).
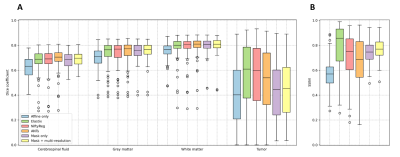
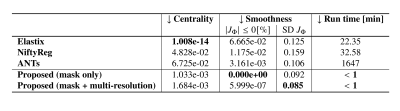
The similarity across the warped images was assessed by the Dice coefficients, and the average structural similarity index measure (SSIM) between warped image and the average image [11]. Also, the centrality was evaluated by the average norm of the three resulting deformations. What is more, the smoothness of the deformations was measured by the number of foldings (negative values) in the Jacobian maps and their average standard deviation [8]. All metrics were computed in the normal-appearing tissue.
Results
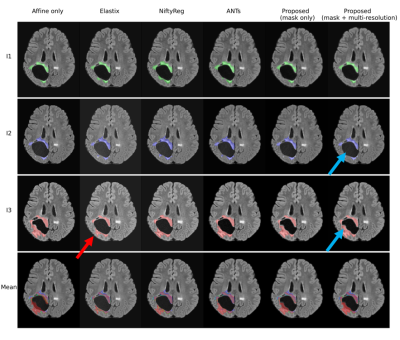
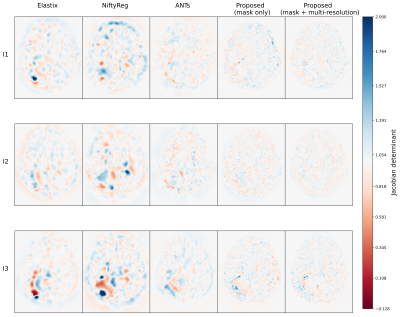
Figure 2 presents the average Dice and SSIM scores of all test permutations by the initial affine registration, the classical methods, and the proposed framework. Our single-stage method (‘mask only’) performed comparably to the classical methods in terms of Dice coefficient. The average SSIM obtained by our method was higher than for these classical methods, except Elastix. On the other hand, our multi-stage implementation (‘mask+multi-stage’) both Dice and SSIM coefficients with respect to the single-stage.Elastix presents the best centrality, followed by our multi-resolution strategy (Table 1). The proposed strategies show improvement in smoothness and have inference runtimes of under a minute, significantly faster than the classical approaches. In a qualitative example (Fig. 4 and Fig. 5), the stronger deformations of Elastix lead to more overlap of the tumor across images, but with non-anatomically plausible deformations near the tumor edge. The proposed methods accurately align the normal-appearing tissue, but did not align the resection volume.
Discussion
The proposed method is able to register glioma images despite the presence of non-correspondences across the time-points by focusing on the normal-appearing tissue similarity. The obtained GM and WM Dice coefficients are comparable to those of state-of-the-art toolboxes, but with higher SSIM values, suggesting that the registrations are more detailed. Elastix and NiftyReg show larger tumor Dice but stronger deformations, which could indicate anatomically implausible registration of non-correspondences. Qualitatively, our method shows stronger misalignment of the resection volume. This could indicate that changes in such volume are identified as non-correspondences instead of mass-effect.Our method also achieves smoother deformations with the least foldings. An important advantage of our network approach is that new images can be registered in seconds, which is much faster than the classical methods (e.g., 28 hours by ANTs). We showed that the multi-stage strategy combined with the tumor masks yields higher registration accuracy than without this strategy, as this allows large, smooth deformations while avoiding local minima. However, for the cases with extremely large mass-effect, further refinement of the method could be considered.
Conclusion
The proposed deep learning-based unbiased group-wise registration method can serve as an alternative to existing classical toolboxes for the analysis of glioma growth in longitudinal MRI.Acknowledgements
We thank the members of the GLASS consortium for providing the used datasets, as well as a clinical insight, and for their comments that greatly improved the manuscript.
We are also grateful for the insightful discussions within the Biomedical Imaging Group Rotterdam (BIGR).
I would particularly like to thank Dr. Frans Vos, Dr. Esther Bron and Dr. Bo Li for their supervision and support during this research, as well as PhD Karin van Garderen for inducing to us this particular challenge and her help during its development.
References
[1] Polfliet, M., Klein, S., Huizinga, W., Paulides, M. M., Niessen, W. J., & Vandemeulebroucke, J. (2018). Intrasubject multimodal groupwise registration with the conditional template entropy. Medical image analysis, 46, 15-25.
[2] Li, B., Niessen, W. J. Klein, S., Ikram, M. A., Vernooij, M. W., & Bron, E. E. (2021, February). Learning unbiased group-wise registration (LUGR) and joint segmentation: evaluation on longitudinal diffusion MRI. In Medical Imaging 2021: Image Processing (Vol. 11596, pp. 136-144). SPIE.
[3] Vallentgoed, W. R., Niers, A., van Garderen, K., Bent, M. V. D., van Dijk, E., Draaisma, K., ... & French, P. (2022). Methylation analysis of matched primary and recurrent IDH-mutant astrocytoma; an update from the GLASS-NL consortium. Cancer Research, 82(12_Supplement), 4020-4020.
[4] Klein, S., Staring, M., Murphy, K., Viergever, M. A., & Pluim, J. P. (2009). Elastix: a toolbox for intensity-based medical image registration. IEEE transactions on medical imaging, 29(1), 196-205.
[5] Kickingereder, P., Isensee, F., Tursunova, I., Petersen, J., Neuberger, U., Bonekamp, D., ... & Maier-Hein, K. H. (2019). Automated quantitative tumour response assessment of MRI in neuro-oncology with artificial neural networks: a multicentre, retrospective study. The Lancet Oncology, 20(5), 728-740.
[6] Isensee, F., Jaeger, P. F., Kohl, S. A., Petersen, J., & Maier-Hein, K. H. (2021). nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nature methods, 18(2), 203-211.
[7] Zhang, Y., Wu, X., Gach, H. M., Li, H., & Yang, D. (2021). GroupRegNet: a groupwise one-shot deep learning-based 4D image registration method. Physics in Medicine & Biology, 66(4), 045030.
[8] Huizinga, W., Poot, D. H., Guyader, J. M., Klaassen, R., Coolen, B. F., van Kranenburg, M., ... & Klein, S. (2016). PCA-based groupwise image registration for quantitative MRI. Medical image analysis, 29, 65-78.
[9] Modat, M., Ridgway, G. R., Taylor, Z. A., Lehmann, M., Barnes, J., Hawkes, D. J., ... & Ourselin, S. (2010). Fast free-form deformation using graphics processing units. Computer methods and programs in biomedicine, 98(3), 278-284.
[10] Avants, B. B., Tustison, N. J., Song, G., Cook, P. A., Klein, A., & Gee, J. C. (2011). A reproducible evaluation of ANTs similarity metric performance in brain image registration. Neuroimage, 54(3), 2033-2044.
[11] Lamprinou, N., Nikolikos, N., & Psarakis, E. Z. (2020). Groupwise Image Alignment via Self Quotient Images. Sensors, 20(8), 2325.
Figures