4326
Fractional-order total variation penalised hyperpolarized metabolic model fitting in the human heart
Jack J. Miller1,2, Justin Y C Lau3, Andrew Lewis4, and Christoffer Laustsen1
1The MR Research Centre, Aarhus University, Aarhus, Denmark, 2OCMR, Radcliffe Department of Medicine, University of Oxford, Oxford, United Kingdom, 3GE Healthcare, Schenectady, NY, United States, 4OCMR, University of Oxford, Oxford, United Kingdom
1The MR Research Centre, Aarhus University, Aarhus, Denmark, 2OCMR, Radcliffe Department of Medicine, University of Oxford, Oxford, United Kingdom, 3GE Healthcare, Schenectady, NY, United States, 4OCMR, University of Oxford, Oxford, United Kingdom
Synopsis
Keywords: Hyperpolarized MR (Non-Gas), Cardiovascular
Fractional-order derivatives represent the smooth analytic continuation of differentiation by a non-integer order. Their use for total-variation spatial regularisation has been proposed as they effectively smoothly interpolate data from the entirety of the image domain, and are reported to avoid ``blocky'' artefacts and better capture edges. Here, we show that their use permits the rapid and parsimonious optimisation of a piecewise metabolic model in the human heart, able to reconstruct terms representing perfusion delay and apparent metabolic rate constants of interconversion.Purpose
Hyperpolarised pyruvate is a metabolic contrast agent translating into the clinic. Many analysis methods have been proposed for hyperpolarised datasets, ranging from integration to the fitting of multidimensional metabolic models.[1] These models aim to overcome limitations in the interpretation of the technique, such as distinguishing regions of high metabolism from rapid tracer washout, or shortened effective $$$T_1$$$. Parametric mapping techniques may also permit dimensionality reduction and greater quantification accuracy across sites. Previous work has shown that mapping can function better in the low SNR environment with spatial regularisation, where regional terms vary smoothly in comparison to noise terms that might be expected to be voxelwise independent.[2]All previous work on this topic has required the metabolic model fitted to be expressed in terms of a linear operator, so that the adaptive-method-of-multipliers (ADMM) can be used for solving the resulting multidimensional optimisation problem. This constraint implies the use of a spatially homogeneous kinetic model.[1,3] For cardiac applications, this is inappropriate as pyruvate spatially enters the ventricles first, and most modelling approaches estimate an AIF from them, rather than assuming that tissue is perfused in each voxel, as would be required by a linear model.
In this work, we propose two major developments to regularised fitting: (1) extending the spatial regularisation term to fractional-order total variation, appropriate for the sparse nature of the images seen; and (2) the use of spatially inhomogeneous models with an arterial input function derived from the LV cavum. We demonstrate our results in the healthy human heart.
Methods
Constrained parametric mapping solves a multidimensional minimisation problem of the form$$\text{argmin}_{\vec{\theta}}\left\{{\vert\vert\hat{d}(x_i,y_i,m_i,t_i)-g(\vec{\theta}(x_i,y_i),\,t_i)\vert\vert_{2}}+\lambda\,r(\vec{\theta})\right\}$$
where acquired spatially/temporally varying data $$$\hat{d}(x_i,y_i,m_i,t_i)$$$ from metabolite $$$m$$$ is described by a model, i.e., a function of a set of parameters that both contain a scalar component and vary in space, $$$\vec{\theta}(x_i,y_i)$$$, evaluated at the same timepoints (and for the same metabolites) as the data.
As parameters are spatially correlated, one approach is to introduce regularising term(s) onto the above, i.e. $$$\lambda{}r(\vec{\theta})$$$, to enhance spatial consistency. This approach is conceptually similar to `kriging' as performed in geospatial science. Total variation has been previously used for linear hyperpolarised metabolic models, i.e. $$$r(\vec{\theta})=||\nabla\theta||_1$$$. However, this is prone to both ``blocking'' artefacts and can result in over-smoothing. Fractional-order total variation approaches, in which the laplacian of order $$$\alpha, \quad \nabla_\alpha{}\vec{\theta}$$$ is used instead, are reported to preserve edges whilst avoiding over-regularising and the appearance of correlated noise within a block.[4,5] This can be thought intuitively as arising from the fact that, rather than being computed via finite differences, a gamma-variate interpolant, weighted to data around the difference in question but with global scope, is used.
Here, we used fractional-order total variation of order $$$\alpha=1.9$$$ to fit a modified metabolic model following that of Zierhut[3] to human heart data, i.e. $$$r=||\nabla_{1.9}(\vec{\theta})||$$$. This model is an analytic piecewise linear representation of the hyperpolarised experiment: pyruvate is injected linearly, decays (T1 and metabolism), and other downstream metabolites are produced according to first-order chemical kinetics. The concentrations at the boundaries of the temporal regions are set by continuity. It is:
$$\begin{align}g^\text{Pyr}(t)&\propto\begin{cases}0&t<t_a\\\frac{R_i}{k_\text{Pyr}}\left(1-e^{-k_\text{Pyr}(t-t_a)}\right)&t\in{}[t_a,\,t_e]\\M_{\text{Pyr}}e^{-k_\text{Pyr}(t-te)}&t>t_e\end{cases}\\g^{X\neq\text{Pyr}}&\propto\begin{cases}0&t-t_d<t_a\\\frac{k_{\text{Pyr}X}\cdot{}R_i}{k_\text{Pyr}-k_X}\left[\frac{1-e^{-k_X(t-t_a)}}{k_X}-\frac{1-e^{-k_\text{Pyr}(t-t_a)}}{k_\text{Pyr}}\right]&t-t_d\in{}[t_a,\,t_e]\\\frac{M_{\text{Pyr}}\cdot{}k_{\text{Pyr}\,X}}{k_\text{Pyr}-k_X}\left[e^{-k_X(t-t_e)}-e^{-k_\text{Pyr}(t-t_e)}\right]+M_{X}e^{-k_X(t-te)}&t-t_d>t_e\\\end{cases}\end{align}$$
where $$$t_a,\,t_e$$$ represents the start/end of the injection of pyruvate; $$$k_\text{Pyr}$$$ the apparent decay constant of pyruvate due to $$$T_1$$$ and flip angle depletion; $$$k_X$$$ that for metabolite $$$X$$$; $$$k_{\text{Pyr}\, X}$$$ the metabolic rate constant between pyruvate and $$$X$$$; and $$$t_d$$$ perfusion delay.
Hyperpolarised cardiac images were obtained by spectral-spatial excitation and constant-density spiral readout from a healthy human volunteer, and the LV cavum manually segmented. Initial parameter estimates for the pyruvate model were determined via least-squares. We introduce an indicator function $$$\Xi(x,\,y)\in[0,\max(\text{Pyr})]$$$, distinguishing between signal/noise and converting between ADC units and maximum pyruvate signal. The resulting minimisation problem was solved (in MATLAB) with no spatial regularisation term as an initial condition, and subsequently via a global-optimisation simulated-annealing algorithm on the Arcus-C supercomputer.
Results
Given data of high SNR (Fig.1), we were able to obtain good fits with the Zierhut model to the data (Fig.2) in the LV cavum and elsewhere across the heart. Local, voxelwise independent optimisation was quick to converge but with several voxels dominated by noise. The full spatially constrained model took approximately 19 hours to solve (on 24$$$\times$$$96 cores). However, we observed excellent fits with a significantly reduced total AIC and the complete amelioration of noise voxels with no appreciable change in other constants. The method was effectively able to map out regions of signal from regions of noise (Fig.3) and minimised variation due to coil profile effects.Discussion and Conclusion
As hyperpolarised MR translates to the clinic, the ability to locate spatial heterogeneity in disease is likely to become paramount. Parametric mapping may be able to distinguish sources of biological variation from that due to e.g. coil profile effects. We have shown the ``brute-force'' spatially regularised fitting of an advanced hyperpolarised metabolic model to a high-quality dataset and the reconstruction of physiologically plausible parameters, such as a delay of approximately 6 seconds between the first arrival of pyruvate and the first production of bicarbonate. Future work will both aim to significantly speed up this approach, compute further statistics that address questions about parsimony, and validate its use in a larger cohort.Acknowledgements
JJM would like to acknowledge a Novo Fonden grant, ref. NNF21OC0068683.References
[1] C. J. Daniels, M. A. McLean, R. F. Schulte, F. J. Robb, A. B. Gill, N. McGlashan, M. J. Graves, M. Schwaiger, D. J. Lomas, K. M. Brindle, F. A. Gallagher, NMR Biomed. 2016, 29, 387–399.[2] J. Maidens, J. W. Gordon, H.-Y. Chen, I. Park, M. Van Criekinge, E. Milshteyn, R. Bok, R. Aggarwal, M. Ferrone, J. B. Slater, J. Kurhanewicz, D. B. Vigneron, M. Arcak, P. E. Z. Larson, IEEE Transactions on Medical Imaging 2018, 37, 2603–2612.[3] M. L. Zierhut, Y.-F. Yen, A. P. Chen, R. Bok, M. J. Albers, V. Zhang, J. Tropp, I. Park, D. B. Vigneron, J. Kurhanewicz, R. E. Hurd, S. J. Nelson, J. Magn. Reson. 2010, 202, 85–92.[4] Y. Zhang, W. Zhang, Y. Lei, J. Zhou, Journal of the Optical Society of America. A Optics Image Science and Vision 2014, 31, 981–995.[5] D. Chen, Y. Chen, D. Xue, Applied Mathematics and Computation 2015, 257, 537–545.Figures

The high-quality, high-SNR human hyperpolarised cardiac imaging dataset analysed here. Pyruvate can be observed perfusing the cardiac chambers at anatomically correct times prior to the production of the downstream metabolic product of interest, bicarbonate
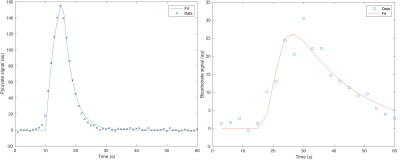
Segmented LV cavum and corresponding pyruvate fit: good agreement between the model and the data was observed. Similarly, shown is a representative mid-ventricle voxelwise fit for bicarbonate signal.
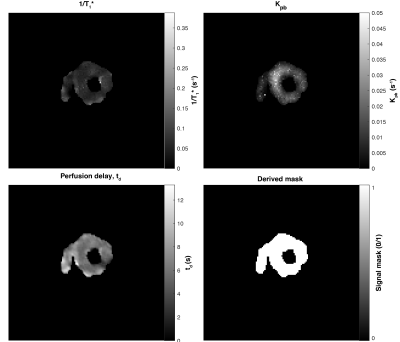
Derived parameters from fitting the human hyperpolarised dataset shown. Here, $$$1/T_1*$$$ represents the effective rate constant due to RF excitation and $$$T_1$$$ decay; $$$k_{pb}$$$ is the first-order rate constant between pyruvate and lactate, $$$t_d$$$ a perfusion delay and the derived mask indicates regions of expected signal.
DOI: https://doi.org/10.58530/2023/4326