4317
On the practical influence of extra-axonal heterogeneity in a numerically informed model of extra-axonal water diffusion
Kevin D Harkins1,2,3, Junzhong Xu1,2, John C Gore1,2,3, and Mark D Does2,3
1Radiology and Radiological Sciences, Vanderbilt University Medical Center, Nashville, TN, United States, 2Institute of Imaging Science, Vanderbilt University Medical Center, Nashville, TN, United States, 3Biomedical Engineering, Vanderbilt University, Nashville, TN, United States
1Radiology and Radiological Sciences, Vanderbilt University Medical Center, Nashville, TN, United States, 2Institute of Imaging Science, Vanderbilt University Medical Center, Nashville, TN, United States, 3Biomedical Engineering, Vanderbilt University, Nashville, TN, United States
Synopsis
Keywords: Simulations, Microstructure
This study explores the role of extra-axonal environment on the time dependent diffusion coefficient of extra-axonal water in white matter. Monte Carlo simulations of water diffusion in geometries with varying extra-axonal heterogeneity were compared with a proposed analytic model. The results agree with previously published power-law relationships that depend on structural order, but also uncovers trends between model parameters with characteristics of extra-axonal space.Introduction
There is continuing debate over the microstructural features of white matter that influence the variations observed in apparent diffusion coefficients with diffusion time. Most often, white matter is modeled as the sum of signals from separate compartments1, especially intra-axonal and extra-axonal water, which are treated as non-exchanging compartments. While several analytic models exist for intra-axonal signal, extra-axonal water diffusion has been less well characterized2,3. Several models have treated extra-axonal water diffusion as constant with diffusion time. Others model the approach to the long-diffusion time limit in terms of a power law behavior4, or $$$D_\mathrm{inst}(t)\approx D_\infty + k t^{-\theta}$$$, where $$$D_\mathrm{inst}$$$ is the instantaneous diffusion coefficient and $$$k$$$ is a constant. The exponent, $$$\theta$$$, depends upon the characteristics of the diffusion geometry, both in dimensionality and structural order. However, this model is unbounded, and the range of diffusion times for which this model is valid is often unclear. This study explores a bounded and closed form approximation to $$$D_\mathrm{inst}(t)$$$, and uses numeric simulations to evaluate how water diffusion is affected by the characteristics of extra-axonal space, especially heterogeneous packing of axons.Methods
We propose an analytic form for the dispersion of extra-axonal diffusion,$$D_\mathrm{inst,e}(t) = D_\infty + \frac{D_0 - D_\infty}{1+(t/t_\mathrm{e})^\theta},$$
which is illustrated in the top panel of Figure 1. In contrast to analytic approximations to diffusion at short5,6 and long times scales4, this form is bounded between $$$D_0$$$ and $$$D_\infty$$$ for all $$$t\ge0$$$ , and disperses with a characteristic time constant $$$t_\mathrm{e}$$$.The exponent of the power law can be different in the short and long diffusion time regimes, so $$$\theta$$$ is also allowed to vary with diffusion time, such that $$$\theta_0$$$ is the exponent power for the short diffusion time regime, and $$$\theta_\infty$$$ is the power law for the long diffusion time regime. The time dependent diffusion coefficient is calculated as
$$D(t) = \frac{1}{t} \int_0^t D_\mathrm{inst}(t') dt'.$$
Monte Carlo diffusion simulations were performed in the extra-axonal space of 2D arenas of 500 axons. Distributions of axon diameters were drawn from a `lognormal` probability density. Eight simulation geometries were created with unit axon diameter (=1$$$\mu$$$m) for all combinations: extra-axonal volume fraction, $$$v_\mathrm{e}$$$ = 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8; standard deviation of the log-spaced diameters, $$$\sigma$$$ = 0.3, 0.5 and 0.7; extra-axonal heterogeneity, $$$\alpha$$$ = 0, 0.2, 0.4, 0.6, 0.8, and 1.0. Geometries varying extra-axonal heterogeneity were created by increasing the strength of repulsive forces between axons, similar to those of an electrostatic field. One example set of simulation geometries with varying extra-axonal heterogeneity is shown in Figure 2, where $$$\alpha=0$$$% represents heterogeneous spacing of axons and $$$\alpha=100$$$% represents homogeneous spacing of axons. Simulations of the mean squared displacement in the radial diffusion direction were performed for each simulation geometry, and the time dependent diffusion coefficient was calculated as $$$D(t)=\left<x^2\right>/(2t)$$$. Simulated $$$D(t)$$$ was fit to Equations 1 and 2 above for $$$D_\infty$$$, $$$t_\mathrm{e}$$$, $$$\theta_0$$$ and $$$\theta_\infty$$$.
Results
Representative $$$D(t)$$$ from simulations with $$$v_\mathrm{e}=0.3$$$ and $$$\sigma=0.5$$$ are shown in Figure 3, where the colors highlight the influence of extra-axonal heterogeneity, $$$\alpha$$$. The eight individual simulations are shown as thin lines, with a thick line representing the fit to the average of those simulations designed with the same characteristics. While extra-axonal heterogeneity has little or no influence on $$$D(t)$$$ in the short diffusion time limits, it has significant influence on the long diffusion time behavior of $$$D(t)$$$.Figure 4 plots the fitted model parameters vs parameters of the generated simulation geometries, where general trends in the data are highlighted with a thick line through the average of the simulated results. Notably, $$$D_\infty$$$ did not depend on $$$\sigma$$$, but increased with $$$v_\mathrm{e}$$$ and $$$\alpha$$$. $$$t_\mathrm{e}$$$ generally increased with both $$$\sigma$$$ and $$$v_\mathrm{e}$$$, but decreased with $$$\alpha$$$. $$$\theta_\infty$$$ tended upwards in simulation geometries with extra-axonal spaces that appeared less heterogeneous, that is with lower $$$\sigma$$$, higher $$$v_\mathrm{e}$$$, and higher $$$\alpha$$$. Finally, $$$\theta_0$$$ was mostly insensitive to all changes in extra-axonal geometry.
Discussion and Conclusion
This work agrees with and extends several previous studies investigating the role of structural disorder on the diffusion time dependence of extra-axonal diffusion. For instance, prior studies indicate highly ordered extra-axonal spaces should exhibit a long diffusion-time limited power law with $$$\theta=1$$$. In this work, $$$\theta_\infty$$$ increases towards 1 in geometries that tend towards more structural order: i.e. geometries with more uniform axon diameter (low $$$\sigma$$$), higher extra-axonal volumes (high $$$v_\mathrm{e}$$$), and with homogeneous axonal spacing (high $$$\alpha$$$).This study also suggests that significant structural information is present in extra-axonal diffusion, even when structural disorder is present. For example, the parameters $$$t_\mathrm{e}$$$ and $$$D_\infty$$$ depend strongly on $$$v_\mathrm{e}$$$ and $$$\alpha$$$—even in regions where extra-axonal heterogeneity is high. Future studies should explore the use of numerically informed analytic models to explore the role of extra-axonal diffusion in the time dependent diffusion coefficient measured in white matter.
Acknowledgements
This work is supported by NIH R01EB031954.References
1. Panagiotaki, E., Schneider, T., Siow, B., Hall, M. G., Lythgoe, M. F., & Alexander, D. C. (2012). Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison. NeuroImage, 59(3), 2241–2254. https://doi.org/10.1016/j.neuroimage.2011.09.0812. Lam, W. W., Jbabdi, S., & Miller, K. L. (2014). A model for extra-axonal diffusion spectra with frequency-dependent restriction. Magnetic Resonance in Medicine, 73(6), 2306–2320. https://doi.org/10.1002/mrm.25363
3. Burcaw, L. M., Fieremans, E., & Novikov, D. S. (2015). Mesoscopic structure of neuronal tracts from time-dependent diffusion. NeuroImage, 114, 18–37. https://doi.org/10.1016/j.neuroimage.2015.03.061
4. Novikov, D. S., Jensen, J. H., Helpern, J. A., & Fieremans, E. (2014). Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences of the United States of America, 111(14), 5088–5093. https://doi.org/10.1073/pnas.1316944111
5. Mitra, P. P., Sen, P. N., Schwartz, L. M., & Le Doussal, P. (1992). Diffusion propagator as a probe of the structure of porous media. Physical Review Letters, 68(24), 3555–3558. https://doi.org/10.1103/PhysRevLett.68.3555
6. Novikov, D. S., & Kiselev, V. G. (2011). Surface-to-volume ratio with oscillating gradients. Journal of Magnetic Resonance, 210(1), 141–145. https://doi.org/10.1016/j.jmr.2011.02.011
Figures
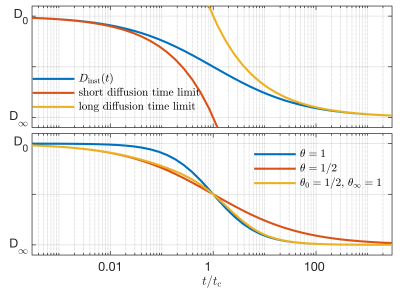
Figure 1: Top: The proposed analytic model for $$$D_\mathrm{inst}(t)$$$ is bounded for all $$$t\ge0$$$, and can agree with short and long diffusion time limited cases. Bottom: Since the power law exponent can vary in the short and long diffusion time limits, $$$\theta$$$ similarly disperses with $$$t$$$, providing $$$\theta_0$$$ in the short diffusion time limit, and $$$\theta_\infty$$$ in the long diffusion time limit.
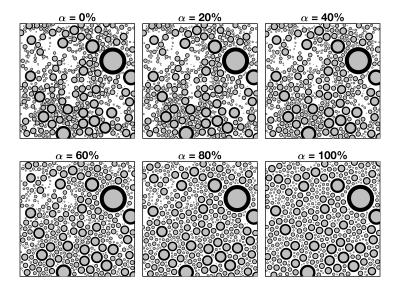
Figure 2: The six example geometries illustrate the transition of heterogeneous to homogenous spacing of axons.The parameter $$$\alpha$$$ specifies the heterogeneity of extra-axonal space, where $$$\alpha=0$$$% is heterogeneous spacing between axons, and $$$\alpha=100$$$% is equal spacing between axons.
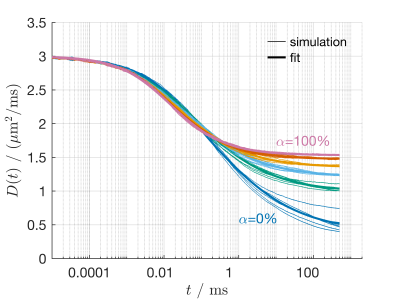
Figure 3: Representative $$$D(t)$$$ from Monte Carlo simulations (thin lines) and model fits (thick lines) with $$$v_\mathrm{e}=0.3$$$ and $$$\sigma=0.5$$$ and varying extra-axonal heterogeneity, given as $$$\alpha$$$. Extra-axonal heterogeneity significantly impacts the behavior of diffusion in the long diffusion time regime.
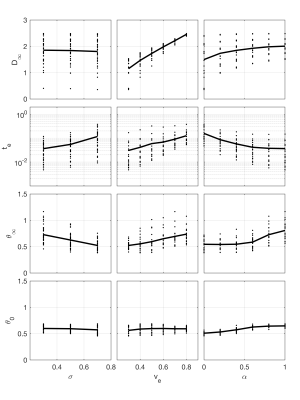
Figure 4: Fitted parameters of the analytic model ($$$D_\infty$$$, $$$t_\mathrm{e}$$$, $$$\theta_\infty$$$, and $$$\theta_0$$$) as a function of simulation geometry parameters. Thick lines represent the trend of the mean of the fitted parameters.
DOI: https://doi.org/10.58530/2023/4317