4307

A general quantitative diffusion MRI model of water exchange, confinement, and hindrance with arbitrary gradient waveform encoding

Sisi Li¹, Diwei Shi², Xiaoyu Jiang^3,4, Li Chen², Quanshui Zheng², Hua Guo¹, and Junzhong Xu^3,4,5,6
¹Center for Biomedical Imaging Research, Tsinghua University, Beijing, China, ²Center for Nano and Micro Mechanics, Department of Engineering Mechanics, Tsinghua University, Beijing, China, ³Institute of Imaging Science, Vanderbilt University Medical Center, Nashville, TN, United States, ⁴Department of Radiology and Radiological Sciences, Vanderbilt University Medical Center, Nashville, TN, United States, ⁵Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, ⁶Department of Physics and Astronomy, Vanderbilt University, Nashville, TN, United States

Synopsis

Keywords: Signal Modeling, Microstructure

This study proposed and validated a general diffusion MRI biophysical model enabling simultaneous estimation of cell size, intracellular volume fraction, and transcytolemmal water exchange. The model introduces two-mode intracellular diffusion, corrects for restriction-induced “edge-enhancement” effect, and handles arbitrary diffusion gradient waveforms. The results of both in silico and in vitro experiments suggest this model not only improves the accuracy of estimated microstructural parameters such as cell size but also provides reasonable estimates of water exchange rate constant that is usually ignored previously. Such a comprehensive model may have potential to probe tumor status more precisely which is feasible in clinics.

Introdcution

Numerous multi-compartment biophysical models ^1-12 have been developed for quantitative diffusion MRI (dMRI) to characterize cellular microstructures. However, these models usually ignore transcytolemmal water exchange ¹³, i.e., the water exchange across cell membranes, leading to misestimates of microstructural parameters such as cell size ($$$d$$$) and intracellular volume fraction ($$$v_{in}$$$).
Meanwhile, Kӓrger model-based methods ^14-17 have been proposed to estimate transcytolemmal water exchange with assumptions on pulse sequence, diffusion time, and exchange rate. Nevertheless, these methods usually overestimate transcytolemmal water exchange rate constant ($$$k_{in}$$$) due to restriction-induced “edge-enhancement effect” ¹⁸.
A few attempts have tried to unify the above two separate frameworks to a more comprehensive biophysical model, such as the work based on strong assumptions on short-pulse approximation ^19,20 and very recent work ²¹ based on cumulant expansion of the signal attenuation.
In this study, we proposed a general quantitative diffusion MRI model of water exchange, confinement, and hindrance with arbitrary gradient waveform encoding (EXCHANGE). This EXCHANGE model introduces two-mode intracellular diffusion to account for exchange, corrects for restriction-induced edge-enhancement effect, and handles arbitrary gradient waveforms. Both in-silico and in-vitro experiments were performed to evaluate the accuracy and precision of fitted microstructural parameters such as $$$d$$$, $$$v_{in}$$$, and $$$k_{in}$$$.

Theory

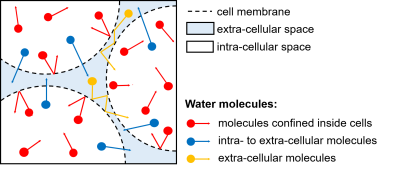
Two-mode intracellular diffusion
As shown in Fig. 1, during a short time interval, an intracellular water molecule has a probability of $$$p$$$ crossing the membrane (exchange) and hence $$$(1-p)$$$ staying inside the cell (confined). This effectively divides intracellular water diffusion into two modes: restricted (mode A) and hindered (mode B). Therefore, the two-mode intracellular diffusion coefficient can be defined as: $$$D^*_{in}=-1/b*ln((1-p)exp(-bADC_r)+pexp(-bD_{inh}))$$$, where $$$ADC_r$$$ is the apparent restricted diffusion coefficient and $$$D_{inh}$$$ represents an averaged hindered diffusivity of mode B. We empirically compute $$$D_{inh}$$$ by: $$$D_{inh}=v_{in}((1-p)ADC_r+pD_{in})+v_{ex}D_{ex}$$$, where $$$v_{in}$$$ and $$$v_{ex}$$$ are the volume fractions and $$$v_{in}+v_{ex}=1$$$, $$$D_{ex}$$$ is the hindered diffusion coefficient of the extracellular compartment. Note that we can find: $$$p=0.75R/sqrt(2D_{in}τ_{in})$$$, where $$$R$$$ is the cell radius, $$$τ_{in}$$$ is the mean intracellular pre-exchange lifetime, and $$$D_{in}$$$ is the intracellular diffusion coefficient without the influences of cell membranes.
For simplification, we only define an effective $$$D_{ex}$$$ to describe the overall extracellular hindered diffusion due to the very narrow interstitial space.
Correction for the restriction-induced edge-enhancement effect
One long-time overlooked problem is that Kӓrger model-based methods might overestimate the water exchange rate since exchange rate constants of magnetizations, $$$k^m_{in(ex)}$$$, are larger than exchange rate constants of water molecules, $$$k_{in(ex)}$$$ due to restriction-induced “edge-enhancement” effect. In this work, we correct for such a bias by defining $$$k^m_{in}=αk_{in}$$$, where $$$α$$$ is the correction factor greater than 1, and we empirically give out $$$α=1+2v_{in}R/sqrt(2D_{in}τ_{in})$$$; $$$k^m_{ex}≈k_{ex}$$$ because the extracellular space is a narrow interstitial space where the edge-enhancement effect can be ignored.
Based on the above work and the generalized method ²² to calculate $$$ADC_r$$$ under arbitrary gradient waveforms, we propose the EXCHANGE model. The corresponding analytical expression can be derived in a form similar to the solution of the classical Kӓrger model.

Methods

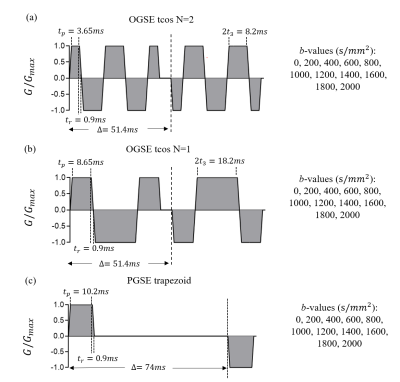
Numerical simulations
A finite difference method was used to simulate dMRI signals based on a tightly packed, spherical cells on a face-centered-cubic lattice with $$$v_{in}=$$$51%, $$$D_{in}=1.58 μm^2/ms$$$ and $$$D^{free}_{ex}=2 μm^2/ms$$$. The cell diameter $$$d$$$ was 8~18 μm. $$$τ_{in}$$$ was set as 50, 70, 100, 200, 400 and $$$\infty$$$ ms. Diffusion sequences and parameters are shown in Fig. 2. Fitting was repeated 100 times each with Rician noise corresponding to SNR=45. The value of $$$D_{in}$$$ was fixed as $$$1.58 μm^2/ms$$$ so unknown parameters are $$$v_{in}$$$, $$$d$$$, $$$k$$$ (note: $$$k=1/τ_{in}$$$) and $$$D_{ex}$$$. The IMPULSED ²³ and JOINT ¹⁹ models were also performed to compare with the EXCHANGE model.
Restrospective cell experiments
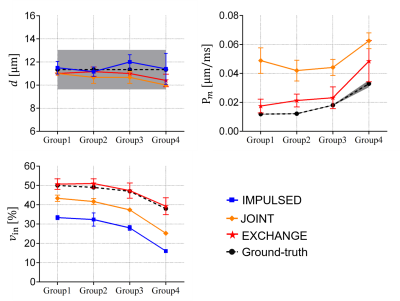
The details of the in-vitro experiment have been reported previously ²⁴. Briefly, fixed MEL cells were treated with different concentrations of saponin to form four groups. The cell pellet samples were scanned using an Agilent 4.7 Tesla MRI scanner with a maintained temperature. IMPULSED, JOINT, and EXCHANGE models were used and then compared with the light microscopy-derived $$$d$$$ and the constant gradient (CG) method-derived cell membrane permeability $$$P_m$$$ (note: $$$1/P_m=6τ_{in}/d-d/10D_{in}$$$) ²⁵.

Results and Discussion

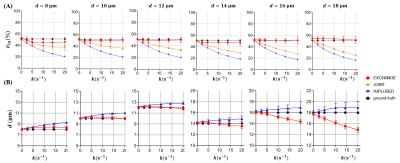
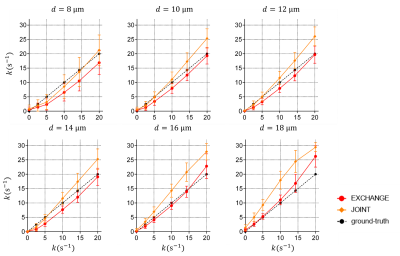
Fig. 3 shows the fitting results of $$$v_{in}$$$ and $$$d$$$. The IMPULSED and JOINT models underestimate $$$v_{in}$$$ and the bias increases with faster water exchange, i.e., larger $$$k$$$. By contrast, the EXCHANGE model provides the most accurate results, and the fitted $$$v_{in}$$$ matches the ground-truth well for $$$10 μm≤d≤18 μm$$$. In Fig. 3B , the IMPULSED model usually overestimates $$$d$$$. The results of the JOINT and EXCHANGE models match the ground-truth well for $$$d≤14 μm$$$ although both models underestimate $$$d$$$ for larger diameters.
Fig. 4 shows the fitting results of $$$k$$$. The JOINT model overestimates $$$k$$$ for $$$d≥10 μm$$$. The results fitted by the EXCHANGE model are closer to the ground-truth except for $$$d=8 μm$$$.
Fig. 5 shows that the EXCHANGE model can extract more accurate and more comprehensive microstructure information of cell tissues in the cell experiments.

Conclusion

The proposed EXCHANGE model not only enables simultaneous estimation of cell size, intracellular volume fraction, and membrane permeability but also improves the accuracy of estimated microstructural parameters compared with other methods. This is promising to probe tumor status more precisely and assist personalized medicine in cancer clinics.

Acknowledgements

No acknowledgments are found.

References

1. Gore JC, Xu J, Colvin DC, Yankeelov TE, Parsons EC, Does MD. Characterization of tissue structure at varying length scales using temporal diffusion spectroscopy. NMR in Biomedicine 2010;23(7):745-756.

2. Novikov DS, Fieremans E, Jespersen SN, Kiselev VG. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR in Biomedicine 2019;32(4):e3998.

3. Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 2012;61(4):1000-1016.

4. Kaden E, Kelm ND, Carson RP, Does MD, Alexander DC. Multi-compartment microscopic diffusion imaging. Neuroimage 2016;139:346-359.

5. Novikov DS, Veraart J, Jelescu IO, Fieremans E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. Neuroimage 2018;174:518-538.

6. Alexander DC, Hubbard PL, Hall MG, et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage 2010;52(4):1374-1389.

7. Palombo M, Ianus A, Guerreri M, et al. SANDI: A compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. Neuroimage 2020;215:116835.

8. Jiang X, Xu J, Gore JC. Mapping hepatocyte size in vivo using temporal diffusion spectroscopy MRI. Magnetic Resonance in Medicine 2020;84(5):2671-2683.

9. Panagiotaki E, Walker-Samuel S, Siow B, et al. Noninvasive Quantification of Solid Tumor Microstructure Using VERDICT MRI. Cancer Research 2014;74(7):1902-1912.

10. Jiang X, Li H, Xie J, Zhao P, Gore JC, Xu J. Quantification of cell size using temporal diffusion spectroscopy. Magnetic Resonance in Medicine 2016;75(3):1076-1085.

11. Reynaud O, Winters KV, Hoang DM, Wadghiri YZ, Novikov DS, Kim SG. Pulsed and oscillating gradient MRI for assessment of cell size and extracellular space (POMACE) in mouse gliomas. NMR in Biomedicine 2016;29(10):1350-1363.

12. Jiang X, Li H, Xie J, et al. In vivo imaging of cancer cell size and cellularity using temporal diffusion spectroscopy. Magnetic Resonance in Medicine 2017;78(1):156-164.

13. Li H, Jiang X, Xie J, Gore JC, Xu J. Impact of transcytolemmal water exchange on estimates of tissue microstructural properties derived from diffusion MRI. Magnetic resonance in medicine 2017;77(6):2239-2249.

14. Price WS, Barzykin AV, Hayamizu K, Tachiya M. A Model for Diffusive Transport through a Spherical Interface Probed by Pulsed-Field Gradient NMR. Biophysical Journal 1998;74(5):2259-2271.

15. Stanisz GJ, Li JG, Wright GA, Henkelman RM. Water dynamics in human blood via combined measurements of T2 relaxation and diffusion in the presence of gadolinium. Magnetic Resonance in Medicine 1998;39(2):223-233.

16. Lätt J, Nilsson M, van Westen D, Wirestam R, Ståhlberg F, Brockstedt S. Diffusion-weighted MRI measurements on stroke patients reveal water-exchange mechanisms in sub-acute ischaemic lesions. NMR in Biomedicine 2009;22(6):619-628.

17. Karger J, Pfeifer H, Heink W. Principles and applications of self-diffusion measurements by nuclear magnetic resonance. In: Waugh JS, editor. Advances in Magnetic Resonance. Volume 12. 1250 Sixth Avenue San Diego, California 92101: Academic Press, Inc.; 1988. p 1-89.

18. Sukstanskii AL, Ackerman JJH, Yablonskiy DA. Effects of barrier-induced nuclear spin magnetization inhomogeneities on diffusion-attenuated MR signal. Magnetic Resonance in Medicine 2003;50(4):735-742.

19. Jiang X, Devan SP, Xie J, Gore JC, Xu J. Improving MR cell size imaging by inclusion of transcytolemmal water exchange. NMR in Biomedicine 2022:e4799.

20. Stanisz GJ, Wright GA, Henkelman RM, Szafer A. An analytical model of restricted diffusion in bovine optic nerve. Magnetic Resonance in Medicine 1997;37(1):103-111.

21. Chakwizira A, Westin C-F, Brabec J, et al. Diffusion MRI with pulsed and free gradient waveforms: Effects of restricted diffusion and exchange. NMR in Biomedicine 2022:e4827.

22. Shi D, Li S, Chen L, Zheng Q, Guo H, Xu J. An efficient approach for fast signal computation of restricted diffusion with arbitrary gradient waveforms. Proceedings of the International Society of Magnetic Resonance in Medicine, London, 2022. P4752

23. Xu J, Jiang X, Li H, et al. Magnetic resonance imaging of mean cell size in human breast tumors. Magnetic Resonance in Medicine 2020;83(6):2002-2014.

24. Li H, Jiang X, Xie J, Gore JC, Xu J. Impact of transcytolemmal water exchange on estimates of tissue microstructural properties derived from diffusion MRI. Magnetic resonance in medicine 2017;77(6):2239-2249.

25. Stepisnik J. Time-dependent self-diffusion by NMR spin-echo. Physica B 1993;183(4):343-350.

Figures

Fig. 1 Graphic illustrations of three different cases for water molecule diffusion movement in intra- and extracellular spaces.

Fig. 2 Different gradient waveforms used in the numerical simulations. (a). cosine-modulated trapezoidal OGSE acquisitions with N=2 (tcos N=2) (b). cosine-modulated trapezoidal OGSE acquisitions with N=1 (tcos N=1) (c). trapezoid-shaped PGSE acquisitions.

Fig. 3 (A) Intracellular volume fraction $$$v_{in}$$$ and (B) voxel-wise mean cell size $$$d$$$, fitted by the IMPLUSED, JOINT, and the proposed EXCHANGE model, respectively, as a function of $$$k$$$ in the numerical simulations.

Fig.4 Transcytolemmal Water exchange rate constant $$$k$$$ fitted by the IMPLUSED, JOINT, and EXCHANGE model, respectively, as a function of $$$k$$$ (ground-truth) in the numerical simulations.

Fig.5 Results from the IMPLUSED, JOINT and EXCHANGE model in the four groups of in-vitro cell experiments. The shaded area indicates STD of light-microscopy obtained cell sizes.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

4307

DOI: https://doi.org/10.58530/2023/4307