Synopsis

Keywords: Myocardium, Microstructure

The objective of this work was to control the total number of collected diffusion weighted images (DWI) across several different acquisition schemes to evaluate which combination of directions and averages provides the highest quality data. In vivo cDTI data was collected in volunteers (N=5) using a series of fixed duration protocols that span a range of diffusion directions and signal averages. We found that balancing the number of diffusion directions (12-20) and averages (5-3) allows for robust quantification of mean diffusivity, fractional anisotropy, and helix measurements in a fixed scan time.

Introduction

Cardiac diffusion tensor imaging (cDTI) is a non-invasive imaging technique used to estimate the underlying microstructural features of the heart [1-3]. cDTI is useful for confirming myocardial microstructural changes for serval cardiac pathologies [4]. Unfortunately, cDTI requires a prolonged scan time due to the low signal-to-noise ratio (SNR) and the number of diffusion encoding directions necessary to perform an accurate DTI reconstruction. To overcome low SNR, multiple averages are acquired, which further prolongs the scan time. In addition, increasing the number of diffusion directions allows for a better estimation of the tensor, but at the cost of prolonging the scan time. The objective of this work was to control the total number of collected diffusion-weighted images (DWI) across several different acquisition schemes to evaluate which combination of directions and averages provides the highest quality data.

Methods

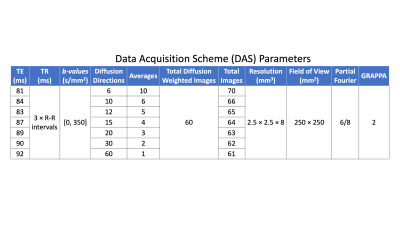
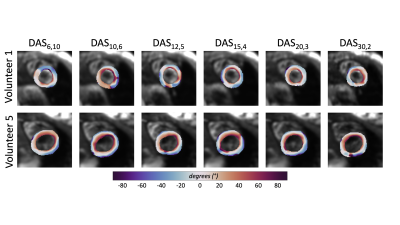
Five healthy volunteers (26.8±4.2 years) were imaged (IRB approved, consented) at 3T (Skyra, Siemens) to obtain a mid-ventricular slice of the heart. A free-breathing, ECG-gated, M₁+M₂-compensated spin echo EPI cDTI sequence [2] was used to acquire cDTI datasets for six different data acquisition schemes (DAS), which include different combinations of diffusion directions and averages, totaling to 60 DWI per acquisition. An overview of the scanning parameters can be seen in Table 1. The only differences between each acquisition are the number of diffusion encoding directions (N_dir) and the number of averages (N_avg) acquired. Data acquisition schemes (DAS_dir,avg) are identified with the number of directions and averages: DAS_6,10, DAS_10,6, DAS_12,5, DAS_15,4, DAS_20,3, DAS_30,2. The acquired diffusion encoding directions were created using an electrostatic repulsion algorithm [5] to provide data acquisition schemes with low condition numbers [6]. For each DAS, the echo time was minimized to provide optimal SNR for a given scheme. All datasets were processed through a custom Python pipeline that included Gibb’s ringing removal, acquisition rejection, affine image registration, signal averaging, denoising, and interpolation. Datasets were evaluated on several metrics, the first being voxel-wise SNR maps. Quantitative cDTI metrics of mean diffusivity (MD) and fractional anisotropy (FA), were compared across all subjects (median, 1^st quartile, 3^rd quartile). Helix angle (HA) maps were generated across all subjects for qualitative assessment.

Results

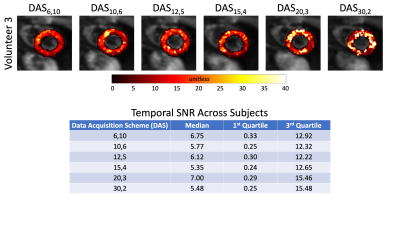
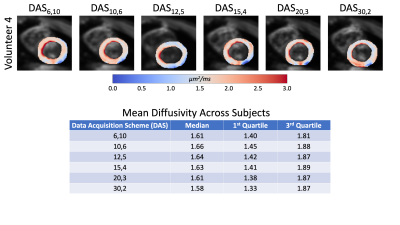
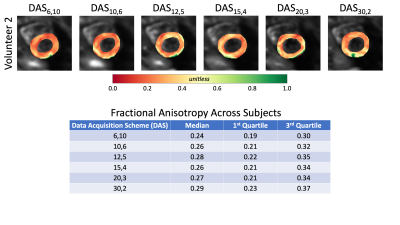
Temporal SNR maps and statistics for the b=0 images can be seen in Figure 1. Larger interquartile ranges are apparent as the number of averages increases, but the median SNR was relatively similar across DAS. The expected trend of decreasing SNR as the number of averages decreased was not observed. Quantitative MD maps can be seen in Figure 2 and displayed minimal variations for both the medians and interquartile intervals across DAS. Quantitative FA maps displayed minimal variations for both the medians and interquartile intervals across DAS (Figure 3). Qualitative HA maps display more accurate results when a compromise of angular sensitivity and averages are obtained (Figure 4). Examples of this include DAS_12,5, DAS_15,4, and DAS_20,3.

Discussion

A number of factors could impact the not observed trend of increasing SNR as the number of averages increased for the b=0 images. Due to the nature of the heart (motion-induced signal dropout, spatial shifts, beat-to-beat variation, and/or false ECG triggers) the data can be affected by physiological noise at the expense of SNR. The larger variance in SNR for a lower number of averages is expected based on fewer data available for averaging. The minimal variation between the MD and FA maps demonstrates that the specific DAS is not critical to estimating these properties. However, when using an oversampled number of diffusion directions (>6 directions), like DAS_15,4, a better apparent estimation of the HA is measured while averaging still benefits the overall SNR more so than more directions.

Conclusion

The outcome of this study showed that acquiring 12-20 directions for 5-3 averages provides robust tensor invariants and quality estimates of the helix angle while keeping scan times fixed to an acceptable duration. Further work is required to determine combinations of directions and averages to define the best cDTI acquisition protocol. Future work will use bootstrapping to estimate the cone of uncertainty in the primary eigenvector as an additional data quality metric.

Acknowledgements

We would like to acknowledge our funding sources which include NIH R01 HL131823 to DBE and NIH R01 HL152256 to DBE.