Synopsis

Keywords: Myocardium, Diffusion/other diffusion imaging techniques

Diffusion MRI in the brain has undergone tremendous advances in the last two decades while cardiac and general diffusion in the body show a lower speed. As for modelling, either isotropic or diffusion tensor imaging (DTI) are, by far, the methods used outside the brain. In this abstract we intend to quantify the better modeling capabilities of higher order (HO) methods than DTI, i.e., than Gaussian distributions. We show, by means of ex-vivo diffusion in pig hearts, that non-Gaussianity is observable and that diffusion weighted images (DWI) generated out of a HO model show more closeness to reality than DTI.

Purpose

Diffusion MRI (dMRI) is a clinical imaging modality based on the measurement of Brownian movement within body tissues. Although this technique has gone through tremendous advances in the brain, cardiac diffusion shows a much lower speed. Cardiomyocytes are the basic contractile elements in the heart. They have a highly organized microstructure consisting of helices ranging from the apex to the base, with angles that change according to the depth in the myocardium. This helical arrangement is assumed to be responsible for the rotation and torsion of the myocardium during ventricular contraction (see [Nielles‐Vallespin20] and references therein). However, this microstructure by itself does not suffice to explain other observed contractile effects, such as wall thickening. Therefore, the existence of a secondary structure consisting laminar elements (known sheetlets) has also been reported [Smerup09]. Cardiac diffusion is more complicated than the brain counterpart in terms of acquisition since bulk motion is several orders of magnitude greater than water molecules diffusion; hence, cardiac acquisition methods have to specifically address the issue of bulk motion so that diffusion is not hidden by this primary effect. The DTI model is by far the most used in cardiac diffusion for different applications [Nielles-Vallespin20] and, specifically, for scar characterization. Three examples of such applications are [Pashakhanloo17], [Mekkaoui18] as well as [León19]. The DTI model, however, is incapable of accounting for the sheetlet arrangement mentioned above. Very few attempts, to the best of our knowledge, have been described in the literature in moving beyond DTI, i.e. in accounting for diffusion patterns that moved beyond a Gaussian distribution. Actually, [Mekkaoui17] is reluctant with Diffusion Spectrum Imaging (DSI) approaches. In this abstract we compare the Gaussian diffusion model with a higher order model for EAP. We show that the diffusion pattern deviates substantially from the Gaussian assumption and diffusion weighted images created out of a more general EAP are closer to those observed for two ex-vivo pig hearts.

Methods

Datasets: DWIs used for this experiment were two different volumes (Volumes 1 and 2) of ex-vivo pigs hearts with the following multishell schemes (expressed as b values –in s/mm2 and number of gradients within braces): 300(8) ,600(16), 900(32), 1200(32), 2000(64), 3600(64). In order for calculations to be performed within myocardium points, a mask has been defined by an expert using in-house software.EAP modelling: A fully non-parametric, DSI-based representation of the EAP was used. In precise terms, we adapted the so-called Hybrid Diffusion Imaging DSI (HyDI-DSI) [Wu07] to a constrained version where the EAP is forced to have unit mass and its samples to be non-negative [Tristán-Vega22]. This way, a regular lattice of 9x9x9 of non-negative samples was arranged at each voxel so that the whole extent of the EAP (assessed from the DTI-estimated diffusion properties of the voxel) was properly sampled. From this lattice, the theory on Fourier analysis allows to recover the attenuation signal (the DWI channels over the baseline image) at any desired points.Working hypothesis: Let be the original signal acquired by the scanner for each wave-vector q. Let be signal that can be recovered from the diffusion tensor D. Let be the signal that can be recovered from the HyDI-DSI described above. Then:$$$E(q) = E_{DSI}(q) + \Delta_{DSI}E(q) + w(q)$$$$$$E(q) = E_{DTI}(q) + \Delta_{DTI}E(q) + w(q)$$$where $$$w(q)$$$ comprises the acquisition noise and other artifacts and $$$\Delta_{DTI}$$$, $$$\Delta_{DSI}$$$ are the residuals standing for the part of the diffusion signal that cannot be explained by either model (DTI or DSI). We hypothesize that most of the voxels will be significantly better fitted by the DSI model than they are by the DTI, i.e. $$$E\{\Delta^2_{DTI}\} - E\{\Delta^2_{DSI}\} >> 0$$$.Cross-validation: To estimate $$$E\{\Delta^2_{DTI}\} - E\{\Delta^2_{DSI}\}$$$, we use 10-fold cross-validation. For each of the 10 folds:We build a test set by randomly choosing three evenly spaced gradient directions at each shell.All the remaining gradient directions at all shells are used to fit both the HyDI-DSI model and a tensor model (using positive-definite constrained non-linear least squares).Assuming the residuals, the noise and the attenuation signal itself are uncorrelated, we estimate the difference between the fitting residuals as: $$E\{\Delta^2_{DTI}\} - E\{\Delta^2_{DSI}\} \simeq \overline{(E(q_{test})-E_{DTI}(q_{test}))^2} - \overline{(E(q_{test})-E_{DSI}(q_{test}))^2}$$ where we have used sample averages $$$\overline{x}$$$ to estimate the expected values. This estimate is computed or each of the six shells independently, since the Gaussian mismatch is expected to increase for the outermost shells.Finally, we define a “non-Gaussianity” index (NG) as the normalized value of the difference of residuals at each shell: $$NG = \frac{E\{\Delta^2_{DTI}\} - E\{\Delta^2_{DSI}\}}{\overline{E(q_{test})^2}}$$

Results

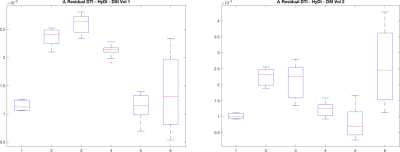
Figure 1 shows the NG maps for the two volumes in different short-axis slices. Figure 2 shows boxplots of the quantity defined in the third bullet of the cross validation procedure defined above. Averages have been computed within myocardium points, for each of the folds, where averages are computed on values within the mask. Six boxplots are computed, one per shell, by stacking values along the folds for each of the three gradient directions selected in each fold.

Conclusion

Non-Gaussian diffusion seems to take place in the heart. More involved modeling techniques for the EAP that the DTI model are a better match to reality. Clinical consequences are yet to be demonstrated, but this result opens a door for further insight.

Acknowledgements

The authors acknowledge grants PID2020-115339RB-I00, TED2021-130090B-I00 and PID2021-124407NB-I00 from the Ministerio de Ciencia e Innovación of Spain. The support from ESAOTE Ltd. is also acknowledged.

References

León, D. G., López-Yunta, M., Alfonso-Almazán, J. M., Marina-Breysse, M., Quintanilla, J. G., Sánchez-González, J., ... & Pérez-Villacastín, J. (2019). Three-dimensional cardiac fibre disorganization as a novel parameter for ventricular arrhythmia stratification after myocardial infarction. EP Europace, 21(5), 822-832. Mekkaoui, C., Reese, T. G., Jackowski, M. P., Bhat, H., & Sosnovik, D. E. (2017). Diffusion MRI in the heart. NMR in Biomedicine, 30(3), e3426.Mekkaoui, C., Jackowski, M. P., Kostis, W. J., Stoeck, C. T., Thiagalingam, A., Reese, T. G., ... & Sosnovik, D. E. (2018). Myocardial scar delineation using diffusion tensor magnetic resonance tractography. Journal of the American Heart Association, 7(3), e007834.Nielles‐Vallespin, S., Scott, A., Ferreira, P., Khalique, Z., Pennell, D., & Firmin, D. (2020). Cardiac Diffusion: Technique and Practical App. Journal of Magnetic Resonance Imaging, 52(2), 348-368.Pashakhanloo, F., Herzka, D. A., Mori, S., Zviman, M., Halperin, H., Gai, N., ... & McVeigh, E. R. (2017). Submillimeter diffusion tensor imaging and late gadolinium enhancement cardiovascular magnetic resonance of chronic myocardial infarction. Journal of Cardiovascular Magnetic Resonance, 19(1), 9.Smerup M, Nielsen E, Agger P, et al. The three-dimensional arrangement of the myocytes aggregated together within the mammalian ventricular myocardium. Anat Record 2009;292:1–11.Tristán-Vega A, Pieciak T, París G, Rodríguez-Galván JR, Aja-Fernández S. HYDI-DSI revisited: constrained non-parametric EAP imaging without q-space re-gridding. Medical Image Analysis 2022.Wu Y-C, Alexander AL. Hybrid diffusion imaging. NeuroIm 2007; 36(3):617–629.