Synopsis

Keywords: Magnets (B0), Screening, Passive shielding

Passive shielding is a feasible approach to constrain the strong magnetic fluxes in ultrahigh field MRI superconducting magnets. However, an in-depth investigation of the passive shielding design is not well discussed in the literature and notably lacks nonlinear optimization design/analysis methods for this practice. This work developed a computation algorithm for passive shielding design, which uses an integral operation with nonlinear iteration. An exemplification for shielding a 9.4T whole-body MRI superconducting magnet showed the significant advantages of the proposed method over commercial packages. The optimized passive shielding scheme will be used in our future magnet engineering projects.

Introduction

Although it is very attractive to use active shielding on magnetic resonance imaging (MRI) superconducting magnets due to the magnetic field stability, magnet mobility, infrastructure construction, etc., passive shielding is still a good choice when the magnetic field strength is close to the superconducting limit, such as ultra-high field MRI [1]. Nearly all the existing 9.4T whole-body MRI superconducting magnets are passively shielded, which is also true for the 10.5T MRI superconducting magnet at the University of Minnesota [2]. The Iseult 11.75T MRI superconducting magnet applied a bold scheme of active shielding after carefully evaluating the stray field extent and the integral project cost [3]. To operate these superconducting systems safely, the 10.5T magnet runs at 3.0K to elevate the current margin, typically at the 4.2K liquid helium temperature of those 9.4T ones. The 11.75T magnet uses the dilution cooler to reduce the temperature further to 1.8K. Active shielding at the ultrahigh field will significantly increase the cryogenic volume and superconducting wire usage, and add risks to the critical performance and stress of magnet coils. Therefore, studying passive shielding for ultrahigh MRI is essential for future development.

Methods

An integral method was developed for the magnetization computation of ferromagnetic materials, and an iterative algorithm was proposed for the nonlinear solution convergence. With the Gauss theorem, the classical magnetization equation is expressed as Eq. (1) [4].$$\phi=-\frac{1}{4\pi}\int_{S'}\frac{\triangledown\phi\cdot{dS'}}{|r-r'|}+\frac{1}{4\pi}\int_{V'}\frac{div(\triangledown\phi)}{|r-r'|}dV'$$where φ is the scalar potential, S' is the integral surface, r is the observation point, r' is the source point, div is the divergence operation, and V' is the integral volume.
Here the singularity problem can be avoided by targeting the observation point at the barycenter of the tetrahedral element. A nonlinear relationship between the magnetic field and the magnetization makes it troublesome to seek the solution by matrix inversion. We applied an iterative operation to address the nonlinear calculation problem, and the core algorithms are expressed in Eq. (2).$${\bf H}=-\triangledown{\bf \phi}\scriptsize i$$$${\bf M}=f({\bf H})$$$${\bf \chi}=\bf M/H$$$${\bf Z=A\chi}-eye(n)$$$${\bf \phi}{\scriptsize i+1}={\bf \phi}{\scriptsize i}/2-{\bf Z^{-1}\phi}{\scriptsize 0}/2$$$$e=\sum({\bf Z\phi}{\scriptsize i+1}+{\bf \phi}{\scriptsize 0})^2$$where H is the magnetic field intensity, M is the magnetization intensity, f() indicates the nonlinear function relationship between H and M, χ is the relative permeability, A is the transform matrix calculated by Eq. (1), eye(n) is a unit matrix, Z is the coefficient matrix of φ, φ₀ is the source scalar potential, i is the iterative quantity, and e is the iterative error used to estimate the convergence process.
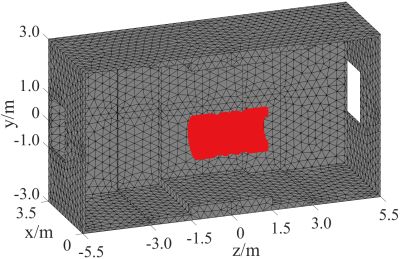
A passive shielding exemplification was proposed for a designed 9.4T whole-body MRI superconducting magnet. The iron shield house dimension with integral elements is illustrated in Fig. l. The engineering construction of the passive shielding structure and complete 9.4T MRI system integration is under preparation [5].

Results

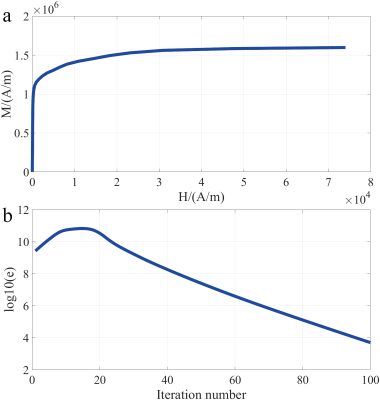
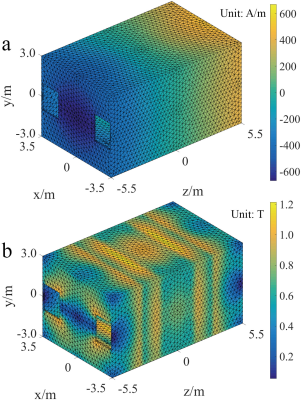
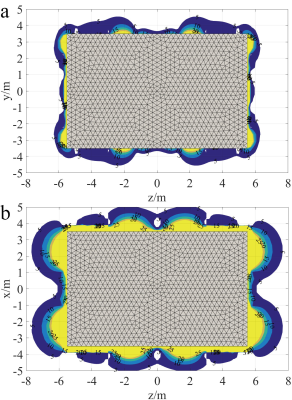
The M-H relationship and iterative step for the nonlinear computation are displayed in Fig. 2 for comparison. After about 100-step iterations, the error was reduced by more than 6 orders, and a sufficiently accurate solution was achieved. The scalar potential distribution of the iron shield house is shown in Fig. 3(a), where it generally presents positive and negative sections at the two halves of the longitudinal direction. An illustration of the magnetic flux density in Fig. 3(b) can help make an intuitive understanding of the magnetization effect. Since a strong stray field is near the magnet, a corresponding thick iron arrangement at the central part augments the ability to limit stray field leakage. A spare material layout with thin iron at the axial ends can realize a good shielding effect. The stray field contours are illustrated in Fig. 4, where Fig. 4(a) is the stray field distribution at the front-view cross-section, and Fig. 4(b) is the stray field distribution at the top-view cross-section. They show that the 5Gauss lines are restricted close to the iron shield profile.

Discussion

The proposed passive shielding algorithm has unique advantages compared with commercial packages such as ANSYS, Comsol, etc. Since there is no need to mesh the air space in the proposed method, the computation load is much smaller, and the operation is much more flexible than the finite element method. Most importantly, the integral operation makes it possible to calculate the magnetic flux in entities which have very adjacent interval or entities with very complex structures. By contrast, the finite element method can meet challenges in tackling these situations due to element meshing problems.

Conclusion

An integral operation with nonlinear iteration was proposed in this work to design passive shielding structure with arbitrary geometry for ultrahigh field MRI superconducting magnets. The algorithm is efficient, flexible, and powerful to cope with complex computation tasks. A 9.4T passively-shielded whole-body MRI superconducting magnet was designed based on the proposed method, which showed a very compact 5Gauss line restriction. The passive shielding technique will be further developed to support further future ultrahigh field MRI system development.

Acknowledgements

This work is funded by the National Science Foundation of China (Grant No.52277031), the International Partnership Program of Chinese Academy of Sciences (Grant No. 182111KYSB20210014), the Beijing New-star Plan of Science and Technology (Grant No. Z211100002121134), the Magnetic Resonance Union of Chinese Academy of Sciences (Grant No. 2021gzl002), the National Key Research and Development Program of China (Grant No. 2020YFF01014702) and the Chinese Academy of Sciences Pioneer Hundred Talents Program (Grant No. Y8402A1C31).