Synopsis

Keywords: High-Field MRI, MR Fingerprinting, Quantitative Imaging, Tissue Characterization, Brain

MR fingerprinting enables for robust simultaneous quantitative parametric mapping and is usually performed with spiral acquisitions. These are particularly sensitive to B₁ inhomogeneities and hence more susceptible at ultra high-field. To mitigate B₁ inhomogeneity effects, we implemented a Cartesian MRF approach. Cartesian 2D data collection time is somewhat slow, and we overcome this by demonstrating the feasibility of GRAPPA acceleration for applications in phantoms and in vivo. We present a fully sampled Cartesian data set in a phantom and in vivo, and we present the performance of increasing GRAPPA acceleration factors to reduce scan time significantly, without compromising image quality.

Introduction

Magnetic resonance fingerprinting (MRF) [1] enables for robust simultaneous quantitative multi-parametric mapping in a single acquisition. It is usually performed with spiral acquisitions [2]. These are particularly sensitive to B₀ inhomogeneities and hence more susceptible at ultra high-field. As an alternative due to its inherent robustness to mitigate B₀ inhomogeneity effects, we implemented an MRF approach based on interleaved Cartesian k-space sampling for rapid assessment of T₁, T₂, B₁⁺ and proton density at ultra-high field. Cartesian 2D data collection time is somewhat slow which may limit the applications of this imaging strategy. We overcome this by demonstrating the feasibility of GRAPPA [3] acceleration for applications at 7T. We present a reference dataset comprising fully sampled Cartesian MR Fingerprinting data from a phantom, and we present the effectiveness and performance of increasing GRAPPA acceleration factors in both phantom and in vivo to reduce scan time significantly, without compromising image quality.

Methods

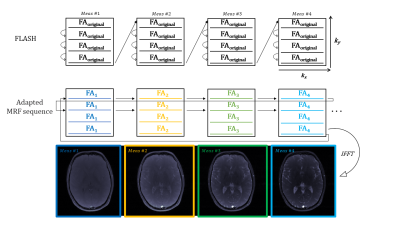
All experiments were performed on a MAGNETOM Terra 7T scanner (Siemens Healthineers, Germany). An agar phantom [6] was scanned in a mid transverse slice to acquire test data using a 8Tx32Rx head coil (Nova Medical Inc). Our interleaved Cartesian MRF sequence is based on FLASH with variable flip-angles (FA) and fixed repetition times (TR) as shown in Figure 1. We applied a FOV of 200mm, slice-thickness of 5mm, matrix size of 128x128mm and 512 measurements. With our sequence design we acquired a fully sampled Cartesian MRF dataset, which is reconstructed online with 2D Fourier transformation in phantoms and in vivo. We then ran a series of acquisitions with different GRAPPA factors to investigate the effect of prospective undersampling.

This Cartesian MRF approach was matched against an Extended Phase Graph (EPG) dictionary simulation to make quantitative parameter maps in a voxel-by-voxel basis. The MRF framework pipeline includes dictionary generation based on extended phase graph [5] formalism. The vector-dot product matching and quantitative map generation was implemented from scratch in MATLAB (Mathworks,2021b). In addition to the main parameters, B₁ from Bloch-Siegert measurement was simulated as an additional dimension of the dictionary, with a range between 0.1 and 2.5 in steps of 0.1. The actual FAs were calculated as nominal FAs multiplied by B₁. For each B₁ value, a total of 401548 signal time courses, each with 512 time points, were simulated for a range of possible T₁ values (10 to 1000ms in steps of 10ms, 1000 to 2000ms in steps of 20ms, and 2000 to 3000ms in steps of 100ms), T₂ values (10 to 100ms in steps of 20ms, and 2000 to 3000ms in steps of 20ms).

Results

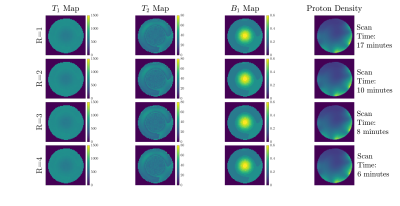
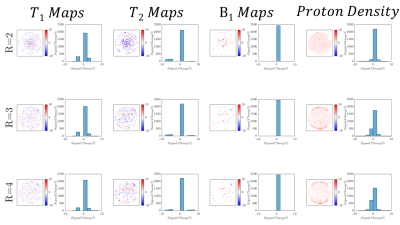
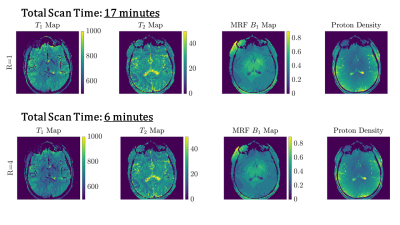
Figure 1 shows a schematic representation of the original FLASH sequence and changes in line acquisition direction that were made for our adapted Cartesian MRF sequence, showing the raw k-space data acquisition per measurement for our pattern of flip angles for 512 measurements. An image is then reconstructed through Fourier transform from the same block of RF pulses.
Figure 2 demonstrates a fully sampled Cartesian MRF dataset (R=1) with B₁ correction, acquired in a spherical phantom. We computed corresponding T₁ map, T₂ map, B₁⁺ map and proton density maps from the same slice. Each row presents a GRAPPA acceleration factor (R=2,R=3,R=4). Figure 3 shows difference in signal within the same slice compared to R=1, calculated in percentage, for T₁ maps, T₂ maps, B₁⁺ maps and Proton Density maps for GRAPPA acceleration (R=2,R=3,R=4). Histograms reveal the differences in the relative mean signal. Figure 4 displays a fully sampled (R=1) MRF dataset in the brain, with corresponding quantitative maps (T₁ maps, T₂ maps, B₁⁺ maps, Proton Density Maps), resulting in a total scan time of approximately 17 minutes. We demonstrate an MRF dataset in the brain with an accelerating factor (R=4) in the brain, with corresponding quantitative maps, resulting in a total scan time of 6 minutes, reducing the total scan time to one fourth.

Discussion

We have acquired a fully-sampled interleaved Cartesian k-space dataset with an MRF flip angle and repetition time train in phantoms and in vivo. This matches a dictionary computed with the extended phase graph formalism. We have prospectively under sampled phantom data sets to understand the impact of the acceleration factors using GRAPPA to showcase accelerated MRF sampling in phantom data and in vivo. We have successfully reduced the scan time by half without compromising image quality of the outcoming parametric maps. Our future work will focus on accelerating our pulse sequence approach even further, to understand the ultimate limit of GRAPPA accelerated MRF. So far we have used integrated reference lines but in future work we will acquire the GRAPPA reference in a separate pre-scan for faster accelerated MRF.

Conclusion

We demonstrate a new approach for accelerating 2D Cartesian MRF acquisition and reconstruction using GRAPPA. With this strategy, comparable parametric maps can be acquired with a notably reduced scan time. The effective scan time for R=4 for brain MRF is around 7 minutes.

Acknowledgements

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 801075. CTR was funded by a Sir Henry Dale Fellowship from the Wellcome Trust and the Royal Society [098436/Z/12/B]. This study was supported by the NIHR Cambridge Biomedical Research Centre and MRC Clinical Research Infrastructure Award for 7T. This work was supported by Innovate UK [10032205] under the Guarantee Scheme relating to the EU Horizon Europe project MITI [101058229].