Synopsis

Keywords: Electromagnetic Tissue Properties, Quantitative Susceptibility mapping, Multi-echo, ROMEO, Phase

With increasingly popular multi-echo QSM, the combination of echoes becomes important in terms of accuracy, SNR and computation time. We compared 6 different pipelines with quantitative and Laplacian unwrapping and three different echo combination approaches, weighted averaging of QSMs, combination of the phase, and non-linear fitting. We compared the pipelines on the QSM challenge brain dataset and 7 T in vivo data and conclude that quantitative unwrapping (ROMEO) with weighted frequency combination achieves the best outcomes in terms of accuracy, SNR and computation time.

Introduction

To successfully integrate Quantitative Susceptibility Mapping (QSM) into clinical practice, the QSM algorithm must not only be accurate but also fast. This is even more challenging with multi-echo acquisitions becoming more popular for QSM. Different ways of combining the echo information include non-linear fitting [1], frequency or phase averaging [2, 3], and also averaging of the final QSMs [4]. A range of Laplacian based methods for combining echo data before dipole inversion were investigated previously [5], but using a quantitative unwrapping procedure instead could have significant benefits over Laplacian methods [6]. Here, we investigate how a quantitatively unwrapped multi-echo phase combination performs for combining multi-echo data for QSM processing.

Methods

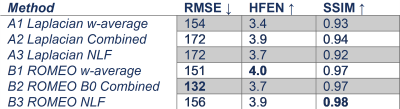
To test our hypothesis, two different datasets were used, the in silico head phantom with 1 mm isotropic resolution from the QSM challenge 2019 [7] and an in vivo data set acquired at 7 T with 8 echoes, where coil-combination and phase offset removal were performed using ASPIRE [8]. We compared three different echo combination approaches, 1) weighted-average of the final QSMs, 2) weighted combination of unwrapped phase, and 3) non-linear fitting (NLF) using MEDI [1]. All approaches are performed with 2 different unwrapping choices, A) Laplacian unwrapping, and B) the quantitative unwrapping method ROMEO [9], giving a total of 6 different pipelines. For the applications of weighted averaging in 1) and 2), inverse-variance-weighted echo-combination was applied to combine phase and QSM respectively [2, 3]. The QSM processing was identical for all 6 pipelines with the same mask, which was obtained by thresholding the phase quality map from the quantitative unwrapping procedure ROMEO. The background field correction VSHARP and the Dipole inversion RTS [10] were performed using QSM.jl [https://github.com/kamesy/QSM.jl]. The quantitative results were calculated inside the mask using the root mean squared error (RMSE), high frequency error norm (HFEN), and structural similarity index metric (SSIM).

Results

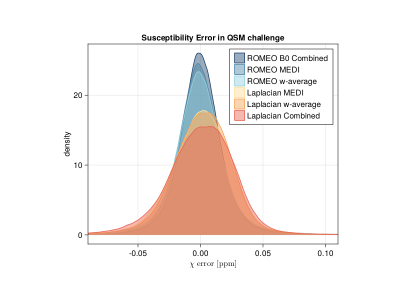
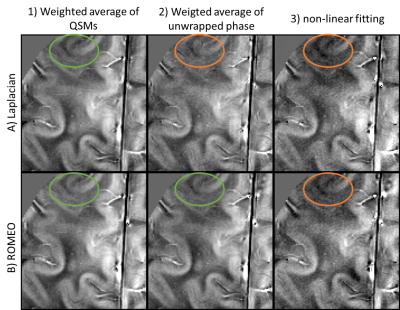
The ROMEO pipelines were more accurate than the Laplacian pipelines on the QSM challenge data (Figure 1). With in vivo data, the visual appearance was similar with all 6 pipelines in regions of high phase SNR (not shown), but Laplacian – Combined Phase and both NLF pipelines were adversely affected by higher noise in regions of lower phase SNR (Figure 2). In the evaluation of image metrics (Table 1), RMSE shows a similar result, with the ROMEO B0 approach having the lowest value and both NLF and Laplacian – Combined Phase having higher RMSE values. For SSIM, all three ROMEO approaches had higher values than the Laplacian approaches. For HFEN, there is no clear tendency.

Discussion and Conclusion

The Combined Phase approaches (A2, B2) were approximately 8 to 10 times faster for the 8 echo in-vivo dataset. This is because background field removal and dipole inversion are usually the most time-consuming steps, and both are only performed once in the Combined Phase approaches. Non-linear fitting (A3, B3) was similarly expensive as QSM processing, increasing the computation time by about a factor of 2 compared to the Combined Phase approaches, but it was faster than averaging QSMs. The visual comparison showed the reduced SNR in non-linear fitting (A3 and B3) compared to averaging the QSMs and the phase (A1, B1 and B2), which is agreement with Chen et al. [11]. The weighted averaging of Laplacian unwrapped phase also led to lower SNR (A2). The ROMEO B0 approach (B2) was computationally efficient, had high SNR and the lowest RMSE metric and its the reduced runtime might benefit translation into clinical workflows.

Acknowledgements

No acknowledgement found.