4182
Pseudo COSMOS: Efficient deep learning quantitative susceptibility mapping based on local field transformation1Department of Computer Science and Information Engineering, National Cheng Kung University, Tainan, Taiwan, 2Graduate Institute of Biomedical Electronics and Bioinformatics, National Taiwan University, Taipei, Taiwan, 3Institute of Medical Informatics, National Cheng Kung University, Tainan, Taiwan
Synopsis
Keywords: Susceptibility, Machine Learning/Artificial Intelligence
A deep learning framework termed pCOSMOS for quantitative susceptibility mapping (QSM) was proposed, which employed a local-field-to-local-field transformation to generate multiple orientation local field maps from single orientation data, followed by COSMOS reconstruction using physical model. 3T multi-orientation data from 10 healthy subjects (7 for training, 3 for testing) were used to investigate performance. Quantitative results compared with MEDI, SFCR, QSMnet, and LPCNN demonstrated superior performance of pCOSMOS comparable to the amongst best algorithms using single orientation data, while showing drastically reduced training time from tens of hours to 3.2 hours.Introduction
Deep learning approaches with convolutional neural network (CNN) have recently gained increasing popularity in quantitative susceptibility mapping (QSM) to solve the ill-posed dipole inversion problem with single-orientation data 1. Lessons learned from the QSM 2.0 Challenge suggest that deep learning with addition of forward model to update its weights in the QSM prediction stage tend to perform superiorly via an improvement in physical properties of the method and fidelity 1,2. The incorporation of physical model to update weights, however, causes substantial lengthening in network training time. To solve this issue, therefore, we propose a method that reserves the CNN for local-field-to-local-field transformation generating multi-orientation data from single-orientation local field maps, thereby shifting the physical modeling task to physical reconstruction using calculation of susceptibility through multiple orientation sampling (COSMOS) 3. We term this method pseudo COSMOS or pCOSMOS, and demonstrate its training acceleration at the same time with preserved tissue boundary details.Methods
Ten healthy volunteers (mean age 27.8; 7 used for training and 3 for testing) were scanned at 3T using 3D gradient echo (GRE) sequence with isotropic voxel size 1×1×1 mm3, five orientations (five different orientations including normal position, tilted forward, tilted backward, tilted right and tilted left), TR = 45 ms, bandwidth (BW) = 31.25 KHz, TE1/δTE = 6/6 ms, six echoes, flip angle = 15°, eight-channel head coil, field of view (FOV) = 224×224×150~170 mm3 padded with zeros to 224×224×224 mm3. Preprocessing consisted of brain extraction, phase unwrapping, and background field removal. The susceptibility maps derived using COSMOS with the five acquired datasets were treated as reference standard.The proposed pCOSMOS framework used 3D U-net (Fig.1) with single-orientation local field maps as input (axial orientation), with 5 outputs for local field maps at fixed predefined orientations at 60 degrees apart for optimal noise suppression 3. These outputs were then fed to COSMOS to obtain the final susceptibility maps. Generation of labels for local field maps at the five predefined angles were created from forward dipole convolution with the COSMOS susceptibility maps. Loss function consisted of L1 loss and gradient loss 4. Linear scaling was applied to the predicted results according to the standard deviations of the histograms to yield identical distribution to the labeling data. The deep learning model was implemented with Python and Pytorch 1.8.0 on Intel Core i7-9700K CPU, Geforce RTX 2080 Ti GPU, with 64GB RAM. Adam optimizer was used with learning rate = 0.0001, batch size of 4, and 400 training epochs. For comparison, results from MEDI 5, SFCR 6, QSMnet 4, and LPCNN 7 were also shown.Results
Susceptibility maps estimated using pCOSMOS seemed to yield less streaking artifacts than COSMOS and MEDI, better preserve gray-white matter boundary details than QSMnet and LPCNN (Fig.2), and exhibited less errors than MEDI and SFCR (Fig.3). Region-of-interest analysis on substantia nigra, red nucleus, globus pallidus, putamen, and caudate nucleus also indicated that pCOSMOS as well as QSMnet gave susceptibility values in better consistency with those from COSMOS then the other three methods (Fig.4). Linear regression analysis suggested that pCOSMOS results were slightly inferior to LPCNN but comparably better than the other three methods (Fig.5). Total training time with seven training subjects was 3.2 hours for pCOSMOS, 12 hours for QSMnet, and 2 days for LPCNN, respectively.Discussion
Training of current CNN is in general efficient when dealing with qualitative pictures. The proposed pCOSMOS framework establishes a local-field-to-local-field transformation similar to picture management, thus bypassing the need for the time-consuming task of tuning network weights using physical models. The need for only single-orientation data makes pCOSMOS suitable for clinical applications where scan time tolerance becomes a critical issue. It is noted that for application purpose, lengthy training time is relatively unimportant, as prediction is often very fast after model maturation. The advantage of rapid training in pCOSMOS is therefore beneficial during the technical development stage, where various combinations of modeling need to be tested for precision, accuracy, and effectiveness. It is therefore concluded that the propose pCOSMOS scheme may find usefulness for subsequent developments of QSM using deep learning.Acknowledgements
No acknowledgement found.References
1. QSM Challenge 2.0 Organization Committee, Bilgic B, Langkammer C, Marques JP, Meineke J, Milovic C, Schweser F. QSM reconstruction challenge 2.0: Design and report of results. Magn Reson Med 2021;86(3):1241-1255.
2. Zhang J, Liu Z, Zhang S, Zhang H, Spincemaille P, Nguyen TD, Sabuncu MR, Wang Y. Fidelity imposed network edit (FINE) for solving ill-posed image reconstruction. Neuroimage 2020;211:116579.
3. Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med 2009;61(1):196-204.
4. Yoon J, Gong E, Chatnuntawech I, Bilgic B, Lee J, Jung W, Ko J, Jung H, Setsompop K, Zaharchuk G, Kim EY, Pauly J, Lee J. Quantitative susceptibility mapping using deep neural network: QSMnet. Neuroimage. 2018 Oct 1;179:199-206.
5. Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, Wang Y. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison with COSMOS in human brain imaging. Magn Reson Med 2011;66(3):777-83.
6. Bao L, Li X, Cai C, Chen Z, van Zijl PC. Quantitative Susceptibility Mapping Using Structural Feature Based Collaborative Reconstruction (SFCR) in the Human Brain. IEEE Trans Med Imaging. 2016 Sep;35(9):2040-50.
7. Lai KW, Aggarwal M, van Zijl P, Li X, Sulam J. Learned Proximal Networks for Quantitative Susceptibility Mapping. Med Image Comput Comput Assist Interv. 2020 Oct;12262:125-135.
Figures
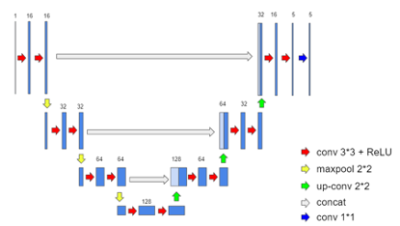
Fig.1
The network structure of a 4-layer 3D U-net used in pCOSMOS, consisting of 15 convolution layers, 14 batch normalization, 14 ReLU, three max-pooling, three transposed convolution layers, and three skip connections, with patch training at the size of 64x64x64.
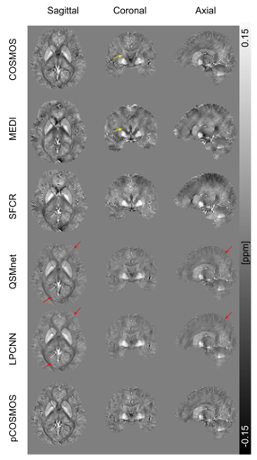
Fig.2
Example of QSM-reconstructed susceptibility maps by five methods using single orientation data displayed with COSMOS treated as ground truth. Yellow arrows indicate the streaking artifacts on the subject. Red arrows indicate brain gray matter folds with unclear boundaries.
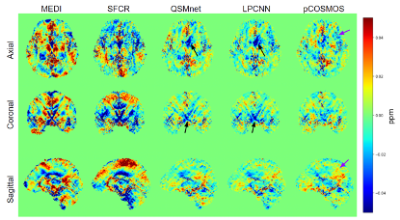
Fig.3
Residual error maps for each method. Black arrows indicate regions with more errors clustered. Purple arrows indicate regions with scattered errors.
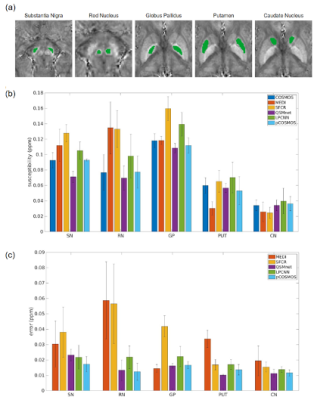
Fig.4
Regions-of-interest (a) selected from substantia nigra, red nucleus, globus pallidus, putamen, and caudate nucleus, from which the susceptibility values were measured using the five single-orientation methods with COSMOS (b). And (c) shows voxel-wise errors of the five methods.
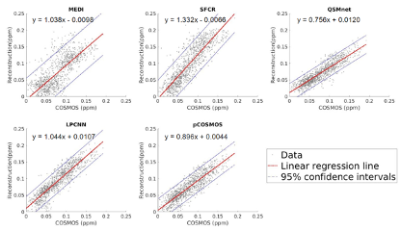
Fig.5
Linearity test comparing susceptibility values measured using the five single-orientation methods versus COSMOS, showing the linear regression lines and 95% confidence intervals.