4171

Deep Fourier-Space Inversion
Mathias Lambert1,2,3, Javier Silva1,2,3, Carlos Milovic4, and Cristian Tejos1,2,3
1Department of Electrical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 2Biomedical Imaging Center, Pontificia Universidad Católica de Chile, Santiago, Chile, 3Millennium Institute for Intelligent Healthcare Engineering (iHEALTH), Santiago, Chile, 4School of Electrical Engineering, Pontificia Universidad Católica de Valpaiso, Valparaiso, Chile

Synopsis

Keywords: Susceptibility, Quantitative Susceptibility mapping

Guiding the network architecture to learn to apply the kernel inversely in Fourier space allows training to be less prone to overfitting. Using simulated images from a single brain image, it is possible to satisfactorily reconstruct a susceptibility map of the abdomen. By having as input the Fourier space of the local field and the kernel of the dipole, the network learned to reduce the noise, to divide the data of the local field by the kernel where possible and to recover the data in the magic cone.


Introduction

QSM is an ill-posed inverse problem that is commonly solved by optimization techniques that require parameter tuning. Deep learning-based solutions1 have emerged to solve this problem and speed up the process. However, training these models is complex as they must learn the underlying model (a deconvolution with the dipole kernel) and denoising. Usually, in vivo data (solutions provided by iterative methods or solutions obtained by COSMOS2 ) or synthetic data generated from the forward model are used to train these models. We present Deep Fourier-Space Inversion, which is a Deep Learning-based model that solves QSM using as input the Fourier space of the local field and the dipole kernel. In this way, instead of learning how to transform the local field into the susceptibility distribution by operations in the image domain, the proposed model learns how to inversely apply the supplied dipole kernel, filtering out the noise and filling values in non-defined areas (i.e., in the magic cone).

Methods

Deep Fourier-Space Inversion
Deep Fourier-Space Inversion is a 3D U-net (Figure 1) that receives a three-channel tensor as input. The first and second channels encode respectively the real and imaginary part of the Fourier Transform of the local field. The third channel encodes the dipole kernel in the Fourier domain. In this way the model performs the inverse operation with a priori knowledge of the kernel.

We tested the capability of the proposed model in two experiments with two different training techniques:


  1. Training with simulated data from a single brain image: From a resized version (128x128x128) of the ground truth from simulation 1 of challenge 2.03. The model was trained using forward simulations from this data. Complex noise with SNR $$$\in$$$ [30, 300], dimension permutation, scaling of susceptibility values and isotropic dipole kernels with voxel size $$$\in$$$ [1, 3] mm3 were used. An abdominal phantom4 of QSM was used as a test.
  2. Training with simulated data from geometric figures: From 30,000 (64x64x64) images composed of random cylinders and spheres. Local field was forward simulated by dipole convolution, and complex gaussian noise (SNR:30-120) added to the simulated signal. The model was trained for 15000 steps. Additionally, a fine-tuning process with the following requirements was performed out to boost performance on larger images: From 2 synthetic T1 brain images5, we map the values to make the image and the distribution similar to that of a QSM map. Local field was forward simulated by dipole convolution with the following augmentations; dimension permutation, random weighting of paramagnetic and diamagnetic contributions, invert the susceptibility values, and complex gaussian noise (SNR:30-50 (30%) and 90-150 (70%)) added to the simulated signal. The simulations of the QSM challenge 2.0, an abdominal phantom of QSM, three forward simulations from COSMOS6 with SNRs 40, 100 and 100, the last one with a strong phase consistency of $$$\pm \pi$$$ were used as a test.
Both experiments used Adam as the optimiser, MSE as the loss function and were run on an RTX3090.
In both experiments, the performance of the proposed model was compared with QSMnet+7.

Results and Discussions​

Figure 2 presents the results of the training with simulated data from a single brain image experiment. Deep Fourier-Space Inversion obtains better NRMSE. This shows that the network is able to learn to invert the supplied kernel and is not learning the structure of the input image.
In the experiment training with simulated data from geometric figures (Figure 3), Deep Fourier-Space Inversion achieves better results on all data sets. It is observed that it manages noise and phase inconsistencies better. However, its reconstructions have a smoother appearance, possibly due to the use of MSE as a loss function.

Conclusions

Deep Fourier-Space Inversion demonstrates that it is possible to correctly train a network using few data. The use of operations in Fourier space gives us the advantage of avoiding over-fitting. Future work that could enhance the network is to choose a more appropriate loss function and include more elaborate forward simulations similar to those used in the QSM Challenge 2.0.

Acknowledgements

Grant funding: Fondecyt 1191710, Anillo ACT912064, Millennium Institute for Intelligent Healthcare Engineering, iHEALTH (ICN2021_004).

References

  1. Jung W, Bollmann S, Lee J. Overview of quantitative susceptibility mapping using deep learning: Current status, challenges and opportunities. NMR Biomed. 2022 Apr;35(4):e4292.
  2. Liu T, Spincemaille P, De Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med. 2009; 61: 196- 204.
  3. QSM Challenge 2.0 Organization Committee, Bilgic, B, Langkammer, C, Marques, JP, Meineke, J, Milovic, C, Schweser, F. QSM reconstruction challenge 2.0: Design and report of results. Magn Reson Med. 2021; 86: 1241- 1255.
  4. Silva J, Milovic C, Lambert M, Montalba C, Arrieta C, Uribe S, Tejos C. Realistic in silico abdominalQSM phantom. In:Proc.Intl. Soc. Mag. Reson. Med, 2022;p1985.
  5. Pinaya, Tudosiu, P.-D., Dafflon, J., da Costa, P. F., Fernandez, V., Nachev, P., Ourselin, S., & Cardoso, M. J. Brain Imaging Generation with Latent Diffusion Models. arXiv:2209.07162, 2022.
  6. Milovic C, Tejos C, Acosta-Cabronero J, Özbay PS, Schwesser F, Marques JP, Irarrazaval P, Bilgic B, Langkammer C. The 2016 QSM Challenge: Lessons learned and considerations for a future challenge design. Magn Reson Med. 2020 Sep;84(3):1624-1637.
  7. W. Jung, J. Yoon, S. Ji, J. Choi, J. Kim, Y. Nam, E. Kim, J. Lee. Exploring linearity of deep neural network trained QSM: QSMnet+. Neuroimage. 2020 May; 116619.

Figures

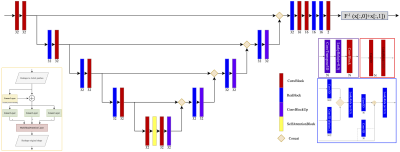
Figure 1: Network architecture. A transformer approach is used at the bottom of the Unet. All layers have LeakyRelu activation with slope=0.3.

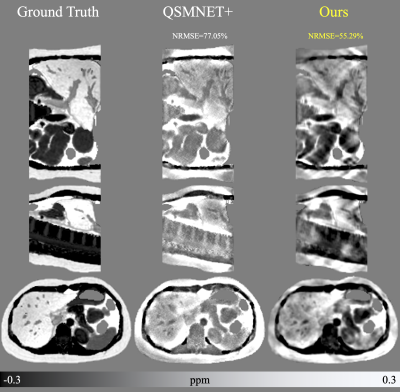
Figure 2: Results of the first experiments. The results show the ability of the network to reconstruct an abdomen data being trained with only one brain data.

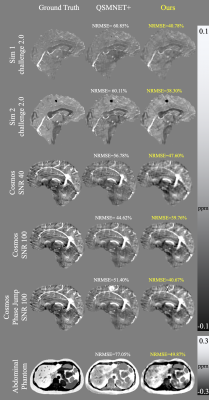
Figure 3: Results of the second experiment. Deep Fourier-Space Inversion obtained better NRMSE in all cases, along with a better ability to deal with noise and phase inconsistencies. However, its reconstructions have a smoothed appearance.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
4171
DOI: https://doi.org/10.58530/2023/4171