4165
Tractography of the subcortical U-fibers using a position-dependent maximum angle1ICTEAM, UCLouvain, Louvain-la-Neuve, Belgium, 2IoNS, UCLouvain, Louvain-la-Neuve, Belgium
Synopsis
Keywords: Brain Connectivity, Tractography & Fibre Modelling
Short association fibers in the subcortical white matter, also known as U-fibers, represent the connections between neighboring gyri. Due to the geometry of the cortical folds and the sharp turns along the cortical surface, tractography of U-fibers remains a challenge since increasing the maximum angle between tractography steps also increases the occurence of false positive streamlines. We propose to replace the fixed maximum angle value in tractography algorithms by an angular map, allowing higher angles at the interface between grey and white matter. This enables a more accurate tracking of U-fibers, while keeping a low number of false positive streamlines.Introduction
Subcortical U-fibers are short association fibers in the outer parts of the subcortical white matter representing connections between neighboring cortical areas. U-fibers are thought to be involved in multiple neurological and psychiatric diseases, such as in multiple sclerosis1 and Alzheimer’s disease2. Tracking U-fibers is more challenging compared to main white matter tracts due to the geometry of the cortical folds, requiring sharp turns to cover the cortical surface3. Obtaining U-fibers in a whole-brain tractogram requires a higher maximum angle between tractography steps to follow subcortical fibers along the cortical folds. However, a higher maximum angle increases the probability of generating false positive streamlines, increasing the post-processing steps required to clean the obtained tracts.We propose to replace the fixed maximum angle value in tractography algorithms by an angular map, which allows different values of maximum angle between tractography steps depending on the position in the brain. Allowing a higher angle at the interface between grey and white matter, with lower values in deep white matter, enables a more accurate tracking of subcortical U-fibers in whole-brain tractograms, while keeping a low number of false positive streamlines.
Methods
Modified tractography algorithmWe adapted the probabilistic tractography algorithm from DIPY4 to allow arrays in addition to single scalar values as input parameter for the maximum angle variable $$$\alpha_{max}$$$. The maximum angle variable becomes an angular map (Fig.1A) dependent on the position $$$(x, y, z)$$$ of the tractography step$$\alpha_{max}\rightarrow\alpha_{max}(x,y,z),$$which impacts the adjacency matrix $$$M_\textit{adj}\in\{0,1\}^{d\times d}$$$ used to compute the allowed directions from the current direction$$$\:\hat{d}$$$. The probability mass function $$$\textit{pmf}\:$$$bounded by $$$\alpha_{max}$$$ is obtained by$$\textit{pmf}_\textit{lim}=\textit{pmf}(x,y,z)*M_\textit{adj}(\alpha_\textit{max}(x,y,z),\hat{d}).$$The new direction is then selected amongst the direction which have a $$$\textit{pmf}_\textit{lim}>0\:$$$in a classic probabilistic tractography approach.
Data
Firstly, an in-vivo dMRI scan of a healthy adult participant was performed on a 3T GE SIGNA Premier scanner with the following parameters: 2mm isotropic voxels, 64 gradients at b=1000, 32 at b =2000,3000,5000s/mm2. Preprocessing included thermal denoising5, Gibbs ringing correction6, eddy-current distortion and movement correction7. A 3D T1 image (156 slices, 1mm isotropic, FOV:256x256mm2) was also acquired. Three regions of interests (ROIs) were placed in the hand motor cortex, somatosensory cortex and in the middle frontal gyrus to isolate U-fibers between adjacent gyri. The right middle frontal gyrus is responsible for numeracy8, which is linked to hand motor function9. Registration to the Desikan-Killiany atlas10 was accomplished using FreeSurfer. The frontoparietal part of the arcuate fasciculus (AF) was extracted from the whole-brain tractography using White Matter Query Language11.
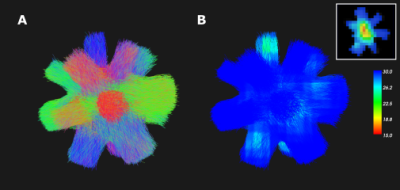
Secondly, a synthetic phantom from the Diffusion-Simulated Connectivity (DiSCo) dataset12 (Fig.2A) was used to compare the connectivity measures of 16 regions to a known ground truth. The dMRI protocol was composed of 360 gradients, spread over 4 b-value shells (b=1000,1925,3094,13191s/mm2). The DiSCo1 phantom was selected in the 2x2x2mm resolution.
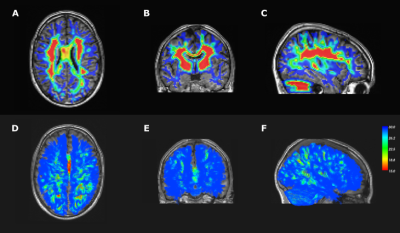
The local modeling of the in-vivo and synthetic data was performed with multi-shell multi-tissue spherical deconvolution (msmt-CSD)13. The modified probabilistic tractography described above was tested with an angular map based on the white matter fiber orientation distribution (FOD) obtained with msmt-CSD with $$$15°<\alpha_{max}<30°$$$ (Fig.1: in-vivo; Fig.2 synthetic data). The results were compared to the default probabilistic algorithm with $$$\alpha_{max}=15°$$$ and $$$\alpha_{max}=30°$$$.
The tractograms obtained from the synthetic data were filtered with SIFT14 and the connectivity matrices between the 16 ROIs were computed.
Results & Discussion
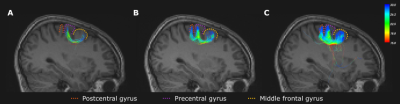
U-fibersThe streamlines linking the motor cortex to the adjacent gyri isolated from the tractogram in Fig.1F are displayed in Fig.3. The maximum angle of 15° (Fig.3A) is too low to tract the subcortical connections between the hand motor and somatosensory cortex due to geometry of the cortical fold. A maximum angle of 30° (Fig.3C) finds a large number of connections between both regions but also produces several false positive streamlines in deep white matter regions. The varying angle ranging from 15° to 30° produces no such streamlines while connecting both gyri to the motor cortex, without the need of exclusion zones or further post-processing.
White matter tracts
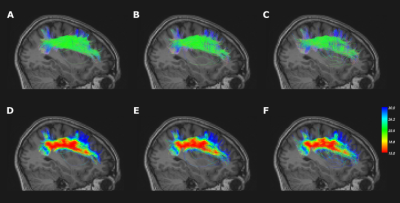
In the main white matter tracts, such as the frontoparietal part of the AF (Fig.4), an increase in maximum angle produces more stray and false positives treamlines. As shown in the bottom row of Fig.4, the angular map allowed for a greater angle near the cortex.
DiSCo phantom
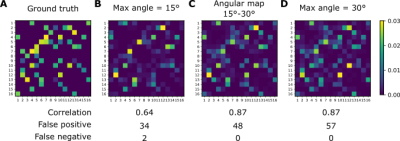
The connectivity matrices obtained in the DiSCo1 dataset in Fig.5 show the lowest correlation to the ground truth with a maximum angle of 15°. This angle also produced two false negatives between adjacent ROIs, requiring a high angle to connect. This configuration is similar to the geometry presented by U-fibers. Using the angular map or the 30° angle produced similar scores, except for a higher number of false positive streamlines in the 30° angle.
Conclusion
The results can be improved by refining the angular map created, such as using anatomical T1 information to better delimitate the subcortical white matter. Nonetheless, the inclusion of an adaptive maximum angle allows for a more accurate tracking of subcortical U-fibers along the cortical folds, without generating as many false positive streamlines as a global increase of the maximum angle. Incorporating this change into tractography algorithms might improve the accuracy of the tractograms produced, especially for subcortical fibers.Acknowledgements
No acknowledgement found.References
1. K.J. Riley, D.P. O’Neill, and S.F. Kralik. Subcortical U-Fibers: Signposts to the Diagnosis of White Matter Disease. Neurographics, 8(4):234–243, August 2018.
2. Owen R Phillips, Shantanu H. Joshi, Fabrizio Piras, Maria Donata Orfei, Mariangela Iorio, Katherine L. Narr, David W. Shattuck, Carlo Caltagirone, Gianfranco Spalletta, and Margherita Di Paola. The superficial white matter in Alzheimer’s disease: Superficial White Matter in Alzheimer’s Disease. Human Brain Mapping, 37(4):1321–1334, April 2016.
3. Ben Jeurissen, Maxime Descoteaux, Susumu Mori, and Alexander Leemans. Diffusion MRI fiber tractography of the brain. NMR in Biomedicine,32(4), April 2019.
4. Eleftherios Garyfallidis, Matthew Brett, Bagrat Amirbekian, Ariel Rokem, Stefan van der Walt, Maxime Descoteaux, Ian Nimmo-Smith, and Dipy Contributors. Dipy, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics, 8, February 2014.
5. Jelle Veraart, Dmitry S. Novikov, Daan Christiaens, Benjamin Adesaron, Jan Sijbers, and Els Fieremans. Denoising of diffusion MRI using random matrix theory. NeuroImage, 142:394–406, November 2016.
6. Elias Kellner, Bibek Dhital, Valerij G. Kiselev, and Marco Reisert. Gibbs-ringing artifact removal based on local subvoxel-shifts: Gibbs-Ringing Artifact Removal. Magnetic Resonance in Medicine, 76(5):1574–1581, November 2016.
7. Jesper L.R. Andersson and Stamatios N. Sotiropoulos. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage, 125:1063–1078, January 2016.
8. Maki S. Koyama, David O’Connor, Zarrar Shehzad, and Michael P. Milham. Differential contributions of the middle frontal gyrus functional connectivity to literacy and numeracy. Scientific Reports, 7(1):17548, December 2017.
9. Michael Andres, Xavier Seron, and Etienne Olivier. Contribution of Hand Motor Circuits to Counting. Journal of Cognitive Neuroscience, 19(4):563–576, April 2007.
10. Rahul S. Desikan, Florent Segonne, Bruce Fischl, Brian T. Quinn, Brad-ford C. Dickerson, Deborah Blacker, Randy L. Buckner, Anders M. Dale,R. Paul Maguire, Bradley T. Hyman, Marilyn S. Albert, and Ronald J.Killiany. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage,31(3):968–980, July 2006.
11. Demian Wassermann, Nikos Makris, Yogesh Rathi, Martha Shenton, RonKikinis, Marek Kubicki, and Carl-Fredrik Westin. The white matter query language: a novel approach for describing human white matter anatomy. Brain Structure and Function, 221(9):4705–4721, December 2016.
12. Gabriel Girard. The Diffusion-Simulated Connectivity Dataset, January 2022. Type: dataset.
13. Ben Jeurissen, Jacques-Donald Tournier, Thijs Dhollander, Alan Connelly,and Jan Sijbers. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage, 103:411–426, December 2014.
14. Robert E. Smith, Jacques-Donald Tournier, Fernando Calamante, and Alan Connelly. SIFT: Spherical-deconvolution informed filtering of tractograms.NeuroImage, 67:298–312, February 2013.
Figures