4160
White matter microstructure mapping using diffusion-only or diffusion-relaxation: protocol design and comparison of accuracy and precision1Radiology, NYU School of Medicine, NEW YORK, NY, United States, 2Diagnostic Radiology, Clinical Sciences, Lund University, Lund, Sweden
Synopsis
Keywords: Diffusion/other diffusion imaging techniques, Diffusion/other diffusion imaging techniques
Combining diffusion and relaxation is promising in probing the tissue microstructure in brain white matter. We designed an optimal diffusion-relaxation protocol with varying b-values, b-tensor shapes and echo times by minimizing the error of parameter estimation. We compared the Standard Model parameters estimated by diffusion-relaxation and diffusion-only data using sensitivity-specificity matrices and test-retest data on volunteers and found excellent agreement. With a comprehensive acquisition protocol, the Standard Model can accurately capture the signal content in white matter with diffusion MRI.Introduction
The Standard Model (SM) of diffusion is an overarching framework unifying many previously proposed models in white matter (WM) [1]. Yet, the estimation of Standard Model parameters remains a challenge due to the degeneracy in parameter estimation landscape [2]. Multidimensional diffusion MRI (dMRI) has been shown to alleviate the degeneracy in estimating SM parameters [3-4]. Recently, the SM framework has been extended to joint diffusion-relaxation modeling [5-8], which provides complementary information on compartmental relaxation. We designed an optimal acquisition protocol with multiple diffusion weightings ($$$b$$$), b-tensor shape ($$$b_{\Delta}$$$), and echo times (TE) by minimizing the mean-squared-error (MSE) of the estimation [9]. The sensitivity-specificity matrix (SSM) [10] along with test-retest human data is used to assess accuracy and precision of both the variable-TE protocol and its subset, a fixed-TE protocol.Theory
The SM assumes three axially symmetric Gaussian compartments with no exchange. The stick compartment, with signal fraction $$$f$$$, represents axons with parallel diffusivity $$$D_a$$$. The extra-axonal compartment reflects hindered diffusion with parallel and perpendicular diffusivities $$$D_e^{\parallel}$$$ and $$$D_e^{\bot}$$$. The free water compartment is characterized by signal fraction $$$f_{FW}$$$ and fixed diffusivity 3 μm2/ms. These compartments define a response function for a fiber fascicle:$$\mathcal{K}(b,b_{\Delta},\hat{u}) = fexp[ -D_{a}\sum_{ij}B_{ij}u_{i}u_{j}-TE/T_{2,a} ] + (1-f-f_{FW})exp[ -bD_{e}^{\bot}-(D_{e}^{\parallel}-D_{e}^{\bot} \sum_{ij}B_{ij}u_{i}u_{j}-TE/T_{2,e}) ] + f_{FW}exp [ -bD_{FW}-TE/T_{2,FW} ]$$
where $$$\hat{u}$$$ is the fiber segment orientation. $$$T_{2,a},\,T_{2,e},\,T_{2,FW}$$$ are the T2 values of the intra-axonal, extra-axonal and free water compartments, respectively. The SM signal is a convolution of the kernel and the fiber orientation distribution function (ODF): $$$S(B,TE)=s_{0}\int_{S^{2}}\mathcal{P}(\hat{u})\mathcal{K}(b,\,b_{\Delta},\hat{u})d\hat{u}$$$, where $$$s_0$$$ is the non-diffusion weighted signal. The ODF can factor in the basis of spherical harmonics: $$$\mathcal{P}(\hat{u})\approx1+\sum_{l=2,4,...}^{l_{max}}\sum_{m=-l}^{l}p_{lm}Y_{lm}(\hat{u})$$$. $$$p_2$$$, the norm of $$$p_{lm}$$$ for $$$l=2$$$, can be used to quantify ODF anisotropy.
Methods
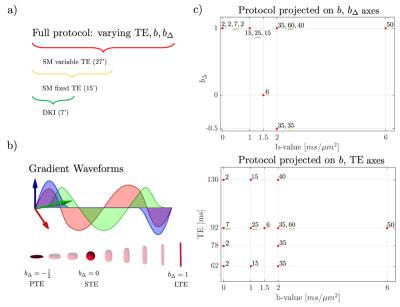
Protocol Design. Acquisition protocols were optimized by minimizing MSE of the estimation. Individual MSE expressions were analytically computed in [11]. For each shell, the optimization framework selected: diffusion weighting $$$b$$$, b-tensor shape $$$b_{\Delta}$$$ and TE. The 27-min full multi-$$$(b,\,b_{\Delta},\,TE)$$$ protocol was used to jointly estimate the diffusion-relaxation SM parameters, c.f. Fig. 1. A 15-min subset of this protocol acquired at TE=92ms was used for estimating fixed-TE SM parameters, of which a 7-min subset was a 2-shell DKI protocol.MRI and preprocessing. Six healthy volunteers (24-52yo, 3 female) underwent two repeated scan of brain diffusion MRI on Siemens Magnetom Prisma 3T systems, using a 64-channel head coil. The dMRI protocol (Fig. 1) consisted of Maxwell-compensated asymmetric waveforms [12] with isotropically distributed orientations. A non-diffusion-weighted image with reverse phase-encoding was acquired to correct for EPI-induced distortions [13]. Imaging parameters: TR>4s, bandwidth=1818Hz/Pixel, resolution 2.0mm isotropic, in-plane FOV = 220mm, GRAPPA and SMS acceleration factor = 2, partial fourier factor = 6/8. Data was then processed with the DESIGNER pipeline [14] for denoising [15], degibbsing [16-17], eddy current correction [18] to extract rotational invariants.
Parameter Estimation. We used a machine-learning based estimator to interpolate the mapping from rotational invariants to SM parameters [5]. To compare fractions between variable-TE and fixed-TE protocols, we weighed the variable-TE fractions with corresponding $$$e^{-TE/T_{2}}$$$ factors, and rescaled them to sum to 1. The sensitivity-specificity matrix (SSM) [10] was used to quantify the accuracy of parameter estimation: $$$\mathrm{SSM}_{ij}=\frac{\mu_{\theta_{i}}}{\mu_{\hat{\theta_{j}}}}\frac{\partial\hat{\theta}_{j}}{\partial\theta_{i}}$$$, where $$$\hat{\theta_{j}}$$$ is the estimated jth parameter, $$$\theta_{i}$$$ is the ground truth of the ith parameter. $$$\mu_{\theta}$$$ is the mean of a given SM parameter to make the SSM unit-less.
Coefficient of Variation. In addition, to evaluate precision of the human measurements, coefficients of variation (COV) were defined as $$$\mathrm{COV}=\frac{|x_{1}-x_{2}|}{x_{max}}$$$, where $$$x_{1}$$$ and $$$x_{2}$$$ are the voxelwise value of the scan and rescan, $$$x_{max}$$$ is the maximum physical value of a given SM parameter (1.0 for fractions, 3.0 μm2/ms for diffusivities, 150 ms for T2). COV was first calculated voxelwise and then averaged over WM for each subject.
Results
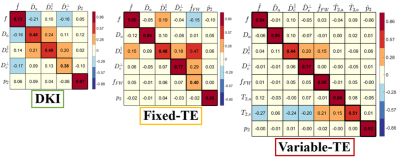
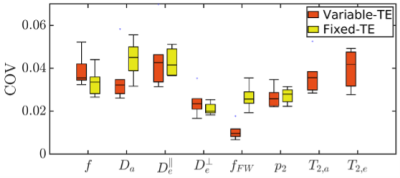
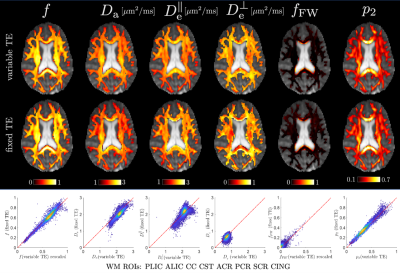
Fig. 2 shows the SSM of the 7-minute two-shell DKI protocol, 15-minute fixed-TE protocol and 27-minute variable-TE protocol. According to the SSM, multidimensional dMRI and high-b shells significantly improve the accuracy of estimating SM parameters for $$$f$$$, $$$D_{a}$$$ and $$$D_{e}^{\bot}$$$, as compared to conventional two-shell protocols. In addition, varying TE dramatically improves the accuracy of estimating $$$f_{FW}$$$. Fig. 3 shows the COV of the fixed-TE and variable-TE protocol for the six volunteers. The largest difference is in estimating $$$f_{FW}$$$, where the variable-TE protocol has only one third of the COV of the fixed-TE protocol. Fig. 4 shows the parametric maps and scatter plots of the fixed-TE and variable-TE protocol, which indicate SM parameters derived from these two protocols are in excellent agreement.Discussions and conclusions
We propose a multidimensional $$$(b,\,b_{\Delta},\,TE)$$$ protocol to estimate SM parameters as well as compartment relaxation parameters. Both the 15-min subset with fixed TE and the 27-min full protocol outperform for estimating SM parameters as compared to conventional two-shell protocols (Fig. 2). These two protocols have similar precision (Fig. 3) for all SM parameters, except that the variable-TE protocol dramatically improves the precision of $$$f_{FW}$$$, which suggests the difference in T2 helps separate the free water compartment from dMRI signal. Remarkably, SM parameters estimated by the fixed-TE protocol were in excellent agreement with that by variable-TE protocols. In summary, given a comprehensive acquisition protocol, the SM can accurately capture the dMRI signal content.Acknowledgements
This work was performed under the rubric of the Center for Advanced Imaging Renovation and Research (CAI24, https://www.cai2r.net), a NIBIB Biomedical Technology Research Center (NIH P41EB017183). This work has been supported by NIH under NINDS award R01NS088040 and NIBIB award R01EB027075.References
[1] Novikov, Dmitry S., et al. "Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI." NeuroImage 174 (2018): 518-538.
[2] Jelescu, Ileana O., et al. "Degeneracy in model parameter estimation for multi‐compartmental diffusion in neuronal tissue." NMR in Biomedicine 29.1 (2016): 33-47.
[3] Westin, Carl-Fredrik, et al. "Q-space trajectory imaging for multidimensional diffusion MRI of the human brain." Neuroimage 135 (2016): 345-362.
[4] Topgaard, Daniel. "Multidimensional diffusion MRI." Journal of Magnetic Resonance 275 (2017): 98-113.
[5] Veraart, Jelle, Dmitry S. Novikov, and Els Fieremans. "TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times." NeuroImage 182 (2018): 360-369.
[6] McKinnon, Emilie T., and Jens H. Jensen. "Measuring intra‐axonal T2 in white matter with direction‐averaged diffusion MRI." Magnetic resonance in medicine 81.5 (2019): 2985-2994.
[7] Lampinen, Björn, et al. "Towards unconstrained compartment modeling in white matter using diffusion‐relaxation MRI with tensor‐valued diffusion encoding." Magnetic resonance in medicine 84.3 (2020): 1605-1623.
[8] Gong, Ting, et al. "MTE-NODDI: Multi-TE NODDI for disentangling non-T2-weighted signal fractions from compartment-specific T2 relaxation times." Neuroimage 217 (2020): 116906.
[9] Reisert, Marco, et al. "Disentangling micro from mesostructure by diffusion MRI: a Bayesian approach." Neuroimage 147 (2017): 964-975.
[10] Liao, Ying, et al. "Liao, Ying, et al. "How to understand diffusion MRI changes in the white matter of Multiple Sclerosis patients?."." Proceedings of the 31st Annual Meeting of ISMRM. Vol. 981. 2022.
[11] Coelho Santiago, et al. "How do we know we measure tissue parameters, not the prior." Proceedings of the 30th Annual Meeting of ISMRM. Vol. 397. 2021.
[12] Szczepankiewicz, Filip, Carl‐Fredrik Westin, and Markus Nilsson. "Maxwell‐compensated design of asymmetric gradient waveforms for tensor‐valued diffusion encoding." Magnetic resonance in medicine 82.4 (2019): 1424-1437.
[13] Andersson, Jesper LR, Stefan Skare, and John Ashburner. "How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging." Neuroimage 20.2 (2003): 870-888.
[14] Ades-Aron, Benjamin, et al. "Evaluation of the accuracy and precision of the diffusion parameter EStImation with Gibbs and NoisE removal pipeline." Neuroimage 183 (2018): 532-543.
[15] Veraart, Jelle, et al. "Denoising of diffusion MRI using random matrix theory." Neuroimage 142 (2016): 394-406.
[16] Kellner, Elias, et al. "Gibbs‐ringing artifact removal based on local subvoxel‐shifts." Magnetic resonance in medicine 76.5 (2016): 1574-1581.
[17] Tournier, J-Donald, et al. "MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation." Neuroimage 202 (2019): 116137.
[18] Smith, Stephen M., et al. "Advances in functional and structural MR image analysis and implementation as FSL." Neuroimage 23 (2004): S208-S219.
Figures