4109
Signal-to-noise Ratio Enhancement of 31P Magnetic Resonance Spectroscopy using a Pre-trained Deep Learning Model1Department of Health Sciences and Technology, GAIHST, Gachon University, Incheon, Korea, Republic of, 2Lee Gil Ya Cancer & Diabetes Institute, Gachon University, Incheon, Korea, Republic of, 3Department of Radiology, University Medical Centre Utrecht, Utrecht, Netherlands, 4Institute for Diagnostic and Interventional Neuroradiology, Support Center for Advanced Neuroimaging (SCAN), University of Bern, Bern, Swaziland, 5Translational Imaging Ceter, sitem-insel AG, Bern, Switzerland
Synopsis
Keywords: Data Processing, Spectroscopy, Non-Proton, Animals, Brain, Precision & Accuracy
We demonstrate the feasibility of a novel denoising approach utilizing a pretrained deep learning model with multiscale local polynomial smoothing for single voxel 31P MRS data in the mice brain at 9.4T. We evaluated the low-rank denoising, one of the popular methods and the proposed method using LCModel to compare their performance. Both methods resulted in improved signal-to-noise ratio and decreased uncertainty (Cramer-Rao Lower Bounds). In this work, the suggested method outperformed in signal-to-noise ratio enhancement.Introduction
Single voxel 31P MRS is a non-invasive technique that has been used to study metabolic changes in the brains of small animals1,2. However, data acquisition of low-concentration 31P metabolites from small brain volumes are technically challenging because of insufficient SNR in limited scan time, making quantitative analysis more difficult. While many methods have been proposed to improve SNR for MRS(I)3-6, limited efforts have been spent on single voxel 31P MRS denoising and previously introduced methods were difficult to implement due to lack of easy to access publicly available resources. Therefore, we suggest a preliminary novel approach to improve the SNR of single voxel 31P MRS using a combination of a pretrained image denoising convolutional neural network, ‘dnCNN’7 and multiscale local 1D polynomial transform, ‘mlptdenoise’8 MATLAB built-in functions. We found that this method could enhance 157.82% SNR increase on average compared to unsmoothed noisy data.Methods
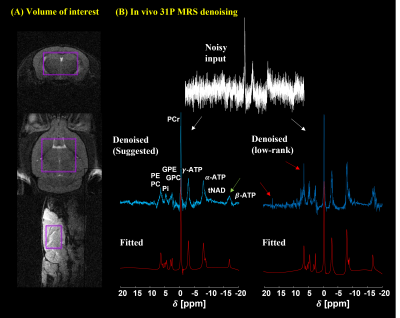
All MR measurements were acquired on a 9.4 T MRI system with ParaVision 6.0 software (Bruker BioSpin Corporation, Billerica, MA, USA) at Core-facility for Cell to In-vivo imaging. To test our method, we first generated a simulation 31P spectrum and a basis set based on previously reported information9 using Spinach toolbox10. The basis set consisted of 13 basis spectra (PCr, α-ATP, β-ATP, ɣ-ATP, Pi, NADH, NAD+, PE, PC, GPE, GPC, MP, and DPG). The in vivo 31P MRS data (N=13) were acquired using a dual-tuned 1H/31P surface coil of 20 mm with an Image Selected In Vivo Spectroscopy11 pulse sequence. The low-rank denoising was performed using ‘mrs-denoising-tools’ Python package4 and the suggested method using MATLAB built-in functions as shown in Figure 1. The Hankel matrix was constructed using single-voxel time-domain free induction decay (FID) data to generate ‘image’. The matrix size (W x W+1) of the Hankel matrix was determined as the half-length of the FID signal and dimension reduction parameter (r) as the number of metabolites (e.g., r=13 for 31P MRS). The SNR is defined here as the ratio between the maximum in the spectrum (e.g., PCr) and twice the rms residuals from LCModel output.Results
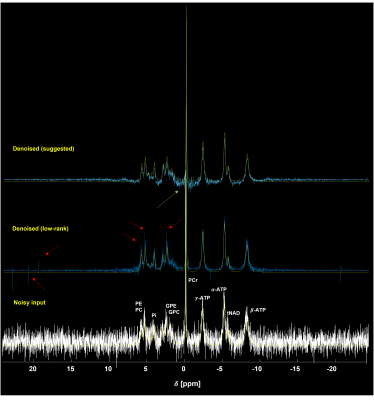
Figure 2 shows the 31P simulation spectrum at 9.4 T stacked with denoised data using the low-rank and the suggested methods. As can be seen, the low-rank yielded slightly more noisy output with some spurious peaks (red arrows) than the suggested method that yielded less noisy output but seemed to have some loss of information. Figure 3 shows single voxel in vivo 31P MRS mouse brain data. The low-rank method and the suggested method effectively reduced noise from noisy input data. Similar to the simulation data, the low-rank method produced some spurious peaks (red arrows) and performed less noise removal. On the other hand, the suggested method further removed noise although it was observed that metabolite information loss appeared as the peak intensity decreased (green arrow). Figure 4 shows average SNR values of in vivo 31P MRS data (N=13). Compared with noisy input data, both methods greatly enhanced the SNR. The low-rank increased by 115.38% on average compared to noisy data (p<0.01), and the suggested method increased SNR by 157.82% (p<0.01). The suggested method increased SNR by 19.7% more compared to low-rank (p<0.01). Figure 5 shows average CRLB values of in vivo 31P MRS data. Both methods greatly reduced the CRLBs from noisy input data, there were no statistically significant differences between the suggested and low-rank methods except for α-ATP, β-ATP, NAD+, and NADH (p<0.05).Discussion
The suggested method shows encouraging preliminary results for single voxel 31P MRS denoising at 9.4 T. Although the ‘DnCNN’ was developed for image denoising7, it could be applied for 1D spectrum by changing data representation (e.g., Hankel matrix form), we further reduced noise using ‘mlptdenoise’. The suggested method is easy to implement by utilizing MATLAB built-in functions and this method outperformed in SNR enhancement than low-rank method that resulted in artifacts and weak denoising performance. However, we also observed several limitations of this method such as remaining noise near PCr, loss of metabolite peak heights (Figure 2 and Figure 3, green arrows) that might be due to current limitations of the pre-trained ‘DnCNN’ model for 31P MRS data.Conclusion
The preliminary results in this study revealed encouraging denoising performance comparable to low-rank noise reduction and it might be further improved using transfer learning strategies such as re-training, half-freezing, and fine-tuning with 31P MRS data.Acknowledgements
This project has received funding from [Bio & Medical Technology Development Program of the National Research Foundation funded by the Korea government (MSIT) (grant No. 2020M3A9E4104384), and the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement (No. 813120).References
[1] V. Rackayova, O. Braissant, V.A. McLin, C. Berset, B. Lanz, C. Cudalbu, “1H and 31P magnetic resonance spectroscopy in a rat model of chronic hepatic encephalopathy: in vivo longitudinal measurements of brain energy metabolism,” Metab Brain Dis 31, 1303-1314, (2016).
[2] D.M. Lindquist, R.H. Asch, J.D. Schurdak, R.K. McNamara, “Effects of dietary-induced alterations in rat brain docosahexaenoic acid accrual on phospholipid metabolism and mitochondrial bioenergetics: An in vivo 31P MRS study,” J Psychiatr Res. 95, 143-146, (2017).
[3] J.A. Cadzow, “A Composite Property Mapping Algorithm,” IEEE Trans Acoust, 36, 49-62, (1988).
[4] W.T. Clarke, M. Chiew, “Uncertainty in denoising of MRSI using low-rank methods,” Magn Reson Med, 87, 574-588, (2022).
[5] O.A. Ahmed, “New denoising scheme for magnetic resonance spectroscopy signals,” IEEE Trans Med Imaging,” 24, 809-816, (2005).
[6] F. Lam, Y. Li, X. Peng, “Constrained Magnetic Resonance Spectroscopic Imaging by Learning Nonlinear Low-Dimensional Models,” IEEE Transactions on Medical Imaging 39, 3, (2020).
[7] K. Zhang, W. Zuo, “Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising,” IEEE Transaction on Image Processing 26 no. 7, (2017) 1057-7149
[8] M. Jansen, “Multiscale Local Polynomial Smoothing in a Lifted Pyramid for Non-Equispaced Data,” IEEE Transaction on Signal Processing 61, no. 3, (2013).
[9] D. K. Deelchand, T.-M. Nguyen, X.-H, F. Mochel, and P.-G. Henry, “Quantification of in vivo 31P nmr brain spectra using lcmodel,” NMR in Biomedicine 28 no. 6, 633-641, (2015).
[10] H.J. Hogben, M. Krzystyniak, G.T.P. Charnock, P.J. Hore, I. Kuprov, “Spinach – A software library for simulation of spin dynamics in large spin systems,” Journal of Magnetic Resonance 208, 179-194, (2011).
[11] R.J. Ordidge, A. Connelly, J.A.B. Lohman, “Image-selected In Vivo spectroscopy (ISIS). A new technique for spatially selective nmr spectroscopy,” Journal of Magnetic Resonance, 66, 283-294, (1986).
Figures