Synopsis

Keywords: High-Field MRI, RF Pulse Design & Fields

The T₂*contrast specifically benefits from 7T human MRI systems and is frequently used in Neuroimaging. However, B₁⁺ and B₀ inhomogeneity at 7T limits the effectiveness of the T₂*. A method originally proposed to minimize channel effects in the field of telecommunications, was adopted to a dual channel parallel transmission (pTx) human 7T MRI system. Final images are obtained by the unique combination of four small angle GRE acquisitons with adjusted flip angles for each channel. The proposed method is easy to implement, robust and provides homogeneous T₂* images of the whole brain.

Introduction

The contrast specifically benefits from 7T human MRI systems and has been used as diagnostic/prognostic marker for Alzheimers Disease¹, Multiple Sclerosis^2,3 and Parkinsons Disease⁴. However, transmit field ($$$B_1^+$$$) and main static magnetic field ($$$B_0$$$) inhomogeneity ($$$Δ$$$) at 7T^5,6 can severely degrade the image quality.
In this work, the Bilateral Orthogonality Generating Acquisitions method originally proposed to eliminate channel effects in the field of telecommunication^7,8 was adopted to a dual channel parallel transmission (pTx) human 7T MRI system. It is demonstrated that homogeneous contrast images can be obtained without the requirement for prior mapping of and . In the first step, two spoiled gradient recalled echo (GRE) images with adjusted flip angles combined in order to generate an orthogonality between acquisitions have to be obtained, similar to the space time diversity method in wireless communications^7,8. In addition, two single channel GRE acquisitions are utilized to calculate images without $$$B_1^+$$$ and $$$B_0$$$ inhomogeneity effects.

Methods

For a dual channel pTX system using the same block pulse with amplitude $$$\beta$$$ for both channels without any gradient trajectory the flip angle in a single pixel $$$i$$$ can be written as $$$ \alpha ^i = (s_1^i e^{j \theta_1} +s_2^i e^{j \theta_2} )c_{\Delta B_0}^i e^{-j\phi_{\Delta B_0}^i} \beta$$$⁶. $$$s_1$$$ and $$$s_2$$$ are the channel specific transmit sensitivities and $$$\theta_1$$$ and $$$\theta_2$$$ are the transmission phases of each channel. Amplitude and phase effects of $$$\Delta B_0$$$ are $$$c_{\Delta B_0}^i = \gamma m_0 \Delta t {sin(0.5 N_t \gamma \Delta B_0^i \Delta t )}/{sin(0.5 \gamma \Delta B_0^i \Delta t )}$$$ and $$$\phi_{\Delta B_0}^i = 0.5(N_t +1)\gamma\Delta B_0^i\Delta t$$$. Defining $$$q_{1,2}^i=s_{1,2}^ic_{\Delta B_0}^ie^{-j\phi_{\Delta B_0}^i}e^{\theta_{1,2}} $$$ the flip angle expression including both and inhomogeneity effects simplifies to $$$\alpha^i_{1,2}=q_{1,2}^i\beta$$$.
Using the small tip angle approximation⁶, spoiled GRE signal equation⁹ can be simplified to $$$S = \rho E_2^* \alpha $$$ , where$$$\rho$$$ is the proton density and $$$E_2^* = e^{-TE/T_2^*}$$$ . For a dual channel pTx system, spoiled GRE signal can be further written as $$$S = \rho E_2^* (q_1+q_2)\beta$$$.
For the suggested method the first two input images are defined as $$$S_1 = \rho E_{2,1}^* (q_1+q_2)\beta$$$ and $$$S_2 = \rho E_{2,1}^* (- q_1+q_2)\beta^*$$$. Since the transmit phase of the pulses is included in $$$\theta_{1,2}$$$, $$$\beta$$$ defines only the real valued amplitude of the block pulse resulting in $$$\beta = \beta^*$$$ , which then leads to $$$S_2 = \rho E_{2,1}^* (- q_1+q_2)\beta$$$ . The negative flip angle is implemented via the additional transmit phase of $$$\pi$$$ for the first channel.
The second two acquisitions utilize the same block pulses, but channels are used individually, resulting in $$$S_{1,2} = \rho E_{2,2}^*q_{1,2}\beta$$$ . By combining the four signals as in⁷, $$$C_1$$$ and $$$C_2$$$ can be defined as $$$C_1 = S_3^*S_1+S_4S_2^*$$$ and $$$C_2 = S_4^*S_1-S_3S_2^*$$$. In matrix format, combined signals can be written as follows.
$$ \left[ \begin{matrix}C_1\\C_2\end{matrix}\right] =\rho^2E_{2,1}^*E_{2,2}^*\left[\begin{matrix} q_1^*\beta&q_2\beta\\q_2^*\beta&-q_1\beta\end{matrix}\right]\left[ \begin{matrix}q_1& q_2\\q_2^*& - q_1^*\end{matrix}\right]\left[ \begin{matrix}\beta\\\beta\end{matrix}\right] = \rho^2E_{2,1}^*E_{2,2}^* \beta^2\left[\begin{matrix}|q_1|^2+|q_2|^2\\|q_1|^2+|q_2|^2\end{matrix}\right]$$ Orthogonality of $$$C_1$$$ and $$$C_2$$$ is only valid if there is no phase mismatch between transmit and receive channels. Since in MRI often different transmit and receive coils are used and complex transmit and receive sensitivities do generally not match. This assumption does not hold and results in phase errors. Due to a lack of orthogonality the obtained $$$T_2^*$$$ images from $$$C_1$$$ and $$$C_2$$$ show distortions. In order to eliminate effects of the phase errors, magnitudes of $$$C_1$$$ and $$$C_2$$$ have to be averaged before obtaining the final $$$T_2^*$$$ image which is then calculated as $$$I = \frac{0.5\sqrt{C_1^*C_1+C_2^*C_2}}{S_3^*S_3+S_4^*S_4}$$$ . This, also enables the use of a separate receive coil.
For the acquisition of the data, a 7T Philips Healthcare whole body human MRI system with two transmit channels is used along with the 32 channel receive Nova Medical head coil as receive coil. For two healthy volunteers, the four above described 3D spoiled GRE acquisitions were acquired each with voxel size of $$$1.5x1.5x1.5 mm$$$, $$$144x144x100$$$ acquisition matrix and $$$5^o$$$ flip angle. $$$TE_1/TR = 20/22 ms $$$ with 2 averages and $$$TE_2/TR = 1.28/4.2 ms$$$ with 5 averages are used for first two and last two acquisitions. The final $$$T_2^*$$$image has the effective echo time of $$$TE_{eff} = TE_1-TE_2$$$ and is free of effects of $$$B_1^+$$$ and $$$\Delta B_0$$$.

Results

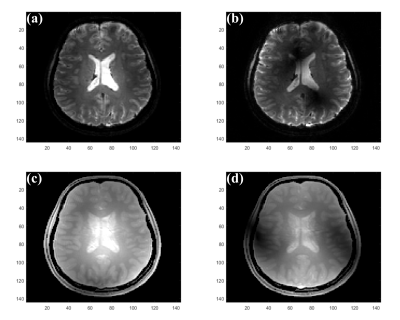
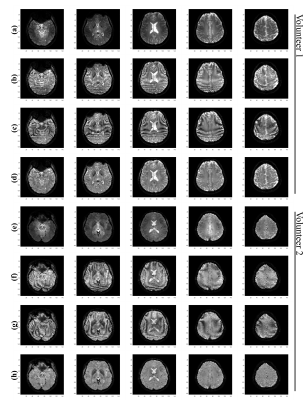
Figure 1 illustrates the images that have to be acquired as input for the proposed method. Rows (d,h) of Figures 2-4 demonstrate that the proposed method provides whole brain $$$T_2^*$$$ images without the inhomogeneity effects of $$$B_1^+$$$ and $$$B_0$$$ and in contrast to the CP mode image in rows (a,e). Rows (b,f) and (c,g) in Figures 2-4, shows that $$$T_2^*$$$ images obtained solely from $$$C_1$$$ and $$$C_2$$$ are severely affected from the phase errors in all orientations but rows d and h in these figures shows that the final images obtained via amplitude combination of $$$C_1$$$ and $$$C_2$$$ is not affected. Figure 5 shows representative zoomed versions of the final $$$T_2^*$$$ images.

Discussion and Conclusion

This newly introduced method is easy to implement, robust and provides homogeneous $$$T_2^*$$$ images of the whole brain. Herein it is implemented for dual-channel pTx systems but an extension to 8 channel pTx systems is underway.

Acknowledgements

This work was funded by Cancer Prevention and Research Institute of Texas (CPRIT) RR180056 and was performed under the rubric of the Advanced Imaging Research Center, UT Southwestern Medical Center.