4049
Self-Supervised Denoising for Longitudinal MRI1Medical Biophysics, University of Toronto, Toronto, ON, Canada, 2Physical Sciences Platform, Sunnybrook Research Institute, Toronto, ON, Canada
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Cancer, Denoising, Self-Supervised
In MR guided radiation therapy, images of patients are acquired daily. However, scan times are long to acquire images with an acceptable SNR for treatment planning and adaptation. In this study we test a self-supervised machine learning based approach for denoising data that can utilize previous scans of the same patient to improve quality of the denoised image. Results on a numerical phantom and clinical images are presented and compared to a popular non-machine learning denoising algorithm.Introduction
MRI-linear accelerators (MR-Linac) allow for daily imaging during sequential radiation treatment (RT) sessions 1,2. Current treatment approaches use a single structural image for daily target adaptation3. Quantitative MRI techniques show promise for adding to personalized treatments, but long scan times to achieve acceptable SNR remain a challenge4,5. Image denoising can improve low SNR of data acquired with high acceleration factors or varied contrast encodings (e.g diffusion). A unique aspect of MR-Linac imaging is the availability of longitudinal images which could aid in image denoising.Convolutional neural network-based image denoising methods demonstrate improved performance compared to conventional denoising methods. However, supervised methods require many clean/noisy image pairs for training, which are difficult to acquire. Self-supervised methods 6–9 do not require labeled data and can be trained on noisy examples alone. Self2Self9 is a unique self-supervised method that can be trained with as little as a single noisy image.
In this study, the Self2Self model was used to denoise a numerical phantom and MR-Linac T1w and FLAIR images of brain tumour patients, and quantitatively evaluate whether denoising performance improves when including previous scans with changing anatomy and additional imaging contrasts.
Methods
Data:Phantom: A changing tumour was simulated by modifying a Shepp-Logan phantom10 (matrix size 256x256) with a disk of varying size and shape (Fig.2). The intensity, height, and width of the simulated tumour was randomly chosen to either increase or decrease (to simulate a progressive or regressive tumour) randomly by 0-10% five time to represent one weeks worth of treatment fractions, 20 simulated phantoms were analyzed with different initial tumour placements.
MR-Linac: Glioblastoma patients (N=20) undergoing RT on a 1.5T Elekta Unity MR-Linac (Elekta AB, Stockholm) were imaged with T1w and FLAIR sequences. For each patient five sequential daily scans were used. T1w images had resolution 0.7x0.7x1.1 mm3 reconstruction matrix size 384x384 and acquisition matrix size 247x247. FLAIR images had resolution 0.6x0.6x2.6 mm3 with reconstruction matrix size 480x480 and acquisition matrix size 217x217.
Image Processing:
For each patient, image volumes were rigidly registered to the first treatment session T1w scan using FSL FLIRT 11,12. Each slice was resampled to the acquisition matrix size and intensities scaled to [0-1] before being split into 2D slices for input to the network. Phantom data was generated with intensities between 0-1. For both datasets, zero mean additive gaussian white noise was added at levels $$$\sigma = 15%$$$ and $$$\sigma =40%$$$.
Model:
The Self2Self method is as follows. Let a single noisy image be $$$y=x+n$$$ where $$$x$$$ is the clean image, and $$$y$$$ is corrupting noise. Let $$$\hat{y_m}$$$ be a set of $$$y$$$ that have been Bernoulli sampled $$$M$$$ times with $$$p=0.3$$$, and $$$\bar{y_m}$$$ be the complementary set of filtered voxels. The model $$$F_\theta$$$ is trained to predict the masked voxels with the remaining voxels $$$Loss=|F_\theta (\hat{y_m})-\bar{y_m}|^2$$$. Then, during testing, $$$N$$$ new Bernoulli samples are made, and each is used to generate a prediction $$$\tilde{x_n}$$$. The average of all $$$\tilde{x_n}$$$ is the denoised result. The model architecture is shown in Fig.1. Each Partial Conv and Conv layer has kernel size 3x3, stride of 1, and zero padding of 1. The Adam optimizer13 is used for training with learning rate =1e-4 and 10,000 training steps. During testing 100 samples were averaged to generate the denoised result. Our implementation requires approximately 6 minutes to process a 2D slice with an Nvidia Titan XP GPU.
Experiments:
The model was evaluated by denoising zero-mean additive gaussian white noise on both datasets. Structural similarity (SSIM) was calculated over the signal region (no background), and for the MR-Linac dataset also over the gross tumour (GTV) and clinical target volume (CTV) from the clinical treatment plan. Each slice was denoised individually (“Self2Self-Single”) or as part of an image stack with five time points as input channels (“Self2Self-Multi”). The popular BM3D 14 algorithm was included as a baseline comparison.
Results
On both simulated phantom data Fig 2, and MR-Linac data Fig 3, the self-supervised model was able to denoise data with simulated zero-mean gaussian noise. SSIM results are presented in Fig 5. When denoising the phantom data, the additional scans in the Self2Self-Multi model provided useful context to resolve the three small circles, which when $$$\sigma=40%$$$ noise was added were unable to be resolved by the Self2Self-Single model. In the MR-Linac data, denoised outputs showed a high SSIM compared to BM3D across the entire brain, as well as the GTV and CTV, which are dynamic from timepoint to timepoint due to the tumour progression.Discussion and Conclusion:
A self-supervised denoising model capable of training on a single image was applied to simulated data and data from glioblastoma patients undergoing MR-guided radiation therapy after images were corrupted by artificial additive gaussian white noise. Denoised data was accurate compared to the ground truth and improved when longitudinal data from the same subject was provided.Acknowledgements
No acknowledgement found.References
1. Lagendijk JJW, Raaymakers BW, Van Den Berg CAT, Moerland MA, Philippens ME, Van Vulpen M. MR guidance in radiotherapy. Phys Med Biol. 2014;59(21):R349-R369. doi:10.1088/0031-9155/59/21/R349
2. Raaymakers BW, Raaijmakers AJE, Kotte ANTJ, Jette D, Lagendijk JJW. Integrating a MRI scanner with a 6 MV radiotherapy accelerator: Dose deposition in a transverse magnetic field. Phys Med Biol. 2004;49(17):4109-4118. doi:10.1088/0031-9155/49/17/019
3. de Mol van Otterloo SR, Christodouleas JP, Blezer ELA, et al. The MOMENTUM Study: An International Registry for the Evidence-Based Introduction of MR-Guided Adaptive Therapy. Front Oncol. 2020;10:1328. doi:10.3389/FONC.2020.01328/BIBTEX
4. Winkel D, Bol GH, Kroon PS, et al. Adaptive radiotherapy: The Elekta Unity MR-linac concept. Clin Transl Radiat Oncol. 2019;18:54-59. doi:10.1016/J.CTRO.2019.04.001
5. Goodburn RJ, Philippens MEP, Lefebvre TL, et al. The future of MRI in radiation therapy: Challenges and opportunities for the MR community. Magn Reson Med. 2022;88(6):2592-2608. doi:10.1002/MRM.29450
6. Lehtinen J, Munkberg J, Hasselgren J, et al. Noise2Noise: Learning Image Restoration without Clean Data. Published online 2018. Accessed July 17, 2022. http://r0k.us/graphics/kodak/
7. Krull A, Buchholz T-O, Jug F. Noise2Void-Learning Denoising from Single Noisy Images. Accessed July 17, 2022. http://celltrackingchallenge.net/
8. Xu J, Adalsteinsson E. Deformed2Self: Self-Supervised Denoising for Dynamic Medical Imaging.
9. Quan Y, Chen M, Pang T, Ji H. Self2Self With Dropout: Learning Self-Supervised Denoising From Single Image.
10. Shepp LA, Logan B. The Fourier Reconstruction Of A Head Section. IEEE Trans Nucl Sci. 1974;NS-21.
11. Jenkinson M, Bannister P, Brady M, Smith S. Improved Optimization for the Robust and Accurate Linear Registration and Motion Correction of Brain Images. Neuroimage. 2002;17(2):825-841. doi:10.1006/NIMG.2002.1132
12. Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5(2):143-156. doi:10.1016/S1361-8415(01)00036-6
13. Kingma DP, Ba JL. Adam: A method for stochastic optimization. In: 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings. International Conference on Learning Representations, ICLR; 2015.
14. Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans Image Process. 2007;16(8):2080-2095. doi:10.1109/TIP.2007.901238
Figures
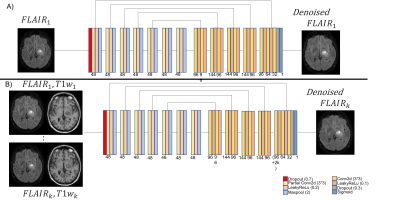

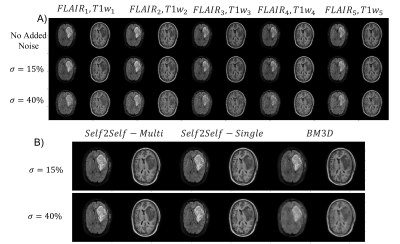
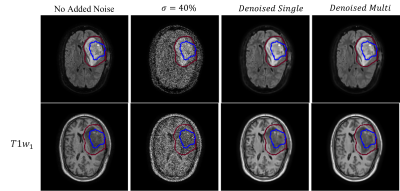
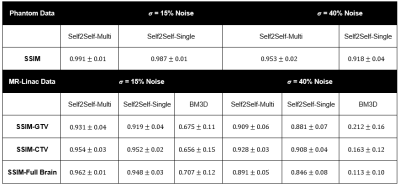
Fig.5 Results Table
Structural similarity is reported for denoised images (+/- is the standard deviation of all samples samples in the group).