4046
Quantitative evaluation of denoising algorithms without noise-free ground-truth data
Laura Pfaff1,2, Fabian Wagner1, Julian Hossbach1,2, Elisabeth Preuhs1, Dominik Nickel2, Tobias Wuerfl2, and Andreas Maier1
1Pattern Recognition Lab, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2Magnetic Resonance, Siemens Healthcare GmbH, Erlangen, Germany
1Pattern Recognition Lab, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2Magnetic Resonance, Siemens Healthcare GmbH, Erlangen, Germany
Synopsis
Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence
In MRI, the quantitative evaluation of denoising methods is often limited due to the lack of noise-free ground-truth data. We show how to still approximate the quality metrics mean squared error (MSE) and peak signal-to-noise-ratio (PSNR) without access to ground-truth data by using Stein’s unbiased risk estimator (SURE). The proposed method can be employed to evaluate learning- and non-learning-based denoising approaches, assuming an additive Gaussian noise model with known distribution. Our experiments further reveal that the accuracy of our evaluation method increases with the number of test samples available.Introduction
Image denoising steps are commonly employed to reduce the noise naturally present in MR images. In recent years, conventional denoising algorithms such as BM3D1 were outperformed by deep learning-based methods allowing data-driven optimization. These approaches are commonly trained in a supervised manner, requiring data pairs of noisy input and noise-free target images. Since the acquisition of noise-free images is usually infeasible in the context of medical imaging, multiple unsupervised methods were proposed that can be trained without clean targets. For instance, previous works incorporated Stein’s unbiased risk estimator (SURE)2 as a loss function to train a denoising network in an unsupervised manner by approximating the mean squared error (MSE) between the denoised and unknown noise-free images for additive Gaussian noise models with known distribution3,4.Despite their major advantage, it is often difficult to quantitatively evaluate unsupervised denoising approaches, as noise-free ground-truth data is required to calculate commonly used quality metrics. We show that SURE can not only be implemented as a loss function during training but also to replace the supervised evaluation metrics MSE and peak signal-to-noise ratio (PSNR). In this way, we can quantitatively evaluate the predictions of a neural network or a non-learning-based method without any noise-free data.
Methods
SURE is an estimate of the MSE between the unknown mean $$$\boldsymbol{x}$$$ of a Gaussian distributed signal $$$\boldsymbol{y}$$$ and its estimate $$$\hat{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{y})$$$. In previous works, SURE was employed for image denoising tasks by considering the unknown noise-free image $$$\boldsymbol{x}$$$ to be the mean of the noisy image $$$\boldsymbol{y}$$$ corrupted with additive, zero-mean Gaussian noise with known distribution3,4.The noise in complex-valued reconstructed MR images acquired using parallel imaging techniques can be modeled as a spatially variant Gaussian distribution5. Therefore, we use an adapted version of SURE that considers a noise map $$$\boldsymbol{\sigma}$$$ indicating the standard deviation of the noise for every pixel6.
Consequently, SURE can be used to estimate the expectation of the MSE between the predictions of a denoising algorithm $$$\boldsymbol{f}(\boldsymbol{y})$$$ and the noise-free ground truth $$$\boldsymbol{x}$$$ as follows:
$$\text{E}_{\boldsymbol{x}}\Big\{\,\frac{1}{D}\Vert\boldsymbol{f}(\boldsymbol{y})-\boldsymbol{x}\Vert^2 \Big\}\,=\text{E}_{\boldsymbol{x}}\Big\{\,\frac{1}{D}\Bigl(\Vert\boldsymbol{f}(\boldsymbol{y})-\boldsymbol{y}\Vert^2 -\sum\nolimits_{d=1}^D\sigma_d^2+2\text{div}_{\boldsymbol{y}} (\boldsymbol{\sigma^2}\odot\boldsymbol{f}(\boldsymbol{y}))\Bigr)\Big\}\,\,,$$
where $$$\odot$$$ denotes element-wise multiplication and $$$D$$$ is the number of pixels. In practice, we can approximate the expected value $$$\text{E}_{\boldsymbol{x}}$$$ by computing the average over a set of $$$N$$$ images:
$$\frac{1}{N}\sum\nolimits_{n=1}^N\frac{1}{D}\Vert\boldsymbol{f}(\boldsymbol{y}_n)-\boldsymbol{x}_n\Vert^2=\frac{1}{N}\sum\nolimits_{n=1}^N\Biggl(\frac{1}{D}\Bigl(\Vert\boldsymbol{f}(\boldsymbol{y}_n)-\boldsymbol{y}_n\Vert^2-\sum\nolimits_{d=1}^D\sigma_d^2+2\text{div}_{\boldsymbol{y}_n}(\boldsymbol{\sigma}_n^2\odot \boldsymbol{f}(\boldsymbol{y}_n))\Bigr)\Biggr)\,\,.$$
Since it is often inefficient to calculate the divergence term $$$\text{div}_{\boldsymbol{y}}$$$ analytically, especially in the case of neural networks, we approximate the divergence using a stochastic derivative7:
$$\text{div}_{\boldsymbol{y}}(\boldsymbol{\sigma}^2\odot \boldsymbol{f}(\boldsymbol{y}))\approx \boldsymbol{b}^T\bigg(\,\boldsymbol{\sigma^2}\odot\Big(\,\frac{\boldsymbol{f}(\boldsymbol{y}+\epsilon \boldsymbol{b})-\boldsymbol{f}(\boldsymbol{y})}{\epsilon}\Big)\,\bigg)\,\,,$$
where $$$\boldsymbol{b}$$$ is a zero-mean random vector with unit variance and $$$\epsilon$$$ is a fixed small value. The PSNR can then be calculated as follows:
$$\text{PSNR}=10\log_{10}{\frac{L^2}{\text{SURE}}}\,\,,$$
where $$$L$$$ denotes the intensity range of the data.
A side-by-side comparison between the actual MSE and PSNR and the SURE-based estimate requires pairs of clean and noisy images and the corresponding noise maps. We used the simulated BrainWeb20 MR data base8, consisting of 20 anatomical models of normal brains to create a set of 1,200 noise-free T2-weighted slice images as ground-truth data. We then added spatially variant Gaussian noise using 20 dedicated sets of noise maps to generate the noisy images.
We trained the standard deep neural network architectures U-Net9 and DnCNN10 in PyTorch using SURE as a loss function and the Adam optimizer with a learning rate of 3ˑ10-4. Then, we calculated MSE, PSNR, and SURE-based estimates of MSE and PSNR for both network architectures as well as the non-learning-based method BM3D1. We further analyzed the influence of the number of test images on the metric accuracy by computing the respective metrics considering $$$N$$$ slices with $$$N\in\left[1,235\right]$$$ for the U-Net only.
Results
The comparison between MSE and SURE-based evaluation metrics calculated over the entire test set is presented in Table 1. Table 2 shows the results computed for one randomly selected image slice. We found that the mean deviation between PSNR and SURE-based PSNR for images of the test data set was 0.26 dB. The influence of the number of test images is illustrated in Figure 1.Discussion
The results listed in Table 1 indicate that calculating the MSE and PSNR between network output and ground truth, or between noisy observation and ground truth can be replaced by computing SURE-based metrics without noise-free reference when averaged over a data set. In contrast, the results shown in Table 2 suggest that an accurate representation of MSE and PSNR using SURE cannot be guaranteed for individual slice images. Figure 1 further reveals that the accuracy of the predicted PSNR increases with the number of test images.Calculating the SURE-based metrics requires the availability of spatially resolved noise maps. For complex-valued MR images, an accurate Gaussian noise model can be determined by propagating the noise distribution in k-space measured with a noise adjustment scan through the entire image reconstruction pipeline6.
Conclusion
Our experiments revealed that SURE can be used to compute quantitative image quality metrics that are consistent with the supervised MSE and PSNR metrics on a test data set without noise-free ground-truth images. This makes the proposed method particularly interesting for unsupervised denoising tasks and can be used to quantitatively compare the performance of different network architectures or conventional, non-learning-based methods if accurate noise maps are available.Acknowledgements
No acknowledgement found.References
- Song B, Duan Z, Gao Y et al. Adaptive BM3D algorithm for image denoising using coefficient of variation. In 2019 22nd International Conference on Information Fusion (FUSION), pages 1–8, 2019.
- Stein C. Estimation of the mean of a multivariate normal distribution. The Annals of Statistics, 9(6):1135–1151, 1981.
- Metzler C, Mousavi A, Heckel R et al. Unsupervised learning with Stein’s unbiased risk estimator. arXiv preprint arXiv:1805.10531, 2018.
- Soltanayev S, Chun SY. Training and refining deep learning based denoisers without ground truth data. arXiv preprint arXiv:1803.01314, 2018.
- Aja-Fernández S, Vegas-Sánchez-Ferrero G, Tristán-Vega A. Noise estimation in parallel MRI: GRAPPA and SENSE. Magnetic Resonance Imaging, 32(3):281–290, 2014.
- Pfaff L, Hossbach J, Preuhs E et al. Training a tunable, spatially adaptive denoiser without clean targets. In Proceedings of the joint annual meeting ISMRM-ESMRMB, 2022.
- Ramani S, Blu T, Unser M. Monte-Carlo SURE: A black-box optimization of regularization parameters for general denoising algorithms. IEEE Transactions on Image Processing, 17(9):1540–1554, 2008.
- Aubert-Broche B, Griffin M, Pike GB et al. Twenty new digital brain phantoms for creation of validation image data bases. IEEE Transactions on Medical Imaging, 25:1410–1416, 2006.
- Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 234–241, 2015.
- Zhang K, Zuo W, Chen Y et al. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising. IEEE Transactions on Image Processing, 26(7):3142-3155, 2017.
Figures

Table 1: Comparison between quantitative results
computed using MSE with ground truth and results computed using SURE without
ground truth averaged over a test set of 235 images.

Table 2: Comparison between quantitative results
computed using MSE with ground truth and results computed using SURE without
ground truth for a randomly selected image slice.
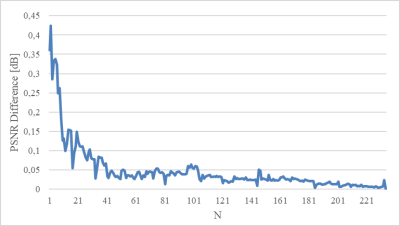
Figure 1:The absolute difference between the supervised
PSNR and the SURE-based PSNR averaged over N images.
DOI: https://doi.org/10.58530/2023/4046