Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence, Compressed sensing

We present a Bayesian optimization approach to find the optimal regularization parameters for undersampled MRI reconstructions such as Compressed Sensing (CS). Bayesian optimization can find optimal points for expensive to evaluate functions by efficient sampling the next points to try by maximizing the expected improvement. Additionally, the use of pruning can speed up optimization by stopping early unpromising trials. We demonstrate the effectiveness of this optimization technique by finding optimal parameters for undersampled MRI using Total Variation and CS-Wavelet regularization. The parameters found with the proposed approach are comparable to does found by grid search but requiring shorter computational times.

Introduction

A common approach for solving ill-posed inverse problems, such as undersampled MRI reconstruction from k-space measurements, is to iteratively solve a regularized optimization problem. These methods require setting the so-called regularization parameter, typically denoted by $$$\lambda$$$, that controls the balance between the data fidelity and priors imposed on the solution. This is especially challenging when there are multiple regularization parameters that need to be found. There is no current gold standard to select this parameter, and this is usually done by trial and error or using heuristic methods such as the L-curve. In this work, we propose the use of Bayesian optimization to find the optimal regularization parameter. Bayesian optimization has seen a lot of development in recent years^1,2 motivated by the need to find good hyperparameter for neural networks problems in the field of Automated Machine Learning (AutoML). These methods also known as black box optimizers, only require evaluating the function at arbitrary points and use a statistical model to determine which points to sample next.

Methods

If the true solution of a given inverse problem is known, it is possible to find the optimal regularization parameters by solving the following optimization problem
$$
\begin{align} \lambda_\text{opt} &= \arg\min D(\hat{x}(\lambda), x_\text{true}) \nonumber \\ \text{with}& \quad \hat{x}(\lambda) = \arg\min ||Ax - b||_2^2 + \sum_i \lambda_i\mathcal{R}_i(x)
\label{eq:opt}
\end{align}
$$
With $$$D(\hat{x}(\lambda), x_\text{true})$$$ a suitable distance measure between the reconstructed image and the ground truth. To solve the problem for undersampled MRI reconstruction we propose using Bayesian optimization. This method allows for efficient sampling of the next parameters to try by maximizing the expected improvement given the current data, balancing exploration and exploitation. Additionally, it is possible to use pruning to end a given trial if the current objective is performing worse than previous trials. This can drastically increase the optimization speed by not wasting resources on unpromising trials. Both ideas are implemented in the Optuna framework,³ originally develop for hyperparameter tuning in machine learning task. The proposed approach was applied to find the optimal regularization parameters $$$\lambda_\text{TV}$$$ and $$$\lambda_W$$$ for the following compressed sensing undersampled MRI reconstruction

\begin{equation} \min_x ||Ex - b||_2^2 + \lambda_\text{TV}\text{TV}(x) + \lambda_W||Wx||_1 \label{eq:CS}\end{equation}
where $$$E$$$ is the encoding matrix and $$$b$$$ are the k-space measurement. We used a 2D random Cartesian trajectory with under sampling factor of 2.32 and the “Split Bregman” algorithm to solve the reconstruction problem ref⁴ . Optuna was set up with default settings to find the optimal parameters and run 50 trials. The search space was set to $$$\lambda_W \in [1\times 10^{-12}, 1\times 10^{-1}]$$$ and $$$\lambda_\text{TV} \in [1\times 10^{-12}, 1\times 10^{-1}]$$$ in a logarithmic scale. The Structural Similarity Index (SSIM) in a region of interest (ROI) was used as the measure of reconstruction quality ($$$D$$$).

The proposed approach was tested on retrospectively undersampled cardiac CINE data for a single cardiac phase (from the OCMR dataset⁵. Parameters were optimized in one data set where fully-sampled reference is assumed to be known and same optimal parameters were used for other undersampled cardiac data sets. The proposed approach was compared against a grid search (GS) approach, where the reconstruction is solved for each combination (brute force approach), sampling points on a logarithmic grid in the same range used for Bayesian optimization.

Results

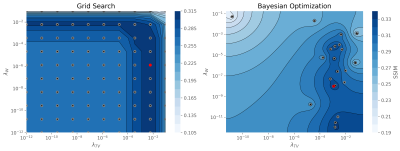
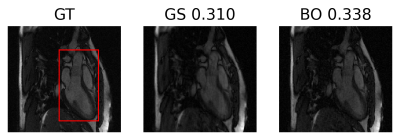
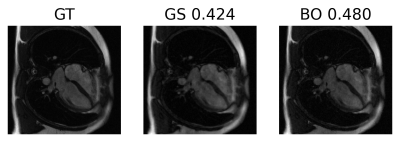
The optimal regularization parameters found with the proposed approach are shown in table 1 in comparison to the grid search method. Both methods found similar values, but Bayesian optimization takes almost half the time thanks to pruning, only needing to finish 21 trials. The optimization landscape for the proposed approach in comparison to the grid search method is shown in figure 2. It can be observed that the proposed approach identifies the ridge near $$$\lambda_\text{TV}=1\times 10^{-2}$$$. Also, we can see that Bayesian optimization only finish one trial for $$$\lambda_\text{TV}$$$ less than $$$1\times 10^{-4}$$$ where the grid search shows a suboptimal performance in this region.

Reconstruction results for the proposed approach (BO), grid search (GS) and the fully-sampled ground truth are shown in figure 3 for the case where the fully-sampled is considered to be known. Reconstructions using the same optimal parameters in a different data set (where fully-sampled data is not known) are shown in figure 4 showing good generalization of the found optimal parameters.

Conclusions and discussion

We show how Bayesian optimization can be used to find optimal regularization parameters for solving undersampled MRI reconstruction. The use of smart sampling and pruning can reduce optimization time by avoiding evaluating the function in points far from the optimal. Thanks to the advances in AutoML there are efficient implementation available that can be easily adapted for any optimization task.

Acknowledgements

A. D., C. P. and R. B. acknowledge support from ANID, Millennium Institute for Intelligent Healthcare Engineering (iHEALTH) ICN2021 004.