Synopsis

Keywords: Machine Learning/Artificial Intelligence, Motion Correction

Periodically Rotated Overlapping ParallEL Lines with Enhanced Reconstruction (PROPELLER) MRI technique enables the correction of motion artifacts resulted from patient motions in a scanner. Undersampling the blades can increase data acquisition speed and reduce potential motions caused by pains in a short time but may degrade image quality. Deep neural networks may support the blade reconstruction with undersampled data but motion patterns are difficult to be acquired for building a training dataset. To avoid the acquisition of training data, this abstract proposes an untrained neural network-based PROPELLER reconstruction technique to enhance image quality with undersampled blades.

Introduction

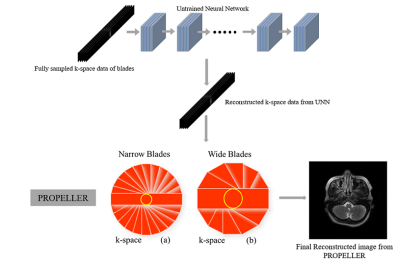
Periodically Rotated Overlapping ParallEL Lines with Enhanced Reconstruction (PROPELLER) MRI method can resolve the consequential issues of patient motion, for instance, artifacts due to motion and low resolution ¹. PROPELLER includes two stages: blade data acquisition and reconstruction stage. Data are collected in rotated k-space, containing N strips or blades ¹. Every strip of phase-encoded lines may typically be acquired in a number of ways, such as with a single stimulation RF pulse and several readouts ¹. The integration of k-space-based untrained neural network (UNN) prior in PROPELLER to reconstruct each blade can remove artifacts more precisely. As every single patient has a unique brain structure and motion patterns, reconstructing each strip from a trained neural network in the supervised learning mode may cause inaccurate results because training data are difficult to be acquired.

Methods

The proposed untrained neural network for PROPELLER is based on multi-coil k-space data, which can be expressed below
$$y = Ex + n$$
Here, $$$y$$$ is the undersampled k-space data of a blade, $$$x$$$ indicates a blade image to be reconstructed, $$$n$$$ is noise, and $$$E$$$ is an encoding matrix for each blade. For example, the encoding matrix can be the sensitivity encoding (SENSE) with a PROPELLER trajectory ⁶. To solve this inverse problem and avoid the acquisition of training data, we use UNN ² for recovering $$$x$$$. The flowchart of the proposed method is illustrated in Figure 1. UNN is used to reconstruct all blade images.

We used different brain slices extracted from two volunteers to test the proposed method. The tested brain slices were fully sampled k-space data obtained from a 3T Philips Ingenia scanner. Each four-dimensional slice contains 24 blades or strips, 13 coils, and a 30×436 field-of-view (FOV) of a blade. For sampling trajectories, different 1D cartesian sampling trajectories were applied. In the center of the k-space, there were 8 auto-calibration signal (ACS) lines for each undersampling in the phase-encoded direction. We initialized the parameters as ADAM optimizers ³ in UNN, $$$ \beta_A = 0.9 $$$, $$$ \beta_B = 0.999 $$$ , total iterations 1000, and the learning rate as 10^-4. The proposed method implementation was performed using PyTorch and GPILAB ⁷ in a machine with windows 10 operating system, NVIDIA Quadro P2200 GPU, INTEL Core i7 processor, and 64 GB memory.

Two volunteer datasets were acquired on a Philips Ingenia 3T scanner with a 13-channel head phased-array coil. A TSE PROPELLER sequence is used for acquiring data (repetition time [TR]/echo time = 4000/109 ms; ETL = 30; matrix size = 436 x 436; slice thickness = 4 mm; 24 slices; FOV = 25 cm). Informed consent was obtained from all volunteers for all in vivo experiments in accordance with institutional review board policy. All coils of each corresponding blade are combined using the square-root of sum of squares, $$$ s[n] = ( \sum_{k=1}^{n} | x_k [n]|^2 )^ \frac{1}{2} $$$ , before inserting it into the PROPELLER. Then, the motion correction is gained through several stages, including phase correction, correcting rotation, translation adjustment, and correlation weight ¹.

Results

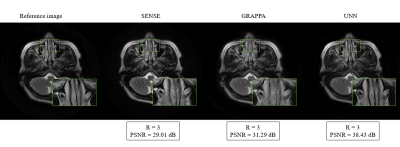
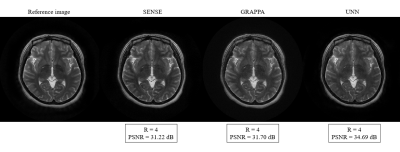
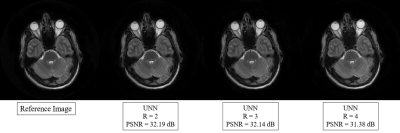
To evaluate the proposed method's performance, we compared it with the two most widely used parallel imaging methods for PROPELLER trajectories, SENSE ⁴ and GRAPPA ⁵. We used the same parameters and same calibration for all methods, where we applied the same undersampling trajectories with a reduction factor. Figure 2 shows that the proposed method outperforms the other two methods using the reduction factor R = 3 and 8 ACS lines. Moreover, we also investigated the performance using different ACS in the phase encoding direction. For quantitative comparison, we calculated the peak-signal-to-noise ratio (PSNR) for each brain slice reconstructed from these three methods in the image domain, as shown in Figure 3. Our proposed method was able to gain superior performance in every single case in terms of quantitative performance and visual image quality. However, when the number of acquired lines or ACS was less, PROPELLER SENSE and PROPELLER GRAPPA suffered a loss of image quality with a significant amount of noise and artifacts. On the other hand, our proposed method exhibits substantial performance improvement compared to PROPELLER SENSE and PROPELLER GRAPPA when there was less calibration region. Figure 4 shows the PROPELLER UNN reconstruction results for R=2, 3, and 4. PSNR value decreases along the R increases.

Discussion and Conclusion

In this work, we proposed a UNN prior to improve PROPELLER imaging quality in the k-space domain, which enhances the process of motion correction more precisely. This is the first method to use UNN prior in the PROPELLER MRI, which provides a larger variety of applications in addition to better prior characterization. No training data are required by using neural network methods. Our method outperforms the traditional SENSE-based and GRAPPA-based PROPELLER methods in terms of reconstruction accuracy. Thus, using a pre-trained neural network via external training data for reconstructing each strip is not a feasible approach, as brain strips can have a different structure for every individual, and each patient’s motion patterns are deviated.

Acknowledgements

No acknowledgement found.