Synopsis

Keywords: Machine Learning/Artificial Intelligence, Machine Learning/Artificial Intelligence

Various image reconstruction methods have been proposed to reduce Magnetic resonance (MR) image acquisition time. One of recent trends is convolution neuron network (CNN) based deep learning model. However, most of these CNN models keep architecture of stacking small filters (e.g. 1×1 or 3×3) and the effective receptive field of these networks is limited, which is undesired for reconstruction because the random undersampling pattern causes global artifact. We proposed Fourier convolution block (FCB) to replace regular convolution filters. FCB can achieve both global receptive field and high computing efficiency by multiplication in frequency domain.

Introduction

Convolution neuron network (CNN) based deep learning model has delivered remarkable performance in magnetic resonance imaging (MRI) reconstruction in recent years. The state-of-the-art methods such as Unet¹ and unroll model² achieve good results. However, recent researches^3,4 claim that the effective receptive field of current CNN model with 3×3 convolution kernels is still limited despite their cascade structure and pooling layer. Specifically, the artifact of random undersampled images are global, and the above methods, with a limited receptive field, is ineffective to learn details.
Fourier convolution is firstly proposed to accelerate computation of regular convolution⁵ and regraded as a global operation to enlarge the receptive field of token mixer⁶. Some CNN models in frequency domain^7,8 have been proposed to benefit from global information, but their method is convolution between different frequencies. Instead, Fourier convolution is an equivalence of spatial convolution, and it could cover large receptive field while keeping characteristic feature of convolution. It has not been studied in the field of magnetic resonance reconstruction.
In this work, we propose the Fourier Convolution Block (FCB) as a generic enhancement for existing CNN models for MRI reconstruction. The proposed method is tested in retrospective MR knee data in end-to end model and unroll model and we show that the valid receptive field is really enlarged by visualizing kernel in frequency domain.

Methods

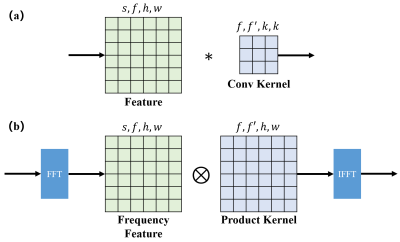
Theory: The proposed FCB is shown in Fig 1, which is an equivalent in Fourier domain of regular convolution. The production kernel of FCB has the same size with input feature map, and it could correspond to any spatial convolution kernel with arbitrary size between 1 to input size.
$$\begin{equation}w * x = \mathcal{F}^{-1}[ \mathcal{F}{(w)} \otimes \mathcal{F}{(x)}] \tag{1}\end{equation}$$In other words, the equation (1) is valid for the weight $$$w$$$ with any size less than the size of input $$$x$$$. This character makes possible a global receptive field and ability to learning kernel size. In the meantime, FCB has less computational complexity compared with regular convolution. If the input size is $$$(s,f,h,w)$$$, correspond to (batch size,input channels,height,weight), regular convolution with kernel size have a complexity of $$$O(f×f'×h×w×k×k)$$$. However, FCB’s complexity is $$$O(f×f'×h×w)$$$ when the complexity of FFT is relatively negligible.
Architecture: We verify FCB in two popular DL based MRI reconstruction model: end to end UNet and unroll model with resblocks. To decrease the parameters of network, the most of convolution layers are designed as a depth separable form. What’s more, for UNet, we modify its “double convolution” as the structure in ⁹. The padding mode of convolution is circular-padding rather than zero-padding to ensure the equivalence between FCB and spatial convolution.
Training setting: For both UNet and unroll model, Adam optimizer is utilized with 1e-4 learning rate and none of regularization is used. All models are trained with L1 loss function, and the metric for model selection is NMSE. For UNet, the channel of first hidden layers is 64 and down sampling executes 4 times. For unroll model, number of resblocks is 2 and number of iteration is 8. Models with FCB are trained by a structural re-parameterization approach to ensure better convergence.
Data setting: Fully sampled PD weighted 2D knee data in FastMRI¹⁰ is used. The images are crop to 320×320 and Cartesian undersampling pattern is used to generate data retrospectively. Each volume is normalized to 0-1. We choose the data without fat suppression due to their better SNR. We use the 2963 slices from 100 volunteers for training and 524 slices from 18 volunteers for validation and the validation set is regarded as test set.

Resuts

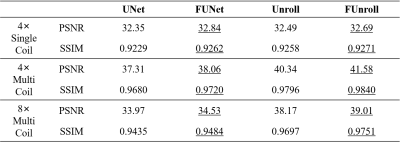
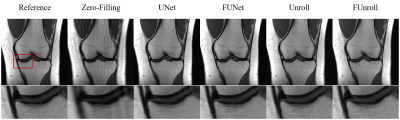
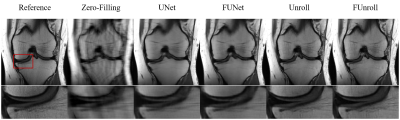
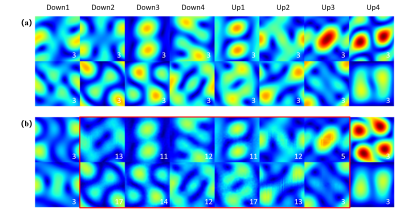
All the quantitative results are shown in Table 1. FCB could improve model’s performance in single-coil and multi-coil data at 4× and 8× acceleration. In particular, the proposed method can get the better numerical results for unroll model in high reduction factor, which indicates that the proposed method have strong robustness. Figure 2 shows the reconstructed result of multi-coil data at 4× acceleration from baseline model and its variant with FCB. The proposed method has the best reconstruction of the meniscus in the unroll model as shown in the red box. Figure 3 shows results at 8× acceleration. It can be seen that the proposed method still has better image reconstruction results under high reduction factor. UNet has a heavy smoothing effect on images and FCB helps to recovery details. For Unroll model, FCB version behaves well in the texture and detail of skeleton and cartilage. Besides, we visualize the trained production kernel in frequency domain as shown in Figure 4. Because Fourier transform is orthogonal, the rank of kernel is constant between frequency domain and spatial domain. The trained kernels have the rank larger than the fixed value of CNN model, which corresponds to large spatial filter with large receptive field.

Discussions ＆ Conclusion

The proposed FCB, as a simple replacement for regular convolution, could effectively enlarge the receptive field of model while adaptively learning the kernel size of spatial filter. It achieves better PSNR and recovery in details on knee data in different accelerations. However, its utility should be fully explored for more strictly controlled experiments.

Acknowledgements

No acknowledgement found.