3971
The Trouble with Free-Water Elimination using Single-Shell Diffusion MRI Data: A Case-Study in Ageing1MRC Cognition and Brain Sciences Unit, University of Cambridge, Cambridge, United Kingdom, 2BioMedIA Group, Department of Computing, Imperial College London, London, United Kingdom, 3Division of Anaesthesia, Department of Medicine, University of Cambridge, Cambridge, United Kingdom, 4Institute for Systems and Robotics - Lisboa and Department of Bioengineering, Instituto Superior Técnico, Universidade de Lisboa, Lisbon, Portugal
Synopsis
Keywords: Data Analysis, Diffusion/other diffusion imaging techniques, Ageing, Free-Water
Two different algorithms for free-water elimination (FWE) were applied to single-shell and multi-shell diffusion MRI data. Positive correlations were found between age and fractional anisotropy (FA) estimated with the FWE algorithm for single-shell, but this was not replicated with multi-shell diffusion data. Because only the multi-shell FWE algorithm is well-posed, we postulated that the positive correlations between age and FA must be a false positive finding, resulting from inappropriate fitting using single-shell data. FWE estimates from single-shell modelling have been shown to be biologically plausible, but this does not imply specificity, and more work is required to validate these approaches.
Introduction
The Free-water elimination (FWE) model for Diffusion Tensor Imaging (DTI) was first introduced by Pierpaoli1. Besides estimating the volume fraction of FW (FW index), this model can also estimate FW-compensated DTI parameters. Single-shell (SS) diffusion MRI acquisitions are more common in clinical cohorts due to time constraints. However, the FWE-DTI model is a two-compartment model, hence only well-posed for multi-shell (MS) data. To overcome this constraint, Pasternak2 proposed a spatially regularized gradient descent (RGD) algorithm to fit the FWE-DTI model to single-shell data, which is highly dependent on the initialisation method3. This regularised approach has been used to study healthy ageing4, Alzheimer’s5 and Parkinson’s6 disease, amongst others, largely ignoring the methodological concerns over RGD procedures.Here, we compared the performance of RGD fitting with SS data, to a non-linear least squares (NLS) fitting applied to MS data, using 620 datasets from the CamCAN project7. Our aim was to determine whether both methods lead to comparable research findings.
Methods
MRI data from 620 healthy adults (age range: 18-88 years, 315 females) were included in this study. Diffusion data were collected along 30 gradient directions for two b-values (1000 and 2000 s/mm2), plus three b=0 images. Other acquisition parameters were: TR=9100ms, TE=104ms, voxel size=2mm isotropic, FOV=192mm × 192mm, and 66 axial slices, total acquisition time of 10 minutes and 2 seconds.The data were de-noised8 and corrected for Gibbs ringing9, eddy currents, head movement artefacts10 and signal inhomogeneities using DIPY11. DTI modelling was performed using weighted-linear least squares fitting in FSL12. DTI fitting was applied to the full dataset (DTI MS), and then repeated by excluding the b=2000s/mm2 data (DTI SS). This was done to assess the potential effects of non-Gaussian diffusion introduced by the b=2000s/mm2 data. In both cases, mean diffusivity (MD) and fractional anisotropy (FA) maps were generated. FWE was performed in two ways: firstly, the full dataset was used to estimate FWE-DTI parameters using MS NLS fitting; secondly, the b=2000s/mm2 data were excluded and the remaining data used to estimate FWE-DTI parameters with RGD for SS data. Both SS and MS FWE-DTI fitting were performed using the procedures implemented by Golub3 in DIPY. In total we generated 10 whole-brain maps of diffusion metrics for each volunteer: dti_FA_SS, dti_FA_MS, dti_MD_SS, dti_MD_MS, fw_FA_SS, fw_FA_MS, fw_MD_SS, FW_index_SS, fw_MD_MS, and FW_index_MS.
Standard TBSS13 was applied to the dti_FA_SS data. The tbss_non_FA script was then applied to the other maps to generate skeletonised data for all 10 metrics. FSL’s randomise with 5000 permutations was used to identify which skeleton voxels correlate with age for each metric, using TFCE for correction for multiple comparisons. Significant correlation between age and diffusion metrics was defined by a corrected p-value < 0.01.
Results
As previously reported4, we found positive and widespread correlations between MD and age, for all combinations of model fitting and dataset (Figure 1). When FWE is performed, the number of significant voxels decreases and this effect is more pronounced for the RGD method (Figure 2B). The FW index also shows widespread negative correlations with age, for both the RGD and NLS algorithms (Figure 1), but more significant voxels were identified with the RGD approach (Figure 2C). Both DTI-based FA metrics produced similar results, showing strong negative correlations with age across the whole brain. However, FW compensated FA maps produced strikingly different results depending on the method employed: the maps obtained with RGD SS identified some brain areas with a strong positive association with age – contrasting the known prevalence of FA decline with age14 – while no such positive correlations were found with MS NLS (Figure 1).Discussion
For the standard DTI model the results were similar for MS and SS data. However, the maps obtained with MS data resulted in larger number of significant voxels for both MD and FA, suggesting non-Gaussian effects introduced by the b=2000s/mm2 can lead to false positive findings. This is in line with previous studies(e.g.,15) showing DTI is not appropriate for b-values greater than 1500s/mm2.Our results suggest the RGD algorithm can lead to erroneous findings. Similar positive correlations between age and FW-compensated FA maps obtained with SS RGD have been reported4, which were interpreted as related to selective degeneration of non-dominant tracts at fibre crossings. However the replication of these observations when the RGD SS was used, but not with the well-posed MS method, suggests this apparent FA increase was merely an artefact introduced by inappropriate modelling using SS data.
Although MS NLS fitting is undoubtedly more accurate than RGD on SS data, we cannot ignore that our MS FW estimates will be affected by non-Gaussian effects from the b=2000s/mm2 data. Previous work16 has shown that using high b-values to model FW in MS diffusion data leads to increased FW estimates, but the impact on FA was not characterised. Therefore further work is required to ensure non-Gaussian effects cannot explain the discrepancies observed for the FW-compensated FA maps.
Conclusion
Findings using FW-compensated DTI maps depend heavily on the fitting method. More work is needed to validate the RGD approach using SS data, and the findings reported in the literature using such methods should be interpreted with extreme care.Acknowledgements
This work was supported by the Medical Research Council (SUAG/109 G116768) and Fundação para a Ciência e a Tecnologia (UID/EEA/50009/2019 and UID/EEA/50009/2020).References
1. Pierpaoli C, Jones DK. Removing CSF contamination in brain DT-MRIs by using a two-compartment tensor model. In: Proc 12th Annual Meeting ISMRM, Kyoto; 2004: 1215.
2. Pasternak O, Sochen N, Gur Y, Intrator N, Assaf Y. Free water elimination and mapping from diffusion MRI. Magn Reson Med 2009;62:717-730.
3. Golub M, Neto Henriques R, Nunes RG. Free-water DTI estimates from single b-value data might seem plausible but must be interpreted with care. Magn Reson Med. 2021; 85:2537-2551.
4. Cha JA, Pasternak O, Salat DH, Jean Chen J. Re-examining age-related differences in white matter microstructure with free-water corrected diffusion tensor imaging. Neurobiology of Aging 2018; 71: 161-170.
5. Hoy AR, Ly M, Carlsson CM, et al. Microstructural white matter al-terations in preclinical Alzheimer’s disease detected using free water elimination diffusion tensor imaging. PLoS One. 2017; 12:e0173982.
6. Planetta PJ, Ofori E, Pasternak O, et al. Free-water imaging in Parkinson’s disease and atypical parkinsonism. Brain. 2016; 139:495-508.
7. Shafto MA, Tyler LK, Dixon M, Taylor JR, Rowe JB, Cusack R, Calder AJ, Marslen-Wilson WD, Duncan J, Dalgleish T, Henson RN, Brayne C, Cam-CAN, & Matthews FE. The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) study protocol: a cross-sectional, lifespan, multidisciplinary examination of healthy cognitive ageing. BMC Neurology 2014; 14:204.
8. Veraart J, Fieremans E, and Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med 2016; 76(5): 1582-1593.
9. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs‐ringing artifact removal based on local subvoxel‐shifts. Magn Reson Med 2016; 76(5): 1574-1581.
10. Andersson JLR and Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 2016; 125: 1063-1078.
11. Garyfallidis E, Brett M, Amirbekian B, Rokem A, van der Walt S, Descoteaux M, Nimmo-Smith I, and Dipy Contributors. Frontiers in Neuroinformatics 2014; 8:8.
12. Smith, Jenkinson, Woolrich, Beckmann, Behrens, Johansen-Berg, Bannister, De Luca, Drobnjak, Flitney, Niazy, Saunders, Vickers, Zhang, De Stefano, Brady, Matthews Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004; 23: 208-219.
13. SmithSM, Jenkinson, Johansen-Berg, Rueckert, Nichols, Mackay, Watkins, Ciccarelli, Zaheer Cader, Matthews, BehrensTract-based spatial statistics: voxelwise analysis of multi-subject diffusion data 2006; 31(4):1487-505.
14. Sullivan EV, Adalsteinsson E, Hedehus M, Ju C, Moseley M, Lim KO, Pfefferbaum A. Equivalent disruption of regional white matter microstructure in ageing healthy men and women. Neuroreport 2001; 12(1): 99–104.
15. Jones DK, Basser PJ. “Squashing peanuts and smashing pumpkins”: How noise distorts diffusion-weighted MR data. Magn Reson Med. 2004; 52(5):979-993.
16. Neto Henriques, R. Advanced Methods for Diffusion MRI Data Analysis and their Application to the Healthy Ageing Brain. Diss. University of Cambridge, 2018.
Figures
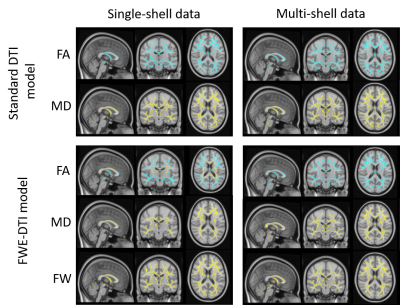
Figure 1 – The effect of FWE elimination on DTI metrics. The results for MD and FW index are consistent for both FWE algorithms, showing widespread negative correlations with age (in blue). However, the FW-compensated FA maps obtained with single-shell FWE modelling resulted in positive correlations with age in some brain regions (in yellow), which could not be replicated when the multi-shell FWE model was used. These were also not present for standard DTI FA maps.
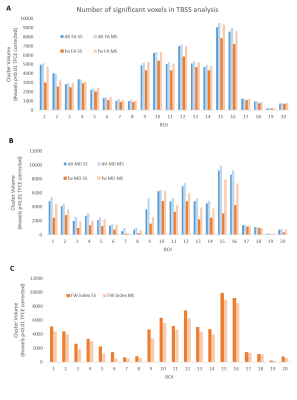
Figure 2 – Number of significant voxels in TBSS analysis for (A) FA maps, (B) MD maps and (C) FW index, per ROI in the JHU white-matter tractography atlas. ROI labels can be found in Figure 3. For FA and MD the number of significant voxels decreased when FWE was applied, but to a lesser degree for MS NLS fitting. For the FW index the opposite trend was observed and there were fewer significant voxels when MS NLS was applied.
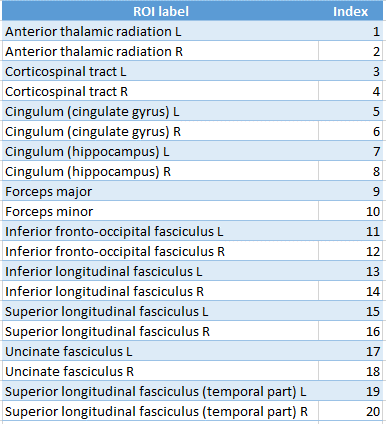
Figure 3 – ROI labels for the JHU white-matter tractography atlas.