Synopsis

Keywords: Artifacts, Diffusion/other diffusion imaging techniques

Diffusion weighted images are usually acquired using 2D EPI methods. This technique has the limitation of low spatial resolution and low SNR. 3D diffusion weighted images are attractive option for improved SNR, however the motion-induced phase inconsistencies pose a challenge for the reconstruction of such data. We present a navigator-free phase-compensated reconstruction, which can be implemented as a regular parallel imaging framework. This two-step method involves first estimating a low-resolution phase from the data itself and then integrating the phase information in the forward encoding operator. We show good phase compensation from accelerated datasets using the proposed approach.

Introduction

High Resolution Diffusion MRI (dMRI) enables the study of tissue microstructural features in detail, enabling better understanding of neurological disorders. Unfortunately, as the voxel sizes are reduced, the affordable resolution is limited by the SNR available from the reduced excitation volume. 3-D excitation is an alternative strategy to improve the SNR. In combination with 3D Fourier encoding along the z-direction, very thin slices can be achieved with good SNR^1-4. However, this method suffers from several inefficiencies. The typical 3D multi-slab DWI (3DMS-DWI) images are acquired using a multi-shot read-out, with one k_z encode per TR. This leads to (i) sensitivity to phase inconsistencies arising from motion between shots, and (ii) increased scan time, making it further vulnerable to motion artifacts.

Methods

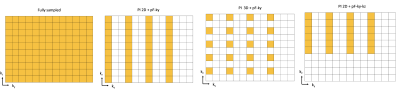
To reduce scan time, here we test under-sampled 3DMS-DWI acquisitions in the context of dMRI. While such under-sampling schemes were previously studied in the context of whole-brain 3D EPI^5-6 , its extension to 3DMS-DWI is non-trivial due to the phase inconsistencies. Moreover, previous 3DMS-DWI techniques relied on a navigator-based approach to correct for the phase inconsistencies. In this work, we extend the previously proposed navigator-free reconstruction approach⁷ for the phase corrected reconstruction of accelerated 3DMS-DWI acquisitions.

Figure 1 shows the various sampling patterns used in this study. Table 1 lists the scan time associated with each sampling pattern. For the accelerated phase-compensated DWI reconstruction, we re-formulated the navigator-free approach in [7] as a generalized SENSE reconstruction problem⁸.
$$
\tilde{\mathbf S} = argmin_{\mathbf S} ||\mathcal {A}(\mathbf S)-\widehat{\mathbf Y }||_2^2 + \lambda_1 || \mathbf S||_{TV},
$$
where $$$\mathbf S$$$ is the 3D DWI of size N_x x N_y x N_z and $$$\widehat{\mathbf Y }$$$ is the measured multi-channel k-space data. The reconstruction of the under-sampled data is initialized using a zero-filled input to the desired size. $$$\mathcal {A}({\mathbf S})$$$ is a SENSE-based forward operator composed of $$$\mathcal{M}∘ F ∘CS $$$. Here, the DWI $$$\mathbf S$$$ is weighted by the composite sensitivities $$$CS$$$ followed by 3D Fourier transform $$$ F $$$ and multiplication by a sampling mask $$$\mathcal{M}$$$. The phase for each kz encode is estimated before-hand from the accelerated data itself using a parallel-imaging extension of [7]. A total variation regularization is added to improve the conditioning of the above reconstruction.

We also tested a second reconstruction, the qModeL⁹, for the phase correction of the accelerated 3DMS-DWI acquisitions. The associated reconstruction is a modification of the generalized SENSE reconstruction given above with an additional plug-and-play denoiser $$$\mathcal P_{\Theta}(\mathbf S)$$$ and is given by
$$\tilde{\mathbf S} = argmin_{\mathbf S} ||\mathcal {A}(\mathbf S)-\widehat{\mathbf Y }||_2^2 + \lambda_1 || \mathbf S||_{TV} + \lambda_2 ~ ||\mathcal P_{\Theta}(\mathbf S) ||_2^2.$$

In-vivo experiments were performed using a custom 3DMS-DWI sequence developed using the KS Foundation base sequences^10-11. Data was collected on a GE 3T Premier scanner (G_max 80mT/m, 200 mT/m/ms, 48-channel receive coil). A 1mm isotropic resolution dataset was collected as follows: a 3-shot acquisition was used, which segments the ky readout into 3 interleaved acquisitions with a partial Fourier (pF) factor of .6 in the ky direction. To achieve whole-brain coverage, ten slabs, each of 10 mm thickness, were prescribed with 10 kz encodings (oversampling by 20% and a slab overlap of 1mm). No navigators were used. More details are given in Table 1. For comparison, a 2D single-shot DWI EPI scan was also collected with matched resolution and b-weighting and NEX of 4. No multi-band acceleration was used.

To test the feasibility of accelerated 3DMS-DWI routine experiments, we also collected a second dataset with 30 directions resulting in a lengthy scan (15 mins) during which motion is inevitable resulting in phase inconsistencies. This dataset was collected with modified CAIPI-like under-sampling scheme. Both reconstructions were tested on this dataset for studying their effectiveness in removing the phase artifacts.

Results

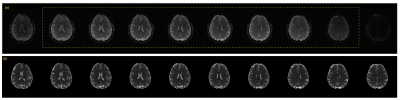
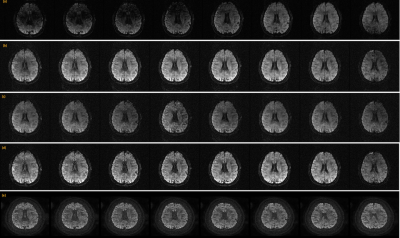
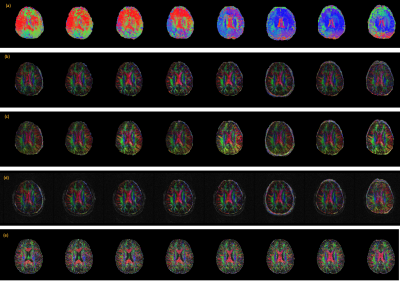
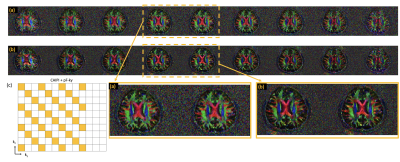
Figure 2 shows the reconstruction of the b0 images from a given slab and its comparison to a standard 2D case. Figure 3 shows the reconstruction of the DWIs for the various under-sampling patterns using the proposed method and its comparison to the 2D case. A SENSE reconstruction with no phase compensation is also shown for comparison.

Figure 4 shows the color-coded fractional anisotropy maps computed from the 6-direction dataset. Clearly any residual phase inconsistency will result in a modified color map. Figure 5 shows the color-coded fractional anisotropy maps computed from the 30 direction dataset using the qModeL method and the generalized SENSE method and well as the sampling pattern used.

Discussion and Conclusion

Figures 3-4 show effective phase correction accomplished using the proposed formulation for the accelerated cases. Figure 5 shows the effectiveness of the proposed method for routine longer acquisitions. Together these experiments show that the 3D under-sampled acquisitions can be reconstructed without phase artifacts from navigator-free acquisitions. Moreover, we also tested the feasibility of various under-sampling schemes for acceleration of the 3DMS-DWI scans. In particular, the partial Fourier applied along both ky and kz shows promising performance as expected.

In conclusion, 3DMS-DWI has the potential to provide high resolution images with good SNR enabling imaging of microstructural features in great detail. Future works will combine the slab profile artifact correction methods with the above accelerated reconstruction.

Acknowledgements

The developments were supported by NIH grants 1R01EB031169, and 1S10OD025025-01