3963
Robust Complex Signal Averaging for Diffusion Weighted Imaging
Xinzeng Wang1, Daniel Litwiller2, Arnaud Guidon3, Patricia Lan4, and Tim Sprenger5
1GE Healthcare, Houston, TX, United States, 2GE Healthcare, Denver, CO, United States, 3GE Healthcare, Boston, MA, United States, 4GE Healthcare, Menlo Park, CA, United States, 5GE Healthcare, Stockholm, Sweden
1GE Healthcare, Houston, TX, United States, 2GE Healthcare, Denver, CO, United States, 3GE Healthcare, Boston, MA, United States, 4GE Healthcare, Menlo Park, CA, United States, 5GE Healthcare, Stockholm, Sweden
Synopsis
Keywords: Data Processing, Diffusion/other diffusion imaging techniques
In the past decade, complex signal averaging has been investigated for diffusion weighted imaging to address the well-known noise floor issue. The robustness of complex signal averaging highly depends on the performance of phase correction to remove the shot-to-shot background phase variations. To achieve optimal phase correction, parameters (kernel size, regularization terms, etc.) need to be tuned for different anatomies, SNR levels and/or image size. In this work, we evaluated a deep-learning based phase correction method for various DWI applications, including brain, liver, prostate and showed improved complex signal averaging with lower noise floor and less artifacts.Introduction
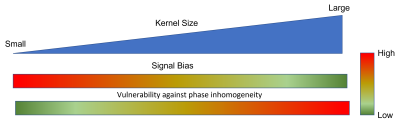
Signal averaging is a common method to increase signal to noise ratio (SNR) in diffusion weighted imaging (DWI). DW image is inherently complex-valued, and motion, eddy current, etc. could cause shot-to-shot background phase variations. To eliminate the impact of shot-to-shot phase variations, magnitude-based signal averaging is widely used in DWI. However, the traditional magnitude-based averaging suffers from the well-known noise floor issue, leading to biased estimation of diffusion parameters. Complex signal averaging could reduce the noise floor but requires phase correction prior to signal averaging.In the past decade, various phase estimation/correction methods have been proposed and investigated for complex signal averaging in DWI [1-3]. In general, there are two principal methods, low-pass filter based and total-variation based phase estimation. Filter-based background phase estimation is simple and fast, but the kernel size requires tuning to balance signal bias and high-frequency spatial information. As illustrated in Figure 1, increasing the kernel size reduces signal bias, but leaves behind more high spatial frequency information in the imaginary image. [1] Total variation method could preserve shape edges in the phase map but is more compute intensive. Moreover, both methods require parameter tuning (kernel size, TV regularization, etc.) based on experience to achieve optimal performance when the anatomy, inherent SNR, image size, etc. are changed. This reduces the robustness and generalization of these phase correction methods.
In this study, we aimed to evaluate a deep-learning based phase correction method to improve the robustness and performance of complex signal averaging in various DWI applications, including body and neural DWI.
Methods
To evaluate and compare different phase estimation/correction methods, brain and liver DW images were acquired on a GE 3T MRI scanner (Discovery MR750, GE Healthcare, Waukesha, WI) with IRB approval and written informed consent.Brain DWI images were acquired at b=2500 and 8000 s/mm2 to evaluate the performance of phase correction at the different SNR levels. Liver DWI images were acquired at b=1000 s/mm2 to evaluate the performance of phase correction with large background phase variations, which could be introduced by multiple sources including cardiac, respiratory motion, etc.
For filter-based phase estimation, Fermi filters with different radii (r = 16, 36) were applied in the k-space domain. Note that a Fermi filter with larger radius in k-space domain corresponds to a smaller kernel in image domain.
For DL-based phase estimation, a deep-learning based network was trained from a database of over 10,000 images with various SNR levels and background phases. Both methods were embedded in the conventional reconstruction pipeline to generate two sets of image series (Filter-based phase corrected and DL-based phase corrected images) from the same set of raw MR data.
Results and Discussion
Figure 2 shows the brain DW images at b=2500. Phase correction with a large kernel (Fermi16) minimized the signal bias and reduced background noise in the averaged image, but left more signal in the imaginary channel (Figure 2g). Reducing the kernel size (Fermi36) reduced the signal in the imaginary channel but resulted in increased signal bias and higher noise floor (Figure 2e). DL-based phase correction achieved minimal signal bias and noise floor while preserving signal in the real channel (Figure 2f, 2i).DL-based phase correction also achieved similar performance in extreme low SNR images. The single NEX image at b=8000 is very noisy. It is challenging to distinguish high-frequency background phase from noise using conventional denoising method. With DL-based phase correction, the imaginary channels for both single and multi-NEX images are mainly dominated by noise and there is no signal left in the imaginary channel after phase correction. This indicated that DL-based method achieved robust phase correction at extreme low SNR.
In the liver DWI, both low-frequency phases and high frequency phases (in red contour) were present in single shot DW image, as shown in Figure 4a. Conventional magnitude averaging (Figure 4e) was used to eliminate the impact of these background phases, but suffered from high noise floor, as shown in Figure 4i. Smoothing kernels could be applied to estimate the background phases for complex averaging. However, a large smoothing kernel generated an over-smoothed phase and lost high-frequency spatial information (Figure 4b), resulting in shading artifacts in the averaged image (Figure 4f). In contrast, a small smoothing kernel minimized the smoothing (Figure 4c) and shading artifacts (Figure 4g) but increased signal bias, resulting in a higher noise floor (Figure 4k). Deep learning based phase correction could more accurately correct both high frequency and low frequency phases in tissues (Figure 4d), eliminating shading artifacts (Figure 4h) while minimizing noise floor in the averaged image (Figure 4l).
Conclusion
The deep-learning based phase correction method could effectively remove both high-frequency and low-frequency background phase while minimizing signal bias and maintaining Gaussian noise distribution. Improved robustness and performance of complex signal averaging was demonstrated in various DWI applications, including body and neural DWI.Acknowledgements
No acknowledgement found.References
[1] Douglas E Prah, etl. Magn Reson Med. 2010 Aug; 64(2): 418–429
[2] Eichner Cornelius, etl. Neuroimage. 2015 Nov 15; 122: 373-384
[3] Tim Sprenger, etl. Magn Reason Med. 2017 Feb;77(2):559-570
Figures
Figure
1. In filter-based phase correction, larger kernel size in the image domain
could reduce the signal bias and maintain Gaussian noise distribution, but more
high-frequency signal will be left in the imaginary channel, resulting in loss
of signal.
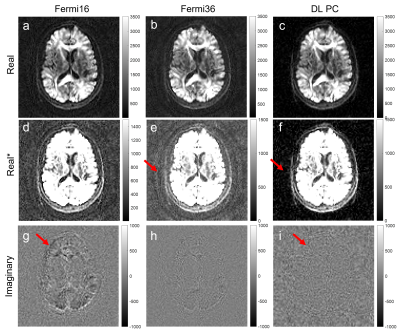
Figure 2. Complex averaging using
filter-based phase correction and DL-based phase correction with b=2500 brain
images. (a-c) are the real images; (d-f) are the same images but with a
different window level to show the background noise; (g-i) are the imaginary
images. Compared to a small kernel (Fermi36), a large kernel (Fermi16) could
reduce the signal bias, resulting in a lower noise floor (d vs e). However,
more signal was also left in the imaginary channel (g vs h). In contrast, DL-based phase correction showed
lowest noise floor and minimum loss of signals.
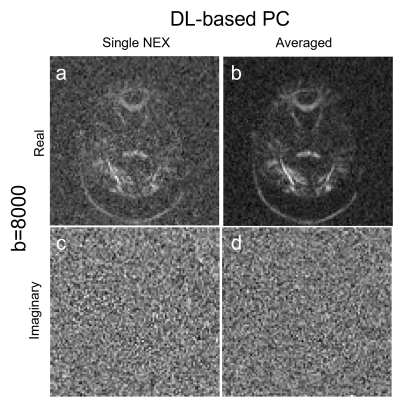
Figure 3. Complex averaging using DL-based phase correction
with b=8000 brain images. (a-b) are the real images; (c-d) are the imaginary
images. DL-based phase correction showed robust phase correction without noticeable
signal loss at extreme low SNR.

Figure 4. Liver DWI images (b=1000). (a-d) are the phase maps pre-/post- phase
correction; (e-l) are the magnitude and complex averaged images with different
window levels. Body DWI often uses magnitude averaging and shows high noise
floor (i) and complex averaging is challenging due to large phase variations
(a). Compared to a large kernel, small kernel could capture some high-frequency
phases and reduce banding artifacts (g vs f), but still fails in some regions and increases the noise floor (k vs j). DL-based phase correction showed lowest
noise floor and banding artifacts.
DOI: https://doi.org/10.58530/2023/3963