3960
Extended multi-shell diffusion acceleration with Gaussian processes estimated reconstruction (ems-DAGER)1Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, UK, Oxford, United Kingdom
Synopsis
Keywords: Image Reconstruction, Diffusion/other diffusion imaging techniques, Signal modelling
Diffusion-weighted MRI suffers from relatively long acquisition time, especially for high spatial- resolution and/or high angular- resolution acquisitions. Thus, methods to increase the acquisition speed are urgently needed. Recently, increasing attention has been paid to utilize the relations between k- and q-space points for further acceleration. Here, we extend the Diffusion Acceleration with Gaussian process Estimated Reconstruction (DAGER) to leverage shared information in multi-shell acquisitions and incorporate eddy-induced distortion correction.Introduction
High spatial- and angular- resolution dMRI can benefit neuroscience with more accurate characterization of tissue properties at the cost of longer scan times1-2. A range of methods to accelerate dMRI acquisition have been proposed including traditional k-space acceleration3-5, q-space acceleration6-7 and joint k-q acceleration methods8-10. Diffusion Acceleration with Gaussian process Estimated Reconstruction (DAGER)11 achieves highly accelerated dMRI by exploiting q-space smoothness with Gaussian processes12 to inform undersampled k-space reconstruction.Currently, DAGER has two major limitations. First, it can only reconstruct single-shell dMRI data, which is not compatible with advanced biophysical models13-14. Second, to minimize the impact of eddy current distortions, antipodal symmetric property of q-space signal has not been utilized, which limits the potential of DAGER for achieving higher accelerations. In this work, we extend DAGER for multi-shell acquisition (ems-DAGER) and incorporate eddy-current distortion correction into a joint k-q reconstruction. We demonstrate improvements of ems-DAGER for multi-shell data using highly-realistic simulations.
Method
Multi-shell DAGERDAGER uses Gaussian Processes (GP) to model dMRI signals15. For single-shell dMRI data, the covariance of signals on the q sphere is characterised using a spherical covariance function :
$$c(x,x′)=C_\theta (arccos|⟨g,g′⟩|;a) (1)$$
with
$$C(\theta)=\begin{array}{l} \\ \left\{\begin{matrix} 1-\frac{3\theta }{2a} +\frac{\theta ^{3} }{2a^{3} } \ \theta < a\\ 0\ \theta \ge a\end{matrix}\right. \end{array} (2)$$
where $$$x$$$ refer to dMRI signals from different diffusion directions, $$$g$$$ refers to the diffusion direction, $$$\theta$$$ represents the angular difference and $$$a$$$ is a hyperparameter controlling signal smoothness within a shell.
To exploit shared information cross shells, we extend the single-shell DAGER to multi-shell by adding a squared-exponential function to the GP covariance function:
$$c(x,x′)=C_\theta (arccos|⟨g,g′⟩|;a)exp(-\frac{(logb-logb')^2}{2l^2} ) (3)$$
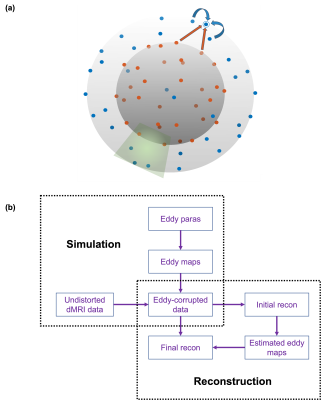
where $$$b$$$ is the b value, $$$l$$$ is a hyperparameter controlling signal smoothness between shells. With this formulation, sharable information between different shells can be incorporated into the reconstruction as shown in Fig.1 (a).
ems-DAGER incorporates GP estimated multi-shell dMRI signal as a prior and solves the following reconstruction problem:
$$u=\min_{u} (\frac{1}{2\sigma _k^2}\left \| Au-d \right \|^2_2+\frac{1}{2}(u-\mu )^H(\sum \otimes I_N)^{-1}(u-\mu ) ) (4)$$
where $$$u$$$ is the unknown image, $$$\sigma _k$$$ is the noise standard deviation, $$$A$$$ is the encoding matrix, $$$d$$$ is the acquired signal, $$$\mu$$$ is the mean value of GP prediction, $$$\sum$$$ represents the covariance matrix generated from $$$C$$$ and $$$ N$$$ is the number of voxels. The problem is solved using gradient descent method.
Eddy current-corrected reconstruction
Eddy current-induced distortions lead to mismatch between diffusion directions. At opposite sides of the sphere, the q-space points share the same diffusion contrasts yet eddy currents induce opposite distortions, which undermines the locally coherent assumption in DAGER. In this work, we propose a 2-step reconstruction to tackle this problem. In step 1, we use single-shell DAGER without using antipodal symmetric property to reconstruct the data shell-by-shell. This initial reconstruction is used to estimate eddy current induced B0 field inhomogeneity with FSL’s Eddy16. These eddy current terms are then incorporated into the encoding matrix $$$A$$$ that maps the undistorted image $$$u$$$ to distorted k-space data $$$d$$$. In step 2, we perform ems-DAGER reconstruction using antipodal symmetric property. The full pipeline for ems-DAGER is shown in Fig.1 (b).
Dataset
Simulations were constructed based on HCP17 dMRI data using a ball-and-stick model. A 100-direction dataset was generated with 50 b=1000s/mm2 and 50 b=2000s/mm2 images uniformly sampled in q-space, representing a widely used multi-shell dMRI protocol (e.g., UKBiobank18). A 64-direction dataset consisting of 32 b=1000s/mm2 and 32 b=2000s/mm2 images uniformly sampled in q-space was also generated to evaluate the performance of ems-DAGER with a small number of diffusion directions. Eddy-current-induced field inhomogeneity was measured from a phantom using the same diffusion directions and b values on a 3T Siemens scanner. A graph model based approach11 was applied to design a k-q undersampling where a local q-space neighbourhood across two shells has diverse k-space undersampling patterns. Under-sampled multi-channel datasets were simulated with sensitivity maps from an 8-channel head coil and R=4/6.
Results
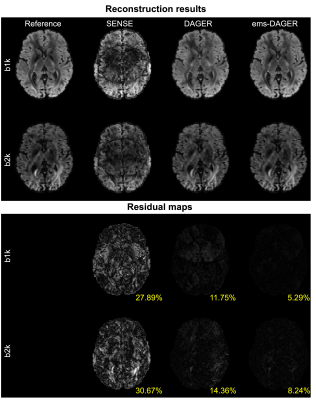
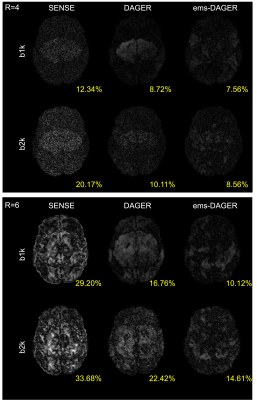
Fig.2 compares the proposed ems-DAGER with the single-shell DAGER for the 100-direction data, which both include eddy correction. The use of multi-shell information substantially improves the image quality, outperforming original DAGER method which only exploits information from a single-shell.The reconstruction results and corresponding residual maps for the 64-direction data are shown in Fig. 3 and Fig. 4, respectively. Single-shell DAGER breaks down with large aliasing due to the limited number of directions per shell. In comparison, ems-DAGER provides higher reconstruction accuracy. Notably, for R=6 with only 8 coils, ems-DAGER is still able to reconstruct images without major errors, indicating the efficacy of utilizing multi-shell information.
The improvement in image quality translates to the color-coded fractional anisotropy (cFA) (Fig. 5) maps. Due to the residual aliasing artifacts, the cFA maps obtained from SENSE show strong artifacts. While the single-shell DAGER method can improve the image quality, the result still shows higher noise levels and inconsistent color patterns from the reference. ems-DAGER produces cFA maps which best delineate brain structure.
Conclusion
We extended the DAGER method to jointly reconstruct multi-shell dMRI images with eddy-current correction. We demonstrated that the introduction of multi-shell information can improve the reconstruction performance regarding SNR and artifact suppression. Our future research will investigate the performance of ems-DAGER in vivo.Acknowledgements
W.W. is supported by the Royal Academy of Engineering (RF\201819\18\92). K.L.M. is supported by the Wellcome Trust (WT202788/Z/16/A). The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z).References
1. Bammer R. Basic principles of diffusion-weighted imaging. Eur J Radiol 2003;45(3):169-184.
2. Basser, P.J., Mattiello, J. and LeBihan, D., 1994. MR diffusion tensor spectroscopy and imaging. Biophysical journal, 66(1), pp.259-267.
3. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002;47:1202–1210.
4. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962.
5.Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 2012;67(5):1210-1224.
6. Menzel, M.I., Tan, E.T., Khare, K., Sperl, J.I., King, K.F., Tao, X., Hardy, C.J. and Marinelli, L., 2011. Accelerated diffusion spectrum imaging in the human brain using compressed sensing. Magnetic Resonance in Medicine, 66(5), pp.1226-1233.
7. Bilgic, B., Setsompop, K., Cohen‐Adad, J., Yendiki, A., Wald, L.L. and Adalsteinsson, E., 2012. Accelerated diffusion spectrum imaging with compressed sensing using adaptive dictionaries. Magnetic Resonance in Medicine, 68(6), pp.1747-1754.
8. Chao TC, Chiou JG, Maier SE, Madore B. Fast diffusion imaging with high angular resolution. Magn Reson Med 2017;77(2):696-706.
9. Mani M, Jacob M, Guidon A, Magnotta V, Zhong J. Acceleration of high angular and spatial resolution diffusion imaging using compressed sensing with multichannel spiral data. Magn Reson Med 2015;73(1):126-138.
10.Shi X, Ma X, Wu W, Huang F, Yuan C, Guo H. Parallel imaging and compressed sensing combined framework for accelerating high-resolution diffusion tensor imaging using inter-image correlation. Magn Reson Med 2015;73(5):1775-1785.
11.Wu W, Koopmans PJ, Andersson JLR, Miller KL. Diffusion Acceleration with Gaussian process Estimated Reconstruction (DAGER). Magn Reson Med 2019;82(1):107-125.
12. Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 2016;125:1063-1078.
13. Jensen, J.H., Helpern, J.A., Ramani, A., Lu, H. and Kaczynski, K., 2005. Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 53(6), pp.1432-1440.
14. Zhang, H., Schneider, T., Wheeler-Kingshott, C.A. and Alexander, D.C., 2012. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage, 61(4), pp.1000-1016.
15. Andersson JL, Sotiropoulos SN. Non-parametric representation and prediction of single- and multi-shell diffusion-weighted MRI data using Gaussian processes. Neuroimage 2015;122:166-176.
16. Sotiropoulos SN, Jbabdi S, Xu JQ, et al. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage 2013;80:125-143.
17.Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. Fsl. Neuroimage. 2012;62(2):782-790.
18. Miller KL, Alfaro-Almagro F, Bangerter NK, Thomas DL, Yacoub E, Xu J, Bartsch AJ, Jbabdi S, Sotiropoulos SN, Andersson JL, Griffanti L, Douaud G, Okell TW, Weale P, Dragonu I, Garratt S, Hudson S, Collins R, Jenkinson M, Matthews PM, Smith SM. Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nat Neurosci 2016;19(11):1523-1536.
Figures