3959

Self-Calibrated Subspace Reconstruction using Temporally Local Matrix Completion for Multidimensional MR Fingerprinting

Zhilang Qiu¹, Siyuan Hu¹, Walter Zhao¹, Ken Sakaie², Mark A. Griswold³, Derek K. Jones⁴, and Dan Ma¹
¹Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, ²Imaging Institute, Cleveland Clinic, Cleveland, OH, United States, ³Radiology, Case Western Reserve University, Cleveland, OH, United States, ⁴Cardiff University Brain Research Imaging Centre (CUBRIC), School of Psychology, Cardiff University, Cardiff, United Kingdom

Synopsis

Keywords: Image Reconstruction, Diffusion/other diffusion imaging techniques

We propose a new reconstruction method, named self-calibrated subspace reconstruction, for multidimensional MR fingerprinting (mdMRF), in order to correct the artifacts due to inter-shot (segment) magnitude and phase variations, without the need for extra navigator or calibration data. Different options for utilizing the low-rank property and the signal structure of mdMRF data are investigated and the optimal scheme is determined. Such that aliasing-free high-resolution image reconstruction and high-quality quantification, can be achieved.

Introduction

Previously, a multidimensional MR Fingerprinting framework (mdMRF) has been developed for joint relaxation and diffusion quantification [1]. Because a diffusion-prepared SSFP acquisition scheme [2-4] was applied, pulsation motion caused inter-shot magnitude and phase variations could happen at random locations. In this work, we propose a new reconstruction method for mdMRF, to address the artifacts caused by inter-shot and intra-shot magnitude and phase variations, without the need for pulsation gating, extra navigator [5], real time calibration data [6], or fully-sampled central k-space [7]. We further investigate different options for utilizing the low-rank property, and determine the optimal scheme which can fully utilize the signal structure in mdMRF, allowing aliasing-free high-resolution image reconstruction, and high-quality quantification.

Theory

The proposed method contains two procedures:

(1) Temporally Local Low-Rank Matrix Completion
First, we apply a low-rank matrix completion method [7, 8] on the under-sampled central k-space to obtain aliasing-free low-resolution images that served as calibration data. However, the temporally global low-rank property, which is commonly assumed for MRF data [7, 9], is weakened by inter-shot magnitude and phase variations.

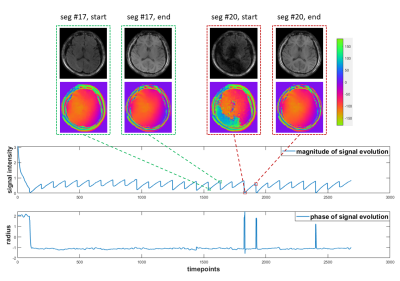
Figure 1 summarizes the inter- and intra-shot magnitude and phase variations during an mdMRF in vivo scan. Inter- and intra-shot (segment) magnitude and phase variations are highlighted.

Given the weak correlation between the inter-shot magnitude and phase variations induced by physiological motion, the temporally global low-rank property would be greatly weakened, making the low-rank matrix completion fail. Fortunately, the temporally local (segment-wise) low-rank property is still satisfied, because the phase variation in each diffusion preparation can be viewed as an additional “tissue property” within the segment. Therefore, we use a temporally local low-rank matrix completion in the first procedure.

(2) Temporally Global Subspace Reconstruction
Because the low-resolution and high-resolution mdMRF data share the same temporal subspace, temporally subspace reconstruction is proposed for high-resolution images from the under-sampled full k-space, where the subspace is estimated from the calibration data obtained in the first procedure. This is related to subspace reconstruction [10], which is essentially a linear reconstruction exploring a low-dimensional signal structure [11] given the subspace known, where the performance would be greatly benefited from more data sharing.

Validation

Figure 2A shows the flowcharts of the proposed reconstruction and its validation. The reconstruction contains two procedures. The first is to obtain a fully sampled low-resolution calibration data from the under-sampled central k-space, using temporally local (segment-wise) matrix completion. The second is to obtain aliasing-free high-resolution images from the under-sampled whole k-space, using subspace reconstruction, where the temporally global subspace is estimated from the calibration data obtained in the first procedure. Figure 2B shows the validation steps that evaluate different reconstruction options. Specifically, for the first step that aims to generate calibration images to capture corrupted images, we compare image quality of using central or full k-space data, and using global or local temporally low-rank matrix completion. For the second step that aims to generate high resolution MRF images, we compare the image quality of using temporally local or global or joint low rank subspace reconstruction. The corrupted segments (or images) were detected by a customized outlier detection algorithm, and excluded in the mapping step using pattern matching [9] to generate T1, T2 and ADC maps simultaneously.

Results

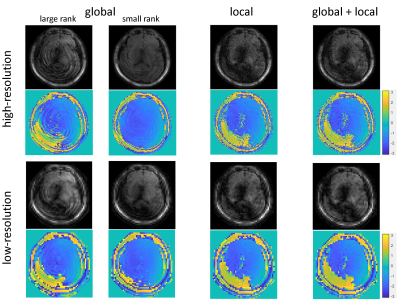
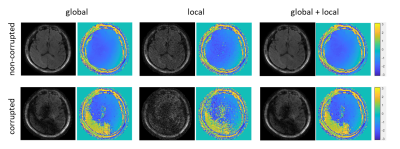
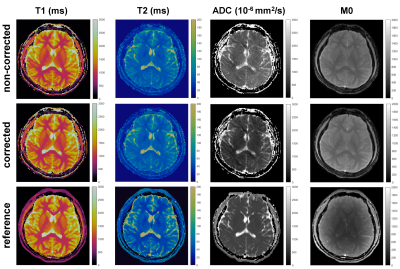
Figure 3 compares three options for the first procedure. Temporally global low-rank matrix completion fails to obtain an accurate calibration data. Specifically, when a large rank (=40) is chosen as a stopping criterion, the aliasing artifacts are still severe. In contrast, when a small rank (=8) is chosen, the signal components corresponding to small singular values (e.g., the phase information) are lost. The temporally local low-rank matrix completion significantly reduces the aliasing artifact, and capture the signal components corresponding to small singular values (e.g., the phase variations). Joint global and local low-rank matrix completion has negligible improvement compared to the local matrix completion. Therefore, temporally local matrix completion is chosen to obtain a low-resolution calibration data. Figure 4 shows that reconstructed images using temporally local subspace possess lower SNR than those using temporally global subspace. Joint global and local subspace reconstruction have slight improvement compared to those from global subspace reconstruction, and the improvement is more significant in the corrupted images. This indicates an effective joint utilization of global and local low-rank properties. In practice, the temporally global subspace reconstruction is chosen for this procedure, because the difference is slight and the subsequent dictionary matching [9] can further correct for incoherent artifacts. Figure 5 shows the quantitative maps obtained by mdMRF without pulsation gating. The ADC map in the non-corrected case has severe shading artifacts, which appear as uneven and overestimated ADC values. The artifacts can be addressed after correction.

Discussion and Conclusion

In this work, a self-calibrated subspace reconstruction using temporally local low-rank matrix completion, which takes advantage of the temporally local low-rank property of mdMRF data, to address weakened global low-rank assumption caused by inter-shot (segment) magnitude modifications and phase variations. No extra navigator, realtime calibration data, or fully-sampled central k-space is required. Aliasing-free high-resolution images can be reconstructed and corrected to generate artifact-free T1, T2, and ADC maps.

Acknowledgements

This work was supported by Siemens Healthineers and NIH grant R01 NS1094391.

References

1. Afzali M, et al. MR Fingerprinting with b‐Tensor Encoding for Simultaneous Quantification of Relaxation and Diffusion in a Single Scan. Magn Reson Med. 2022;88:2043-2057.

2. Jeong EK, et al. High-resolution diffusionweighted 3D MRI, using diffusion-weighted driven-equilibrium (DW-DE) and multishot segmented 3D-SSFP without navigator echoes. Magn Reson Med. 2003;50:821-829.

3. Nguyen C, et al. In vivo three-dimensional high resolution cardiac diffusion-weighted MRI: a motion compensated diffusion-prepared balanced steady-state free precession approach. Magn Reson Med. 2014;72:1257-1267.

4. Lu L, et al. Diffusion‐prepared fast imaging with steady‐state free precession (DP‐FISP): a rapid diffusion MRI technique at 7 T. Magn Reson Med. 2012;68:868-73.

5. Cao X, et al. 3D Diffusion-prepared MRF (3DM) with cardiac gating for rapid high resolution whole-brain T1, T2, proton density and diffusivity mapping. Proc Intl Soc Mag Reson Med. 2022.

6. Ma S, et al. Three‐dimensional simultaneous brain T1, T2, and ADC mapping with MR Multitasking. Magn Reson Med. 2020;84:72-88.

7. Doneva M, et al. Matrix completion-based reconstruction for undersampled magnetic resonance fingerprinting data. Magn Reson Imaging. 2017;41:41-52.

8. Candes EJ, Recht B. Exact matrix completion via convex optimization. Found Comput Math. 2009;9:717–72.

9. Ma D, et al. Magnetic resonance fingerprinting. Nature. 2013;495:187-192.

10. Liang ZP. Spatiotemporal imagingwith partially separable functions. In2007 4th IEEE international symposium on biomedical imaging: from nano to macro 2007 Apr 12 (pp. 988-991). IEEE.

11. Tamir JI, et al. Computational MRI with physics-based constraints: Application to multicontrast and quantitative imaging. IEEE signal processing magazine. 2020 Jan 17;37(1):94-104.

Figures

Figure 1. Images corresponding to four representative time points (the first and the last images of the non-corrupted and corrupted segments, respectively). The solid and hollow arrows point out the magnitude variations (signal dropouts) and phase variations, respectively.

Figure 2. The flowcharts of the proposed reconstruction (A) and its validation (B).

Figure 3. Performance evaluation of the temporally local low-rank matrix completion in the first procedure of the proposed reconstruction. It is compared to the other two alternatives (temporally global, and joint global and local matrix completion). Both high-resolution and low-resolution cases are evaluated to see the consistency.

Figure 4. Performance evaluation of the temporally global subspace reconstruction in the second procedure. It is compared to the other two alternatives (temporally local, and joint global and local subspace reconstruction). Images corresponding to two representative timepoints (one is not corrupted and the other corrupted) are shown.

Figure 5. In vivo T1, T2, ADC, and proton density (M0) maps obtained by mdMRF without pulsation gating using the proposed self-calibrated subspace reconstruction. The non-corrected case and corrected case, as well as the reference, are compared.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

3959

DOI: https://doi.org/10.58530/2023/3959