3941
Predicting Uncertainty of Metabolite Quantification in Magnetic Resonance Spectroscopy with Applications for Adaptive Ensembling
Julian P. Merkofer1, Sina Amirrajab1, Johan S. van den Brink2, Mitko Veta1, Jacobus F. A. Jansen1,3, Marcel Breeuwer1,2, and Ruud J. G. van Sloun1,4
1Eindhoven University of Technology, Eindhoven, Netherlands, 2Philips Healthcare, Best, Netherlands, 3Maastricht University Medical Center, Maastricht, Netherlands, 4Philips Research, Eindhoven, Netherlands
1Eindhoven University of Technology, Eindhoven, Netherlands, 2Philips Healthcare, Best, Netherlands, 3Maastricht University Medical Center, Maastricht, Netherlands, 4Philips Research, Eindhoven, Netherlands
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Spectroscopy, Deep Learning, Uncertainty Prediction, Adaptive Ensemble
Current deep learning methods for metabolite quantification in magnetic resonance spectroscopy do not offer reliable measures for uncertainty. Having a widely applicable measure can aid with the identification of fitting errors and enable uncertainty-based adaptive ensembling of model-based quantification and neural network predictions. In this abstract, we propose a training strategy based on a log-likelihood cost that allows joint optimization of concentration and uncertainty estimation for each individual metabolite. We show that the predicted uncertainties correlate well with the actual estimation errors and that uncertainty-based adaptive ensembling outperforms the individual estimators as well as standard ensembling.Introduction
Deep learning (DL) methods have increasingly been introduced for metabolite quantification in magnetic resonance spectroscopy (MRS)1-3. However, the explored implementations do not offer reliable measures for the uncertainty of their predictions, hindering their clinical applicability. A proposed method based on the construction of a database during training consisting of signal-to-noise ratio (SNR), linewidth, and signal-to-background has already been introduced4, yet the method lacks scalability and transferability to various DL architectures. Furthermore, a recent analysis of the reliability of DL methods for quantification in MRS has highlighted and addressed certain model and data biases5, emphasizing the need for widely applicable uncertainty estimation for DL in MRS. Reporting uncertainty does not only allow identification of potential fitting errors, but also enables uncertainty-based adaptive ensembling of classic model-based (MB) fitting and DL predictions. Ensembling techniques have been shown to improve performance, generalizability, and robustness over individual estimation algorithms6.In this abstract, we propose a training strategy based on a log-likelihood cost function that allows joint optimization of concentration and uncertainty estimation for each individual metabolite through an auxiliary neural network (NN) output. Furthermore, we demonstrate its feasibility by utilizing the uncertainty predictions as mixing coefficients for adaptive ensembling. On artificial data, we show that the predicted uncertainty correlates well with the actual estimation error, and we benchmark the adaptive ensembling against the individual estimators as well as against standard ensembling (using constant and uniform mixing coefficients).
Methods
The MRS signal model for the simulation of the MRS spectra used to train the proposed DL method takes the following form of a standard Voigt line-shaped model: $$X(f) = e^{i (\phi_0 + f \phi_1)} \sum^{M}_{m=1} a_{m} \ FFT\left\{s_{m}(t) \ e^{- (i \epsilon + \gamma + \varsigma^2 t) t} \right\} + B(f), \qquad {(Eq. \ 1)}$$ where $$$\epsilon$$$, $$$\gamma$$$, and $$$\varsigma$$$ account for Lorentzian and Gaussian broadening. The metabolite basis set $$$\{s_{m}\}_{m=1}^M$$$ is taken from the ISMRM 2016 fitting challenge data7 (consisting of 21 metabolite spectra and a macromolecule spectrum). The baseline $$$B(f) $$$ is represented by a second-order polynomial, $$$\phi_0$$$ and $$$\phi_1$$$ are the zero and first order phase corrections, and the $$$a_{m}$$$ are the concentrations of the $$$M$$$ metabolites of interest. The simulated dataset is obtained (using a Python script) by randomly drawing the model parameters from uniform distributions with ranges estimated from the challenge dataset along with adding Gaussian noise to the spectra (SNR ranging from 3-90).The NN architecture is visualized in Figure 1 and consists of a multi-layer perceptron (MLP) taking the stacked real and imaginary part of the spectra (in the range of 0.2 to 4.2 ppm) as input. The network has two separate outputs for the concertation estimates $$$\boldsymbol{a}_{(pred)} = (a_1, …, a_M)$$$ as well as the corresponding uncertainties $$$\boldsymbol{\sigma}_{(pred)} = (\sigma _1, …, \sigma _M)$$$. The MLP is trained utilizing the following cost function, derived from the negative log-likelihood8,$$\mathcal{L} \left( \boldsymbol{a}_{(true)}, \boldsymbol{a}_{(pred)}, \boldsymbol{\sigma}_{(pred)} \right) = \frac{1}{2} \left( \ln{(\boldsymbol{\sigma}^2_{(pred)})} + \frac{\left( \boldsymbol{a}_{(true)} - \boldsymbol{a}_{(pred)}\right)^2}{\boldsymbol{\sigma}^2_{(pred)}} \right), \qquad {(Eq. \ 2)}$$ thereby, leveraging the quantification error and the predicted uncertainty. By adaptively combining the NN quantifications with the estimated concentrations of a linear combination modelling (LCM) algorithm $$$\boldsymbol{a}_{(lcm)}$$$ based on the predicted uncertainty we obtain an improved estimate$$\boldsymbol{a}_{(ens)} = (1 - \boldsymbol{w}) \ \boldsymbol{a}_{(lcm)} + \boldsymbol{w} \ \boldsymbol{a}_{(pred)}, \quad \boldsymbol{w} = 1 - \min{\left( \frac{\boldsymbol{\sigma}_{(pred)}}{\sigma_{max}}, 1 \right)}. \qquad {(Eq. \ 3 \ \& \ 4)}$$Thereby, the uncertainty sensitivity $$$\sigma_{max}$$$ allows to control the prediction certainty of the NN required to influence the ensemble concentration estimates.
Results & Discussion
Figure 2 depicts the correlation of the proposed uncertainty measure and the actual concentration estimation error for a testset of one thousand spectra of the artificially generated data. These results illustrate the effectiveness of the uncertainty prediction and highlight that for high estimation error a consistently high uncertainty is reported.For a comparison with commonly used uncertainty estimation in MRS, Figure 3 reports the correlation plots on the same test data for the Cramér-Rao lower bound (CRLB), CRLB percentage values (CRLB%), and the residual sum of squares (RSS) of the spectral fit of a LCM method. Note that the CRLB (and the CRLB%) merely report a lower bound on the variance of the estimation.
Figure 4 shows the mean absolute error (MAE) obtained by quantifying the metabolites of the 28 spectra of the ISMRM 2016 fitting challenge data7.
- Pure NN corresponds to the metabolite concentration output of the trained MLP.
- LCM Method refers to a standard least squares fitting method based on a pseudo-Newton approach.
- Standard ensembling consists of uniformly averaging the concentration estimates of the previously introduced methods.
- Adaptive ensembling depicts the concentrations $$$\boldsymbol{a}_{(ens)}$$$ for various uncertainty sensitivities $$$\sigma_{max}$$$.
Conclusions
We presented a training strategy based on a negative log-likelihood loss that enables uncertainty estimation for supervised DL quantification methods through an additional NN output. Furthermore, the proposed uncertainty measure shows good correlation with the actual estimation error and uncertainty-based ensembling outperforms both individual estimators as well as standard ensembling.Acknowledgements
This work was (partially) funded by Spectralligence (EUREKA IA Call, ITEA4 project 20209).References
- Dhritiman Das, Eduardo Coello, Rolf F. Schulte and Bjoern H. Menze. “Quantification of Metabolites in Magnetic Resonance Spectroscopic Imaging Using Machine Learning.” MICCAI (2017).
- Nima Hatami, Michaël Sdika, and Hélène Ratiney. “Magnetic Resonance Spectroscopy Quantification using Deep Learning.” MICCAI (2018).
- Saumya S. Gurbani, Sulaiman Sheriff, Andrew A. Maudsley, Hyunsuk Shim and Lee A. D. Cooper. “Incorporation of a spectral model in a convolutional neural network for accelerated spectral fitting.” Magnetic Resonance in Medicine 81 (2019): 3346-3357.
- Hyeong Hun Lee and Hyeonjin Kim. “Deep learning‐based target metabolite isolation and big data‐driven measurement uncertainty estimation in proton magnetic resonance spectroscopy of the brain.”Magnetic Resonance in Medicine 84 (2020): 1689-1706.
- Rudy Rizzo, Martyna Dziadosz, Sreenath P. Kyathanahally, Mauricio Reyes, and Roland Kreis. “Reliability of Quantification Estimates in MR Spectroscopy: CNNs vs Traditional Model Fitting.” MICCAI (2022).
- R. Maclin and David W. Opitz. “Popular Ensemble Methods: An Empirical Study.” J. Artif. Intell. Res. 11 (1999): 169-198.
- Malgorzata Marjanska, Dinesh K Deelchand, and Roland Kreis, “MRS fitting challenge datasetup by ISMRM MRS study group,” Type: dataset (2021).
- David A. Nix and Andreas S. Weigend. “Estimating the mean and variance of the target probability distribution.” Proceedings of 1994 IEEE International Conference on Neural Networks (ICNN'94) 1 (1994): 55-60 vol.1.
Figures
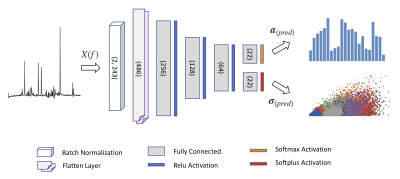
Figure 1: Visualizes the multi-layer perceptron (MLP) architecture for concurrent metabolite quantification and uncertainty estimation.
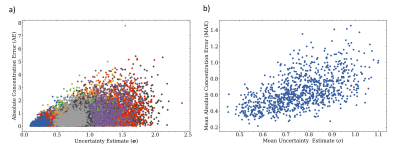
Figure 2: Correlation of the metabolite concentration error and the proposed uncertainty measure: a) depicted for individual metabolites (colors) and b) showing the mean error and uncertainty.

Figure 3: Depicts the correlation plots for: a) the Cramér-Rao lower bound (CRLB), b) the CRLB percentage values (CRLB%), and c) the residual sum of squares (RSS).
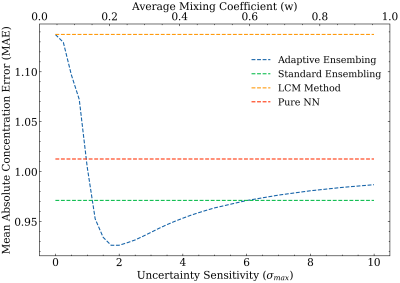
Figure 4: Shows the performance optimization of the proposed adaptive ensembling by combining the concentration estimates of a classic linear combination modelling (LCM) approach and a pure neural network (NN).
DOI: https://doi.org/10.58530/2023/3941