3934
Rejecting or retaining motion corrupted transients in diffusion-weighted MRS: high b-values and multiple directions
Clémence Ligneul1, Jesper Andersson1, Saad Jbabdi1, Jason Lerch1,2,3, and William T Clarke1
1Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 2Mouse Imaging Centre, The Hospital for Sick Children, Toronto, ON, Canada, 3Department of Medical Biophysics, University of Toronto, Toronto, ON, Canada
1Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 2Mouse Imaging Centre, The Hospital for Sick Children, Toronto, ON, Canada, 3Department of Medical Biophysics, University of Toronto, Toronto, ON, Canada
Synopsis
Keywords: Data Processing, Spectroscopy, Diffusion-weighted spectroscopy
Robust processing is crucial for a reliable microstructural interpretation of advanced diffusion-weighted magnetic resonance spectroscopy (DW-MRS) methods. The spectral signal intensity depends on the direction when using strong diffusion-gradients and multiple directions, even more if the voxel content is very anisotropic (e.g. contains a white matter tract). In this study we propose a model-based way of identifying motion corrupted averages that accounts for the voxel anisotropy.Introduction
Diffusion-weighted magnetic resonance spectroscopy (DW-MRS) provides non-invasive access to morphological properties and cytoarchitecture of neuronal and glial populations by measuring diffusion properties of intracellular and partly cell-specific endogenous metabolites[1].The diffusion gradients in DW-MRS make it particularly sensitive to motion. Even subtle (and often involuntary) movements of the subject can corrupt the DW-MRS signal. The extraction of meaningful microstructural parameters from DW-MRS data modeling depends on meticulous signal processing[2]. Inspired by dMRI methods[3], in this work we propose a robust, model-based way of identifying motion corrupted averages.
The current recommended method in conventional MRS for signal rejection[4] is described in[5]. This current method computes the RMS deviation of each transient (mi) from the mean of all transients and rejects transients which differ more than a predefined number of standard deviations from the mean. Normally, this method is applied in DW-MRS at each b-value independently, which means the greater motion sensitivity of high b-value-data biases the estimation of deviation variance, resulting in inappropriate retention of corrupted transients. Here, we propose a rejection/retention algorithm which simultaneously uses information from all b-values (and directions) combined with standard diffusion modelling (diffusion tensor + kurtosis, Fig.1).
Methods
Principle (Fig.1)For each spectral transient i, the mean absolute upfield signal (Mup,i) and the mean downfield signal (Mdown,i) are calculated (Fig2.a) in order to: minimise water signal contribution whose diffusion properties are very different from metabolites, and provide a (mostly) signal free reference region respectively:
$$M_{up,i}=\frac{1}{N}\sum_{\delta>1.9ppm}^{\delta<4.5ppm}\left|m_{i,\delta}\right|,\ {\ \ \ \ \ \ \ \ M}_{down,i}=\frac{1}{N}\sum_{\delta>6.8ppm}^{\delta<9.5ppm}\left|m_{i,\delta}\right|$$
The diffusion tensor is then calculated from the mean upfield signal (Mup,i) of all the transients, using an in house implementation relying on a linear regression of log(Mup,i). To more accurately model high b-values (b ⪆ 6 ms/µm2) an additional kurtosis term was added and the mean signal for each b-value (ignoring direction dependance) was recentred based on the median of transients with that b-value (final estimated signal shown as black line on Fig.2b).
For each Mup,i two predicted signals were generated: the isotropic (direction independent, b-value dependent) prediction $$${\hat{M}}_{up,i}^{iso}$$$, and the anisotropic (direction and b-value dependent) prediction $$${\hat{M}}_{up,i}^{DTI}$$$.
The noise characteristics of each transient are not dependent on diffusion encoding (direction or b-value) as only the metabolites signal is attenuated. The median absolute deviation (MAD) derived at b0, which is less sensitive to motion artefacts, is then used for higher b-values.
Rejection was then performed for each independent transient i according to
$$M_{up,i}<\ {\hat{M}}_{up,i}^{{DTI/iso}}-\ \alpha\ast\ MAD\left(b_0\right),\ \ \alpha=3$$
Rejection using $$${\hat{M}}_{up,i}^{DTI}$$$ is labelled ‘proposed approach’, rejection using $$${\hat{M}}_{up,i}^{iso}$$$ is labelled ‘isotropic approach’. Note, only the “negative” outliers are discarded (i.e. corresponding to a signal drop). “Positive” outliers are possible , but unlikely to occur compared to motion-driven signal loss.
Data
The approach is demonstrated on two datasets acquired on a Bruker Biospec 7T (Gmax=660mT/m, mouse quadrature cryocoil). One dataset was acquired in the mouse hippocampus and has low motion corruption (“good”). The second dataset was acquired in the cerebellum of a P20 rat and has high levels of motion corruption (“challenging”). Both contain six b-values [0.03 3.03 6 10 20 30]ms/µm2, and 16 directions for each b-value. The number of repetitions for each direction/b-value pair was increased with b-value (4, 4, 6, 6, 8, 8). Both voxels contain white matter (corpus callosum or vermis).
Results
When data are not corrupted by motion (Fig.2b) and the data is not highly anisotropic (FA=0.08), all approaches (current, isotropic and proposed) perform similarly. However, when data contains motion artefacts (Fig.2b, right), the “current approach” keeps transients clearly corrupted by motion. This is exemplified in Fig.2a where the purple spectrum shows a substantial signal drop in both metabolite and macromolecular signal at 0.9ppm (which should show very limited diffusion attenuation[6]), but is retained in the current approach. The proposed approach discards this transient.Discussion & Conclusions
Here we have proposed a first implementation of a new method for rejecting DW-MRS transients corrupted by motion. In a small sample of data this has been shown to be effective in data with anisotropic diffusion measured using multiple directions. The effect on the powder average signal decay is illustrated in Fig3. The “good” dataset barely exhibits any difference between approaches, while the “challenging” dataset demonstrates higher improvement from both the isotropic and proposed approaches over the current.Future work will:
1) evaluate the benefit of the proposed approach in more and highly anisotropic data (e.g. human white matter),
2) Implement an iterative approach to mitigate the effect of badly corrupted transients on the estimation of the diffusion tensor,
3) Utilise the variance across all b-values to help estimate the MAD.
Acknowledgements
WTC acknowledges grant funding from the Wellcome Trust [225924/Z/22/Z] and [224430/Z/21/Z]. The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z and 203139/A/16/Z).References
[1] Ronen et Valette, eMagRes, 2015
[2] Najac et al., ISMRM proceedings 2021, program number #2616
[3] Andersson et al., NeuroImage, 2016
[4] Near et al., NMR in Biomed, 2020
[5] Simpson et al., MRM, 2017
[6] Ligneul et al., NMR Biomed, 2017
Figures

Figure 1: Principle of the proposed approach. The diffusion tensor is estimated from the mean upfield signal of the spectral transients to predict the acceptable signal range for transients with variable b-values and diffusion directions.
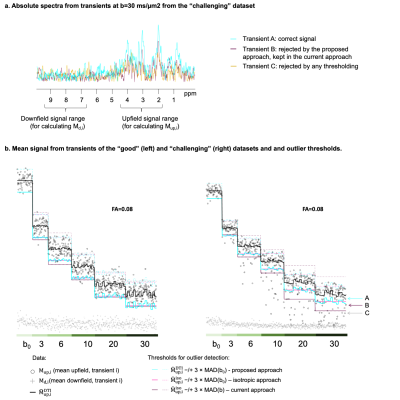
Figure 2: (a) Absolute spectra from transients A, B and C coming from the “challenging” dataset. A line broadening of 20Hz is applied for visualisation purposes. (b) Mean upfield signal of all transients for both datasets.
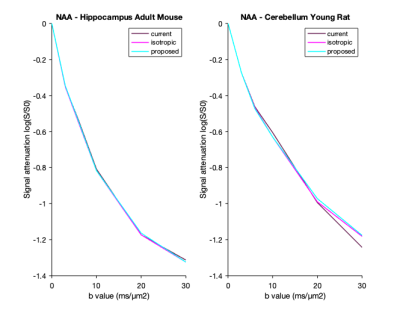
Figure 3: Effect of the current, isotropic and proposed approaches on fitted N-acetypaspartate signal attenuation in the “good” (left) and the “challenging“ (right) datasets.
DOI: https://doi.org/10.58530/2023/3934