3913
Boosting Central Head SNR at 10.5T: 32-channel Hybrid RF Coil Comprised of 25 Rx-only Loops and 7 TxRx NODES Dipoles
Alireza Sadeghi-Tarakameh1, Matt Waks1, Andrea Grant1, Jeromy Thotland1, Russell L Lagore1, Lance DelaBarre1, Edward Auerbach1, Pierre‐Francois Van de Moortele1, Gregor Adriany1, Kamil Ugurbil1, and Yigitcan Eryaman1
1Center for Magnetic Resonance Research (CMRR), University of Minnesota, Minneapolis, MN, United States
1Center for Magnetic Resonance Research (CMRR), University of Minnesota, Minneapolis, MN, United States
Synopsis
Keywords: RF Arrays & Systems, High-Field MRI
Higher signal-to-noise ratio (SNR) is the primary maxim for increasing the magnetic field strength of MRI scanners. However, RF coils comprised of loops do not capture the highest achievable SNR that is theoretically available at ultrahigh field (defined as ≥7T) MRI. In this study, we investigate the hypothesis of increasing central head SNR at 10.5T by combining loop and dipole receiver elements. For this purpose, we manufactured a 32-channel hybrid RF coil comprised of 25 receive-only loops and 7 transceiver NODES dipoles. This 32ch hybrid coil achieved ~80% higher central SNR compared to a 32ch loop array.Introduction
The primary justification for the higher magnetic field strengths is the inherently higher signal-to-noise ratio (SNR)1-5 which can be exploited for higher spatiotemporal resolution and/or contrast. Despite notable achievements using ultrahigh field (UHF, defined as ≥7T) scanners, the highest theoretically available SNR is, in practice, not fully captured, especially for applications involving the central regions of the human brain.The analytic expression for ultimate intrinsic SNR (UISNR)6,7 shows that the UISNR at the center of a uniform sphere phantom increases with exponent 2.13 of the field strength (B0). Given the UISNR theory6,7 and practical observations8, more than a 2-fold central SNR gain is expected, increasing the B0 from 7T to 10.5T. However, a 32-channel loop Rx array at 10.5T9 achieved only a 1.5-fold higher SNR at the center of a uniform head-shaped phantom compared to the 32-channel NOVA coil (Nova Medical Inc.). On the other hand, Lattanzi et al.10 theoretically calculated the ideal current patterns that lead to the UISNR at different field strengths (from 0.2T to 11T) at the center of a uniform cylindrical phantom. Their findings show that at 0.2T, the divergence-free pattern (electric-loop) dominates, whereas, at higher field strengths (particularly >7T), the curl-free pattern (electric-dipole) dominates. Wiggins et al.11 proposed loop-dipole (LD) combinations. LD transceiver arrays showed promising results for body12 and head13,14 at UHF. Lagore et al.15 and Avdievich et al.16 recently combined 8 transceiver dipoles with 24 loop receivers for 32-channel head coils at 10.5T and 7T, respectively. Avdievich et al.16 reported up to 25% higher SNR at the center of a human head (in vivo) compared to the 32-channel NOVA coil.
In this study, we numerically and experimentally investigate the hypothesis of central SNR improvement using a loop-dipole array for 10.5T head imaging. For this purpose, 7 receive (Rx)-only loops from a 32-channel loop array9 were replaced by 7 transceive (TxRx) NODES dipoles17 (physically short dipoles). The Rx and Tx performances of this 32ch hybrid array were compared to those of 32ch loop Rx9 and 8ch bumped dipole Tx arrays18, respectively, inside a uniform phantom at 10.5T.
Methods
We previously optimized a NODES configuration for a deep-body target application (i.e., 50mm to 100mm depth) at 10.5T17. For this, two separate optimization problems were solved using an exhaustive search over the results obtained from fast EM simulations inside a uniform phantom17. The objectives of these optimization problems were to maximize the SAR efficiency ($$$\xi(r)=\frac{B_1^+(r)}{\sqrt{pSAR_{10}}}$$$) and intrinsic SNR ($$$\psi(r)\sim\frac{B_1^-(r)}{\sqrt{P_{in}}}$$$) at the depth-of-interest, where $$$pSAR_{10}$$$ is the peak 10g-averaged local specific absorption rate (SAR) and $$$P_{in}$$$ is the input power. The optimized NODES configurations for SAR and SNR are shown in Fig. 1A and 1B, respectively. For this study, the NODES element shown in Fig. 1C is constructed with some practical considerations. Since the constructed NODES element is not identical to either SAR-optimum or SNR-optimum configuration, its Tx and Rx performances deviate from the optimal results by 12% and 23%, respectively (see Fig. 1D).Seven of the NODES dipoles shown in Fig. 1C were used to replace 7 loops of a 32ch Rx-only loop array (a modified version of the previously proposed 32ch array9), and eventually, construct a 32ch hybrid coil comprised of 25 Rx-only loops and 7 TxRx NODES dipoles. EM simulation models of the 32ch Rx-only and hybrid arrays are shown in Fig. 2A,B. Numerically and experimentally obtained 3D intrinsic SNR (ISNR) maps were used to compare the Rx performances of the two arrays inside a uniform phantom (εr = 47, σ = 0.65S/m). The Tx performance of the 7ch TxRx NODES array was compared to that of the 8ch TxRx bumped dipole array18 (Fig. 2C,E). Numerically obtained Tx efficiency ($$$\eta(r)=\frac{B_1^+(r)}{\sqrt{P_{in}}}$$$) and SAR efficiency ($$$\xi(r)=\frac{B_1^+(r)}{\sqrt{pSAR_{10}}}$$$) maps were used for this comparison.
Results
Fig. 3 shows the Tx and SAR efficiency maps corresponding to the circularly-polarized (CP) mode of the 8 bumped dipole and 7 NODES dipole arrays inside a uniform phantom. Despite the shorter length of the NODES dipole compared to bumped dipoles, Fig. 3 shows that similar Tx performance can be achieved with a similar number of elements.Fig. 4 and Fig. 5, respectively, show the numerically and experimentally acquired ISNR maps using the loop-NODES and loop-only 32ch arrays. The 32ch hybrid loop-NODES array achieved higher ISNR at the center compared to the 32ch Rx-only loop array by ~60% in simulation and ~80% in the experiment.
Discussions and Conclusion
In this study, we investigated the hypothesis that combining loop and dipole elements can increase the SNR at the center of human head at UHF MRI. For this purpose, we used our previously proposed NODES dipole17 in the transceiver mode. The physically short length of NODES dipoles enables the option of stacking Tx elements in the z-direction, which potentially can be used to lower the excitation inhomogeneity. We eventually validated the hypothesis at 10.5T by combining 7 TxRx NODES dipoles with 25 Rx-only loops and comparing its SNR performance to a 32ch Rx loop array. The loop-NODES array achieved 80% higher SNR at the center.Acknowledgements
This work was supported by the following grants: NIBIB P41 EB027061, NINDS R01NS115180 and NIH U01 EB025144.References
- Vaughan JT, Garwood M, Collins CM, Liu W, DelaBarre L, Adriany G, Andersen P, Merkle H, Goebel R, Smith MB. 7T vs. 4T: RF power, homogeneity, and signal‐to‐noise comparison in head images. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2001;46(1):24-30.
- Pohmann R, Speck O, Scheffler K. Signal‐to‐noise ratio and MR tissue parameters in human brain imaging at 3, 7, and 9.4 tesla using current receive coil arrays. Magnetic resonance in medicine. 2016;75(2):801-9.
- Ocali O, Atalar E. Ultimate intrinsic signal‐to‐noise ratio in MRI. Magnetic resonance in medicine. 1998;39(3):462-73.
- Wiesinger F, Boesiger P, Pruessmann KP. Electrodynamics and ultimate SNR in parallel MR imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2004;52(2):376-90.
- Guérin B, Villena JF, Polimeridis AG, Adalsteinsson E, Daniel L, White JK, Wald LL. The ultimate signal‐to‐noise ratio in realistic body models. Magnetic resonance in medicine. 2017;78(5):1969-80.
- Lee HH, Sodickson DK, Lattanzi R. An analytic expression for the ultimate intrinsic SNR in a uniform sphere. Magnetic resonance in medicine. 2018;80(5):2256-66.
- Hoult DI. Sensitivity and power deposition in a high‐field imaging experiment. Journal of Magnetic Resonance Imaging. 2000;12(1):46-67
- Le Ster C, Grant A, Van de Moortele PF, Monreal‐Madrigal A, Adriany G, Vignaud A, Mauconduit F, Rabrait‐Lerman C, Poser BA, Uğurbil K. Magnetic field strength dependent SNR gain at the center of a spherical phantom and up to 11. 7T. Magnetic resonance in medicine. 2022;88(5):2131-8.
- Tavaf N, Lagore RL, Jungst S, Gunamony S, Radder J, Grant A, Moeller S, Auerbach E, Ugurbil K, Adriany G. A self‐decoupled 32‐channel receive array for human‐brain MRI at 10.5 T. Magnetic resonance in medicine. 2021;86(3):1759-72.
- Lattanzi R, Sodickson DK. Ideal current patterns yielding optimal signal‐to‐noise ratio and specific absorption rate in magnetic resonance imaging: computational methods and physical insights. Magnetic resonance in medicine. 2012;68(1):286-304.
- Wiggins GC, Zhang B, Cloos M, Lattanzi R, Chen G, Lakshmanan K, Haemer G, Sodickson DK. Mixing loops and electric dipole antennas for increased sensitivity at 7 Tesla. InProceedings of the 21st Annual Meeting of ISMRM 2013 Apr 7 (p. 2737).
- Ertürk MA, Raaijmakers AJ, Adriany G, Uğurbil K, Metzger GJ. A 16‐channel combined loop‐dipole transceiver array for 7 T esla body MRI. Magnetic resonance in medicine. 2017 Feb;77(2):884-94.
- Woo MK, DelaBarre L, Lee BY, Waks M, Lagore RL, Radder JW, Eryaman Y, Ugurbil K, Adriany G. Evaluation of a 16-channel transceiver loop+ dipole antenna array for human head imaging at 10.5 tesla. IEEE Access. 2020 Nov 6;8:203555-63.
- Woo MK, Lagore RL, DelaBarre L, Lee BY, Eryaman Y, Radder J, Erturk A, Metzger G, van de Moortele PF, Ugurbil K, Adriany G. A geometrically adjustable loop-dipole (LD) head array for 10.5 T. InProceedings of the 25th Annual Meeting of ISMRM, Honolulu, HI 2017 Apr 22 (p. 1051).
- Lagore RL, Moeller S, Zimmermann J, DelaBarre L, Radder J, Grant A, Ugurbil K, Yacoub E, Harel N, Adriany G. An 8‐dipole transceive and 24‐loop receive array for non‐human primate head imaging at 10.5 T. NMR in Biomedicine. 2021 Apr;34(4):e4472.
- Avdievich NI, Nikulin AV, Ruhm L, Magill AW, Glang F, Henning A, Scheffler K. A 32‐element loop/dipole hybrid array for human head imaging at 7 T. Magnetic resonance in medicine. 2022;88(4):1912-26.
- Sadeghi‐Tarakameh A, Jungst S, Lanagan M, DelaBarre L, Wu X, Adriany G, Metzger GJ, Van de Moortele PF, Ugurbil K, Atalar E. A nine‐channel transmit/receive array for spine imaging at 10.5 T: Introduction to a nonuniform dielectric substrate antenna. Magnetic resonance in medicine. 2022;87(4):2074-88.
- Sadeghi‐Tarakameh A, DelaBarre L, Lagore RL, Torrado‐Carvajal A, Wu X, Grant A, Adriany G, Metzger GJ, Van de Moortele PF, Ugurbil K. In vivo human head MRI at 10.5 T: A radiofrequency safety study and preliminary imaging results. Magnetic resonance in medicine. 2020;84(1):484-96.
Figures
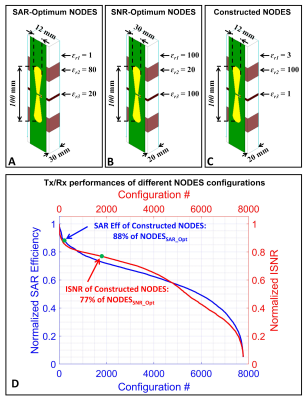
Figure 1. Tx and Rx performances of NODES
dipoles at 10.5T (averaged over depth of 50 to 100mm inside a uniform phantom).
The structures of (A) SAR-optimum, (B) SNR-optimum, and (C) Constructed NODES
dipoles. (D) Descending-sorted SAR efficiency and ISNR of ~8000 different NODES
configurations (normalized to the max value). Performance of the constructed
NODES is indicated by green points on each graph.
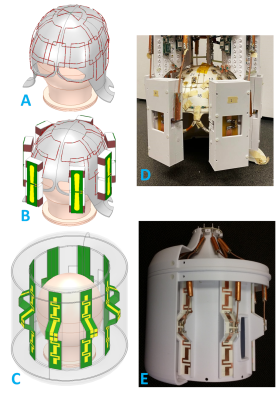
Figure 2. EM simulation
models of (A) 32ch Rx-only loop, (B) 32ch hybrid loop-NODES, and (C) 8ch TxRx
bumped dipole arrays. Experimentally used (D) 32ch hybrid and (E) 8ch TxRx
coils.
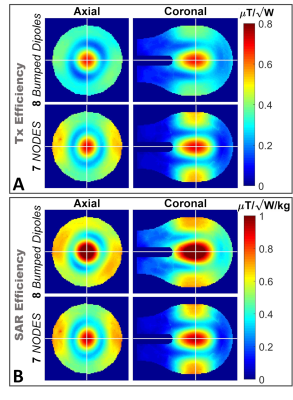
Figure 3. Tx
performance of the 7 TxRx NODES dipole array compared to 8 TxRx bumped dipole
array. (A) Tx and (B) SAR efficiency maps inside a uniform phantom.
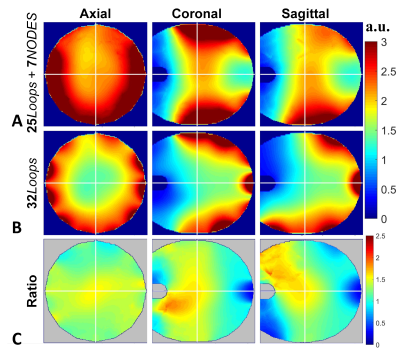
Figure 4. Numerically
obtained ISNR maps using (A) 32ch hybrid loop-NODES array and (B) 32ch Rx-only
loop array. (C) Ratio maps between ISNR of the two coils.
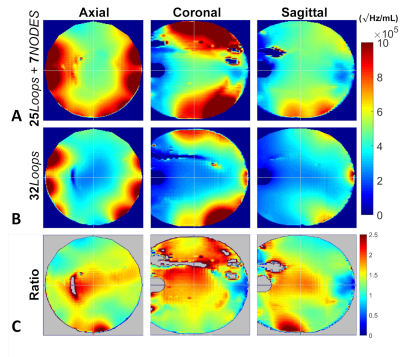
Figure 5.
Experimentally obtained ISNR maps using (A) 32ch hybrid loop-NODES array and
(B) 32ch Rx-only loop array. (C) Ratio maps between ISNR of the two coils.
DOI: https://doi.org/10.58530/2023/3913