Synopsis

Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction

Keywords: artificial intelligence, image reconstruction, perfusion

Cardiac magnetic resonance first-pass contrast-enhanced myocardial perfusion imaging is valuable for evaluating coronary artery disease¹. 2D Cartesian perfusion imaging using compressed sensing (CS)-based reconstructions such as L1-SENSE² enables fast and high-resolution imaging, but whole-heart coverage cannot be achieved without simultaneous multi-slice (SMS) acquisitions and the CS-based iterative reconstruction takes ~30 minutes per slice. To address this, we have developed a deep learning-based motion-corrected rapid image reconstruction for high-resolution Cartesian perfusion imaging at 3 Tesla, for both 2D and SMS MB=2 acquisitions, which provides fast and high-quality motion-corrected reconstruction and makes rapid online reconstruction feasible.

Introduction

First-pass contrast-enhanced myocardial perfusion imaging is valuable for evaluating coronary artery disease¹. Currently, clinical 2D Cartesian perfusion imaging using CS-based image reconstruction such as L1-SENSE provides fast and high-resolution imaging, but it cannot provide whole-heart coverage. CS-based Cartesian SMS perfusion imaging can provide whole-heart coverage but is limited by slow reconstruction (~30 minutes per series).

Motion correction (MOCO) improves qualitative assessment and enables pixel-wise quantification. However, accurate MOCO is time consuming.

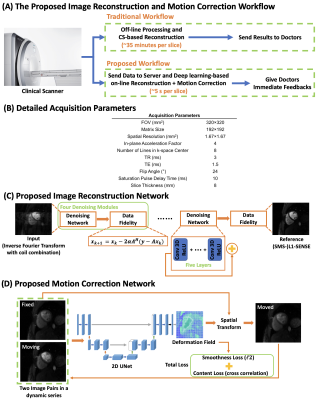
These limitations impede the clinical on-line translation of high-resolution Cartesian perfusion imaging. To address this, we sought to develop a fully automatic deep learning-based (DL) motion-corrected reconstruction technique for Cartesian 2D and SMS high-resolution perfusion imaging to provide rapid and high-quality reconstruction, advancing the clinical workflow (Figure 1-A).

Methods

Data Acquisition and Image Reconstruction: The perfusion sequence (Figure 1-B) utilized a Poisson-disc sampling patterns along phase encoding direction³ with an in-plane acceleration factor of 4 (R=4). For SMS, CAIPIRINHA phase modulation and an SMS factor of 2 was adopted⁴(R=8).

Due to the unavailability of the fully sampled perfusion data, a state-of-art CS-based reconstruction: (SMS)-L1-SENSE, which is an extension of k-t SPARSE-SENSE reconstruction⁵, served as the reference for network training:
$$\underset{x}{\operatorname{argmin}}\|\Phi F S x-y\|_2^2+\lambda\|\Psi x\|_1$$
where $$$x$$$ is the images to be reconstructed, $$$S$$$ is the coil sensitivity maps estimated from the calibration images⁶, $$$F$$$ is the Fourier operator, $$$\Phi$$$ is the phase modulation⁴, $$$y$$$ is the k-space data, $$$\Psi$$$ is the finite time difference sparsifying operator and $$$\lambda$$$ balances between data consistency and sparsity. $$$\lambda=0.05M_0$$$ is chosen where $$$M_0$$$ was the maximal magnitude value of the initial images derived by setting $$$\phi$$$ as 0 and executing the algorithm once.

Image Reconstruction Network: Figure 1-C shows the proposed physics-driven unrolled network consisting of several denoising modules, and each module has a ResNet-based⁸ denoiser and data fidelity update that preserves fine features of image content. Four repetitive modules were implemented, which was the maximum denoising capacity that the network can achieve. Shared weights were utilized for each denoising module⁹.

2D and SMS networks were trained separately with an $$$\ell_1$$$ loss. The inputs to the network were single-channel complex-valued image series after inverse Fourier transform and coil combination⁶. The real and imaginary parts were concatenated, and the complex-valued convolution was enforced¹⁰. The denoising module for SMS network was enforced on each slice separately, and then the data fidelity update was conducted jointly on both slices.

MOCO Network: A 2D U-Net was utilized to estimate the deformation field between two frames in a series (Figure 1-D)¹¹. The inputs are two image pairs reconstructed using (SMS)-L1-SENSE. The deformation field is estimated between image pairs and then applied on the moving image to minimize the difference to target image.

As perfusion images contain dynamically varying contrast, cross correlation, which is insensitive to contrast variation, is utilized as loss function. The smoothness of the deformation field is also incorporated in the loss function to enforce abrupt drifting of the deformation field¹¹.

Experimental Setup: 30 perfusion data from 10 healthy volunteers and 10 patients undergoing clinical CMR studies with gadolinium on 3 T scanners (SIEMENS Prisma/Skyra) were studied.

For reconstruction networks, 30 2D slices from 10 subjects and 30 SMS slices from 10 subjects were used to train the 2D and SMS networks, respectively. Another 15 2D slices from 5 subjects and 30 SMS slices from 5 subjects were used for testing.

The data from the reconstruction network was also used to train the MOCO network.

Training and testing were conducted on a NVIDIA Tesla A100 GPU (80 GB memory), and the (SMS)-L1-SENSE reconstruction was conducted on a server with an Intel i7-7700K CPU (4.20 GHz) and 128 GB memory. The training was conducted for 100 epochs using PyTorch.

Image Analysis: SSIM¹² was used to evaluate the reconstruction performance. Images reconstructed by DL and (SMS)-L1-SENSE were also blindly graded by an experienced cardiologist (5, excellent; 1, poor). The reconstruction time per series (40 frames) was also evaluated. For MOCO, the second-order derivative of the voxel-wise time-intensity values were computed to analyze the temporal smoothness¹³.

Results

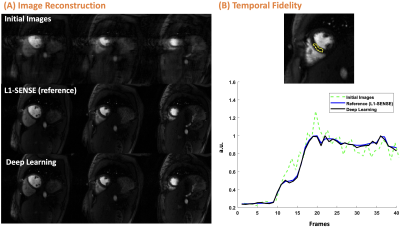
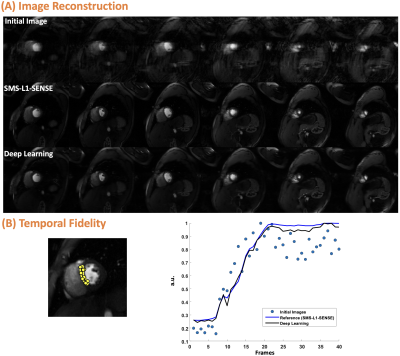
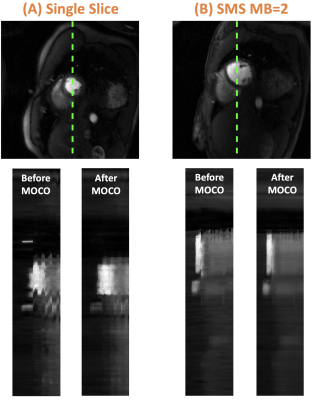
For reconstruction, the SSIM of both 2D and SMS was 0.95 [0.93, 0.96]. For 2D, image quality scores were 4.5 [4.5 ,5] vs. 4.5 [4, 4.6] for L1-SENSE and DL, respectively. For SMS, scores were 4.5 [4.5, 4.5] vs. 4.5 [4.1, 4.5] for SMS-L1-SENSE and DL, respectively. DL results were NOT inferior to CS reconstruction (p>0.05). Figure 2 and 3 show example cases undergoing clinical 2D and SMS perfusion imaging, respectively. Video 1 presents the perfusion video of the case shown in Figure 2.

Figure 4 shows the MOCO for cases with 2D and SMS acquisitions. x-t profile shows excellent performance of the proposed technique. The second-order derivative of 2D and SMS before and after MOCO were 0.25 vs. 0.22 and 0.26 vs.0.23, respectively, demonstrating better temporal smoothness after MOCO.

The reconstruction and MOCO time were ~3 s and ~1 s per series, while the time of using (SMS-)L1-SENSE with 30 iterations was ~30 minutes.

Conclusion

The proposed DL-based motion-corrected image reconstruction technique enabled rapid and high-quality reconstruction for 2D and SMS MB=2 high-resolution Cartesian first-pass perfusion imaging at 3 T.

Acknowledgements

This work was supported by NIH R01 HL131919 and Wallace H. Coulter Foundation Grant.

References

1. Gulati M, Levy PD, Mukherjee D, et al. 2021 AHA/ACC/ASE/CHEST/SAEM/SCCT/SCMR Guideline for the Evaluation and Diagnosis of Chest Pain: A Report of the American College of Cardiology/American Heart Association Joint Committee on Clinical Practice Guidelines. Circulation 2021;144:e368–e454.

2. Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magnetic Resonance in Medicine 2010;64:767–776.

3. Chen X, Salerno M, Yang Y, Epstein FH. Motion-compensated compressed sensing for dynamic contrast-enhanced MRI using regional spatiotemporal sparsity and region tracking: Block low-rank sparsity with motion-guidance (BLOSM): BLOSM: Block Low-rank Sparsity with Motion-guidance. Magnetic Resonance in Medicine 2014;72:1028–1038.

4. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magnetic Resonance in Medicine 2005;53:684–691.

5. Feng L, Srichai MB, Lim RP, et al. Highly accelerated real-time cardiac cine MRI using k–t SPARSE-SENSE. Magnetic Resonance in Medicine 2013;70:64–74.

6. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magnetic Resonance in Medicine 2000;43:682–690.

7. Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magnetic Resonance in Medicine 2013;69:571–582.

8. He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition. 2015.

9. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Transactions on Medical Imaging 2019;38:394–405.

10. Cole E, Cheng J, Pauly J, Vasanawala S. Analysis of deep complex-valued convolutional neural networks for MRI reconstruction and phase-focused applications. Magnetic Resonance in Medicine 2021;86:1093–1109.

11. Balakrishnan G, Zhao A, Sabuncu MR, Guttag J, Dalca AV. VoxelMorph: A Learning Framework for Deformable Medical Image Registration. IEEE Transactions on Medical Imaging 2019;38:1788–1800.

12. Zhou Wang, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing 2004;13:600–612.

13. Scannell CM, Villa ADM, Lee J, Breeuwer M, Chiribiri A. Robust Non-Rigid Motion Compensation of Free-Breathing Myocardial Perfusion MRI Data. IEEE Transactions on Medical Imaging 2019;38:1812–1820.