3891
Overview of Complex-valued Image Reconstruction for CS-MRI Using Real-valued CNN with Symmetrical Signal Under-Sampling
Shohei Ouchi1, Itona Fukatsu1, Kazuki Yamato1, and Satoshi Ito1
1Utsunomiya University, Utsunomiya, Japan
1Utsunomiya University, Utsunomiya, Japan
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Machine Learning/Artificial Intelligence
Complex-valued CNN based image reconstruction methods have been proposed to correspond to MR images with a spatial phase variation. However, using those CNN may lead to over-fitting because CNN layers for complex numbers are requires large number of parameters than real-valued CNN. We previously proposed a reconstruction method for complex-valued image using a real-valued DnCNN by introducing a symmetrical k-space under-sampling. In this study, we introduced this method to U-Net and ADMM-CSNet. Reconstruction experiments showed that a real-valued CNN has the possibility to have the same or better performance as a complex-valued CNN without perform complex calculations.Introduction
MR images have spatial phase variation due to the inhomogeneities of the static field strength or the differences in magnetic susceptibility of living tissue, and therefore, each pixel value in an MR image becomes a complex number. Therefore, it is essential to take spatial phase variation into account in the compressed sensing (CS) image reconstruction. Various approaches have been made to reconstruct complex-valued images in CNN-CS [1][2]. Recently, some approaches use complex-valued CNN[3-5], however, it requires complex computation, batch regularization, and activation functions to correspond to complex numbers, which increases computational complexity and training time. Furthermore, the number of parameters used for learning is large, which may lead to over-fitting as the network goes deeper. We have proposed a reconstruction method for complex-valued images using a real-valued CNN by introducing a symmetrical k-space under-sampling, and preliminary studies using DnCNN[6] were presented. In this study, we added U-Net[7] for image-to-image space learning and ADMM-CS-Net[2] for unrolling model-based learning to compare the overall reconstruction performance.Method
Let $$$s({\bf k})$$$ and $$$\rho(x)$$$ be MR signal and spin density distribution, respectively, then MR signal $$$ s({\bf k})$$$ can be expressed as Eq. (1) ignoring the spin-spin relaxation time and the spin-lattice relaxation time:$$s({\bf k})=\int \rho({\bf x}) e^{-j \phi({\bf x})} e^{-j({\bf k \cdot x)}} d{\bf x}\nonumber ={\cal F}\left[ \rho({\bf x}) e^{-j \phi({\bf x})} \right] ...(1),$$ where $$$\phi(x)$$$ is a spatial phase variation on the image due to imperfection in the MRI equipment and inhomogeneities in the main static magnetic field and F is the operator of the Fourier transform. The real and imaginary part of the complex image $$$\rho(x) \exp^{-j \phi(x)} $$$ can be written as follows: $${\cal F}\left\{ {\rm Re} \left[ \rho({\bf x}) e^{-j \phi({\bf x)}} \right] \right\} =\!\frac{1}{2}{\cal F}\left\{ \rho({\bf x}) e^{-j \phi({\bf x)}}\!\! +\!\! \rho({\bf x}) e^{j \phi({\bf x)}} \right\} =\frac{1}{2} \left\{ s({\bf k})+s({-\bf k})^{*} \right\} ...(2),$$ $${\cal F}\left\{{\rm Im}\! \left[ \rho({\bf x}) e^{-j \phi({\bf x)}} \right] \right\} =-\frac{j}{2} {\cal F}\left\{ \rho({\bf x}) e^{-j \phi({\bf x)}}\!\! - \!\! \rho({\bf x}) e^{j \phi({\bf x)}} \right\} =-\frac{j}{2} \left\{ s({\bf k})-s(-{\bf k})^{*} \right\} ...(3),$$When the coordinates of the sampled signal are not only random but also symmetric with respect to the origin, the calculation of Eqs. (2) and (3) are possible[8], which means that the real and imaginary parts of the complex image can be reconstructed independently using a real-valued CNN. Figure 1 shows an example of a sampling pattern for two-dimensional imaging where the sampling points are selected randomly so as to be symmetric with respect to the origin for the phase encoding direction. According to this method, there is no need to estimate the phase distribution or perform complex calculations; it is simply a matter of reconstructing a real-valued image. In this study, the proposed scheme shown in Fig.1 and Fig.2 was introduced to DnCNN[6] and U-Net[7], which are representative CNNs used in image domain learning, and ADMM-CSNet[2], which is classified as transform learning, for complex image reconstruction.
Result & Discussions
The dataset used for this work consisted of 183 images acquired with Canon Medical Systems 1.5 T MRI scanner; 75 T1-weighted (T1W) sagittal images, 75 T2-weighted (T2W) sagittal images, 6 FSBB (Flow Sensitive Black Blood) axial images, and 27 T2W axial images. The imaged subjects were healthy and informed consent was obtained. In this study, we focused on Cartesian coordinate sampling. Signal under-sampling was applied for the phase encoding direction. We call methods reconstructing real and imaginary part independently as RI-U-Net, RI-ADMM-CSNet and RI-DnCNN to distinguish them from ordinary U-Net, ADMM-CSNet and DnCNN. To compare the reconstruction performances, magnitude and phase estimation method using CNNs(Mag&phase)[1], complex-valued CNN (ComplexCNN)[3][9][10] were also evaluated. The relationship between the amount of signal and the PSNR of the reconstructed image is shown in Fig. 3, and the time for learning CNN or reconstruction is shown in Fig.4. Reconstructed images at 20% and 40% sampling rates are shown in Figures 4. RI-U-Net showed a slightly higher PSNR than ComplexCNN for all signal sampling rates. ComplexCNN involves complex derivatives, but the deeper the layer, the more difficult it is to compute the gradient. These factors resulted in the higher PSNR for the proposed RI-U-Net. RI-ADMM-CS-Net has a lower PSNR when sampling rate is 20%, while it has the highest PSNR when sampling rates are 30% and 40%. Comparing the enlarged images shown in Fig.5, the image by RI-ADMM-CSNet has a larger smoothing effect. This results in a smaller reconstruction error, which is considered to be the reason for the highest PSNR at 30% and 40%. In contrast, RI-U-Net and ComplexCNN restore the detailed structure well. These experiments show that a real-valued CNN has the possibility to have the same or better performance as a complex-valued CNN by introducing symmetrical signal under-sampling. Figure 4 shows that RI-U-Net requires less time for learning and reconstruction than complexCNN. This scheme has the potential to further improve performance by deepening real-function CNNs.Conclution
The method of reconstructing complex-valued images by a real-valued CNN using symmetric signal acquisition has shown the possibility of achieving reconstruction performance comparable to that of a complex type CNN.Acknowledgements
This work was supported in part by JSPS KAKENHI grants 19K04423, 21J14120. We would like to thank Canon Medical Systems.References
- D. Lee et al., Deep Residual Learning for Accelerated MRI Using Magnitude and Phase Networks. IEEE Tran BME 2018; 65: 1985-1995.
- Y. Yang et al., ADMM-CSNet: A Deep Learning Approach for Image Compressive Sensing. IEEE Tran PAMI, doi: 10.1109/TPAMI.2018.2883941.
- C. Trabelsi et al., Deep complex networks. ICLR2018.
- E.Cole et al., Analysis of deep complex-valued convolutional neural networks for MRI reconstruction and phase-focused applications. Magn Reson Med 2021; 86:1093-109.
- S. Wang et al., DeepcomplexMRI: Exploiting deep residual network for fast parallel MR imaging with complex convolution. Mang Reson Imaging 2020; 68:136-47.
- K. Zhang et al., Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Tran Image Proc 2017; 26: 3142-3155
- O. Ronneberger et al., U-Net: Convolutional Networks for Biomedical Image Segmentation. MICCAI2015, 234-241, Munich, Germany.
- S. Ito et al., Compressed sensing for magnetic resonance images with phase variations. ICASSP2014, doi: 10.1109/ICASSP.2014.6854876.
- complexPyTorch. https://github.com/wavefrontshaping/complexPyTorch
- MW. Matthès et al., Learning and Avoiding Disorder in Multimode Fibers. Physical Review X 2021; 11, 021060, 2021. https://doi.org/10.1103/PhysRevX.11.021060.
Figures
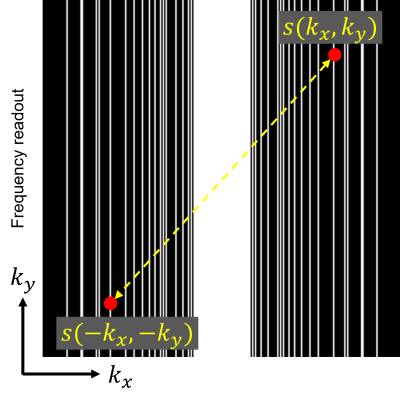
Symmetrical
signal subsampling with respect to the origin of k-space that is used in
proposed method.
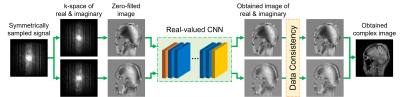
Reconstruction
flow of complex-valued image using real-valued CNN.
Real
and imaginary part of complex image are reconstructed independently as
real-valued image. We used U-Net, DnCNN and real functional ADMM-CSNet. Data
Consistency step is used after estimation by CNN.
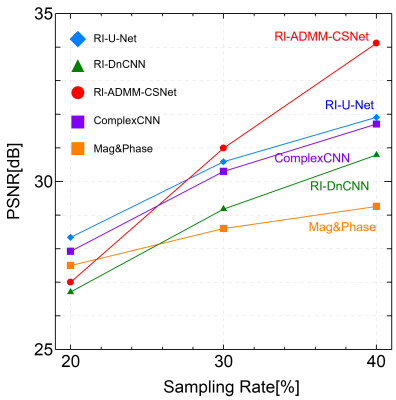
Comparison
of PSNR between proposed method (RI-U-Net, RI-DnCNN, RI-ADMM-CSNet),
Mag&Phase, ComplexCNN.

Comparison of training and
reconstruction time between the methods used in the experiments.
Training of CNN were done using 122 images.
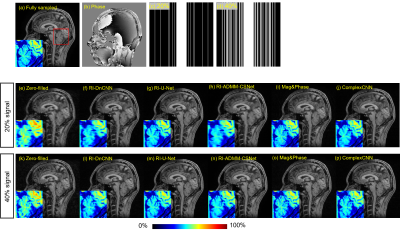
Comparison
of reconstructed images using proposed scheme (RI-U-Net, RI-DnCNN,
RI-ADMM-CSNet) and other methods (Mag&Phase, ComplexCNN).
Sampling
rates are 20% and 40%. Enlarged images in color scale of the area indicated by
the red frame in (a) are shown in the lower left corner of each image.
DOI: https://doi.org/10.58530/2023/3891