Synopsis

Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction, Plug-and-play, denoiser

In this work, we demonstrated that a deep-learning based denoiser trained on a limited dataset of first-pass myocardial perfusion MRI studies enables low-latency image reconstruction using the plug-and-play iterative reconstruction framework. Our proof-of-concept results suggest that the data-adapted denoiser resulted in superior performance versus a generic denoiser especially if there are constraints on the number of iterations (total computation time) which is the case in certain clinical settings specifically interventional MRI. Our findings also imply that radial sampling may be a more desirable data acquisition strategy for PnP-based image reconstruction in first-pass MP MRI studies.

Introduction

In recent years, dynamic first-pass myocardial perfusion (MP) MRI has evolved into the modality of choice for accurate detection of ischemic heart disease. However, high-resolution MP MRI requires a high level of spatiotemporal (2D+time) acceleration which is challenging given the inherently low signal-to-noise ratios during dynamic imaging. As is the case for other spatiotemporal compressed sensing reconstruction problems, most techniques for highly accelerated MP MRI encode the spatiotemporal priors or constraints in the iterative reconstruction process — often in form of regularization terms added to the data-consistency term to form a penalized least-squares functional. As an alternative to the conventional approach for solving such computationally intensive optimization problems, plug-and-play (PnP) methods [1,2] iteratively apply “off the shelf” or generic image denoisers that serve as a “regularization engine” in the image reconstruction process. In this work, we investigate the impact of two major factors in designing the imaging strategy on the performance and convergence rate (latency) of image reconstruction for MP MRI using PnP approaches: (a) the choice of the PnP denoiser engine (generic off-the-shelf denoiser vs. patient data-adapted), and (b) the choice of sampling trajectory (Cartesian vs. radial).

Methods

The inverse problem for image reconstruction in MRI can be expressed as:
$$y=Ax+e$$where $$$y$$$ denotes the acquired k-space signal, $$$x$$$ is the underlying or “true” image, $$$A$$$ is the combination of coil sensitivities, sampling scheme and Fourier encoding, and lastly $$$e$$$ is the noise vector. Eq$$$(1)$$$ can be solved by solving the following optimization problem:$$\hat{x} = argmin_x \{\frac{1}{2\sigma^2} \|y-Ax \|_2^2 + \phi(x)\}$$where $$$\phi(x)$$$ is the regularization which enforces the prior known about $$$x$$$. In PnP approaches, variable splitting is used to decouple the data consistency and regularizations terms, and the following set of iterative equations are solved (for $$$i=1,...,N$$$) to compute $$$x$$$ and $$$v$$$ using the ADMM approach [3]: $$ x_i = h(v_{i=1} - u_{i-1})$$ $$ v_i = P(x_i + u_{i-1})$$ $$ u_i = u_{i-1} + (x_i - v_i)$$ where $$$h(z) = argmin_x \{\frac{1}{2\sigma} \|y-Ax \|^2 + \frac{1}{2\eta}\|x-z \|^2\}$$$ and $$$z = v_{i-1}-u_{i-1}$$$. In the above, $$$h$$$ enforces data consistency (implemented using a conjugate gradient algorithm) and PnP denoiser, $$$P$$$, enforces the prior.

We used the widely used block matching denoiser BM4D [4] as the generic denoiser engine, $$$P_{gen}$$$. For data-adapted denoiser, $$$P_{da}$$$, we trained a deep neural network (DNN) to learn the residual (target) between the noisy and clean MP MRI images using a dataset consisting of 90 stress/rest MP image series (30 patients with suspected ischemia; 3T scans with 3 short-axis MP slices acquired using SR-prepared FLASH with Cartesian sampling). The training set for DNN denoiser was augmented 5-fold with different realizations of additive white Gaussian noise.

To evaluate the image reconstruction performance, fully sampled data from 15 stress/rest MP image series (acquired in 5 patients) was retrospectively subsampled and virtual coil compression was applied [5]. We ran experiments for three different acceleration factors $$$R\in\{4,6,8\}$$$ to simulate accelerated MP acquisition with a pseudo-random subsampling scheme that varied across time frames as is done in time-interleaved (TGRAPPA) Cartesian acquisition and golden-angle radial acquisition for MP MRI pulse sequences [6,7]. We evaluated the quality of the reconstructed MP image series for denoising engines of $$$P_{da}$$$ and $$$P_{gen}$$$ as well as Cartesian vs. radial sampling with $$$R$$$-fold acceleration based on structural similarity index (SSIM) and peak signal-to-noise ratio (PSNR).

Results

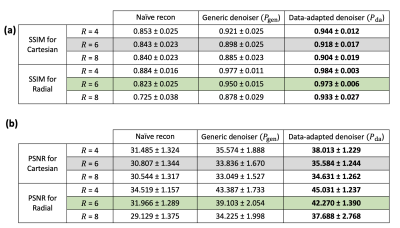
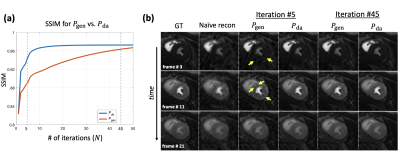
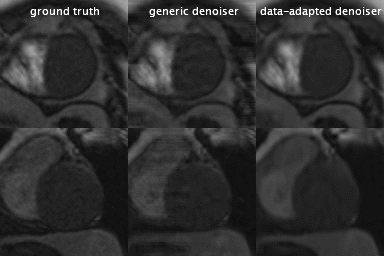
Fig.1 summarizes the image reconstruction performance (in terms of SSIM and PSNR) for $$$R\in\{4,6,8\}$$$ with a fixed number of iterations $$$N=30$$$. As expected, our data-adapted denoiser outperformed the generic denoiser across the board. More interestingly, Fig.1 indicate that, independent of the denoiser choice, radial sampling results in better performance. Overall, the best performance was achieved using data-adapted denoiser and radial sampling regardless of the acceleration factor. Fig.2 evaluates the feasibility of low-latency reconstruction: Fig.2a summarizes the cumulative reconstruction performance (average for 15 MP image series) as a function of the number of PnP iterations for radial sampling with a fixed acceleration factor of $$$R=6$$$. As can be seen, the generic denoiser nearly matches the performance of the data-adapted denoiser after $$$N\geq45$$$ iterations. However, the data-adapted denoiser significantly outperforms when only a low number of iterations are used. The latter scenario is pertinent to clinical settings where low-latency image reconstruction is required, e.g., in interventional MRI. In fact, with just $$$N=5$$$ iterations, $$$P_{da}$$$ achieves the same SSIM as what $$$P_{da}$$$ achieves with 25 iterations (5-fold computational acceleration). Fig.2b shows a case comparing the two denoising engines at three stages of contrast enhancement. Unlike $$$P_{gen}$$$, $$$P_{da}$$$ rapidly converges to a reasonable performance (SSIM = 0.94) in just 5 iterations. Fig.3 dynamically shows reconstruction results for two acquisition slices in the test set with acceleration rate of $$$R=4$$$.

Conclusion

In this proof-of-concept study, we demonstrated that a deep-learning based denoiser trained on a limited dataset enables low-latency image reconstruction for dynamic MP MRI using the plug-and-play iterative reconstruction framework. The superior performance of the data-adapted denoiser versus a generic denoiser is especially noticeable if there are constraints on the number of iterations which is the case in certain clinical settings. Furthermore, our results suggest that radial sampling may be more desirable for PnP-based image reconstruction in first-pass MP MRI studies.

Acknowledgements

No acknowledgement found.