Synopsis

Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction

Deep learning architectures such as Convolutional Neural Networks (CNNs) are widely used alongside fixed k-space undersampling for reconstructing highly undersampled MRI k-space data. However, CNN-based architectures may perform sub-optimally due to their limited ability to capture long range dependencies, and fixed undersampling patterns may not be amenable to optimal reconstruction. We propose dual-domain (image and k-space), transformer-based reconstruction architectures paired with learning-based undersampling to reconstruct undersampled k-space data. Experimental results demonstrate improved reconstruction quality compared to CNN-based (UNet) architecture across 5x to 100x acceleration factors; dual domain outperformed single domain reconstructions.

Introduction

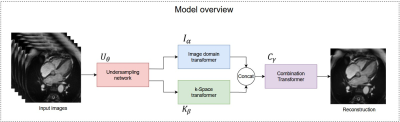
MRI is an inherently slow modality, and despite decades of progress in acceleration (e.g. parallel imaging^1-4 and compressed sensing⁵), acceleration factors remain modest. Recently, there has been great interest in exploring deep learning for reconstructing images from greatly undersampled MRI data. In this work, we present a dual-domain (i.e. image and k-space domain) reconstruction framework using transformers, leveraging their self-attention mechanism to perform image domain anti-aliasing, k-space interpolation, and combining the dual domain reconstruction outputs into a final image domain reconstruction.

Methods

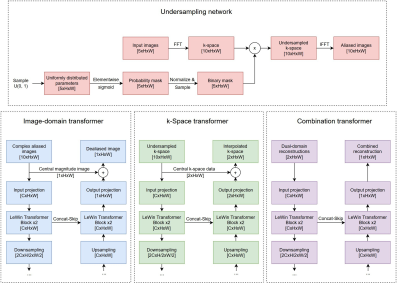
An overview of our model is depicted in Figure 1, and detailed architecture of each sub-network is shown in Figure 2. The model accepts sets of five images at a time. Because cardiac CINE scans consist of a sequence of temporally coherent heart images, using sequences of images as input incorporates temporal information for more robust reconstructions. Let $$${\{x_i\in {\mathbb{R}}^{5\times d}\}}^n_{i=1}\ $$$ denote sets of five full-resolution input images, where $$$i$$$ refers to the $$${i}^{th}$$$ set, $$$d$$$ is the dimension of an image, and $$$n$$$ is total number of image sets. Our model solves the following optimization problem (1) $${\mathrm{min}}_{\theta ,\alpha ,\beta ,\gamma }\ \frac{1}{n}\sum^n_{i=1}{{\left\|C_{\gamma }\left(I_{\alpha }\left(U_{\theta }\left(x_i\right)\right),F^{-1}\left(K_{\beta }\left(F\left(U_{\theta }\left(x_i\right)\right)\right)\right)\right)-x_i\left[3\right]\right\|}^2_2}$$ where $$$U_{\theta }\left(\bullet \right)$$$ transforms images to k-space, performs undersampling parameterized by $$$\theta$$$, and transforms undersampled k-space back to aliased images. $$$I_{\alpha }\left(\bullet \right)$$$ denotes the image domain anti-aliasing function parameterized by $$$\alpha$$$; $$$K_{\beta }\left(\bullet \right)$$$ denotes the k-space interpolation function parameterized by $$$\beta$$$; $$$C_{\gamma }\left(\bullet \right)$$$ denotes the function that combines reconstructions from the two domains, parameterized by $$$\gamma$$$; $$$F\left(\bullet \right)$$$ is the 2D Fourier transform (applied separately to each image); $$$F^{-1}\left(\bullet \right)$$$ is the inverse 2D Fourier transform; $$$x_i\left[3\right]$$$ refers to the third (central) image from the sampled set; and $$${\left\|\bullet \right\|}_2$$$ denotes the L2 norm.
The $$$U_{\theta }$$$ function was implemented by the Undersampling network, which is a modification of the LOUPE network$$${}^{6}$$$ to allow 5 input images at a time. The $$$I_{\alpha }$$$, $$$K_{\beta }$$$, and $$$C_{\gamma }$$$ functions were implemented by the Image-domain transformer, k-Space transformer, and Combination transformer, respectively, all of which are modified versions of the UFormer$$${}^{7}$$$, shown in Figure 2. In the Image-domain transformer, given five temporally correlated and aliased images, the network must learn an encoding that generates one unaliased image that resembles the middle input image. Hence, the network accepts 10-channel input consisting of five complex-valued aliased images, and the output projection was modified to produce a 1-channel residual image. To further facilitate reconstruction of the middle input image, its magnitude image equivalent was added to the residual image to form the output of the Image transformer. Similar modifications were made to produce the k-Space transformer and the Combination transformer, which all encode high dimensional input data and generate reconstructed output.
Experiments were conducted on fully sampled 2D CINE scans acquired in the four-chamber view (UK Biobank). We used ADAM optimizer⁸ to minimize mean squared error (Eq. 1). We also compared transformer-based reconstruction networks with CNN-based reconstruction by replacing the Image, k-Space, and Combination UFormers with UNets. Each variation of the reconstruction network was connected to an undersampling network and trained from scratch to optimize end-to-end undersampling plus reconstruction and to allow a fair comparison. Reconstruction performance was assessed using the Structural Similarity Index Measure (SSIM).

Results and Discussion

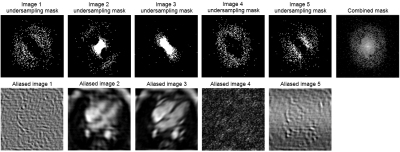
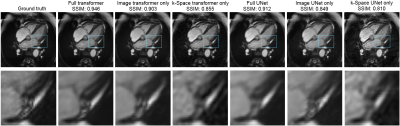
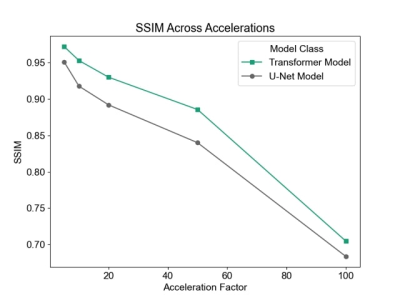
We begin by examining undersampling patterns learned by our model. Figure 3 shows that the shape of the learned sampling pattern varies across the temporal sequence, which is expected because the model should minimize sampling redundancy across a temporally coherent sequence. The second and third sets capture low spatial frequency information, which is responsible for image contrast, while the first, fourth and fifth sets of sampled k-space capture high spatial frequency information, which is responsible for image details such as edges and small features. To visualize the sampling pattern more holistically, the combined mask is shown, which bears resemblance to variable density sampling masks that favor low frequency regions. Figure 4 depicts reconstructions from several variants of the reconstruction network: full (image-domain, k-space, combination) transformers, image-domain transformer only, k-Space transformer only, and comparisons against UNet CNN reconstructions. The full transformer model best preserved valve details, heterogeneity of the myocardium, and the anatomy of all heart structures, and suffered least from blurring artifacts. When reconstructions were performed using a single domain, the Image domain models (Image transformer only, and Image UNet only) outperformed the k-Space-only models, as they better recovered small anatomical details and had less ringing artifacts, seen as striations in the heart chambers. Finally, reconstruction quality, as measured using the SSIM metric, decreased with higher acceleration; however, the transformer-based model outperformed UNet-based model across all acceleration factors (Figure 5).

Conclusion

We proposed a dual domain, transformer-based framework for reconstructing undersampled MRI acquisitions. Our results demonstrated superior performance of the transformer architecture over conventional UNets, and dual-domain versus single-domain reconstructions.

Acknowledgements

This work was supported by the Natural Sciences and Research Council of Canada Discovery Grant [grant #2019-06137], Canadian Institutes of Health Research [grant #PJT 175131], and Canada Foundation for Innovation/Ontario Research Fund [grant #34038].