3881
Uncertainty Estimation for Deep Learning-Based Enhancement of Undersampled Dual-Echo Steady-State Knee MRI1Department of Radiological Sciences, David Geffen School of Medicine, University of California Los Angeles, Los Angeles, CA, United States, 2Department of Bioengineering, University of California Los Angeles, Los Angeles, CA, United States
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Data Analysis, Image Enhancement
Deep learning (DL) based image enhancement of undersampled 3D dual-echo steady-state knee MRI can achieve faster computation times compared to compressed sensing reconstruction. However, it is hard to interpret how DL models work. This introduces the risk of DL-enhanced images containing inaccuracies without the user’s knowledge and thus confounding diagnosis. This work aimed to calculate pixel-wise uncertainty maps for DL-enhanced images by incorporating Monte Carlo Dropout into a 2D UNET to estimate epistemic uncertainty. Analysis showed that the DL-enhanced images achieved good image quality and the spatial uncertainty maps reflected errors, compared to reference images.Introduction
3D dual-echo steady-state (DESS) MRI acquires images of two different contrasts, FID and ECHO, which can be used to rapidly quantify T2 in the knee cartilage1,2 for characterization of osteoarthritis (OA)3,4. To accelerate 3D knee imaging, data undersampling with constrained reconstruction has been investigated5,6. Constrained reconstruction methods have achieved promising results, but are time-consuming and require manual tuning of regularization parameters7,8,9. Deep Learning (DL)-based image enhancement from undersampled data provides rapid inference time and is capable of learning from a large dataset10; however, it is difficult to understand why/how DL-based methods work or even predict the performance of a certain network. In medical image enhancement, image fidelity must be prioritized. Obstruction or elimination of details may confound diagnostic decisions. To overcome this problem, recently there are some works on developing DL networks with uncertainty estimation11,12 to predict error in enhancement tasks. In this work, we investigated the Monte Carlo (MC) Dropout11,13 approach to estimate pixelwise epistemic (or “model”) uncertainty in DL-based enhancement of undersampled 3D DESS knee MRI.Methods
Dataset: 65 3D DESS knee MRI datasets from the SKM TEA dataset10 were used, with 45/10/10 datasets for training, validation, and testing. These datasets were acquired on 3T scanners (GE healthcare) with TE/TR of 5.7/17.9 ms, in-plane resolution of 0.38x0.31 mm2, slice thickness of 1.6mm, elliptical k-space sampling, and factor of 2 parallel imaging. Datasets were first reconstructed using parallel imaging, then retrospectively undersampled in k-space by a factor of 6 using a variable-density pattern (ky-kz corresponded to axial slices) (Figure 1), and coil-combined. Images reconstructed with parallel imaging (without retrospective k-space undersampling) were used as the reference.DL Model: Real and imaginary parts of the two DESS contrasts from each undersampled axial slice (interpolated to 512x512; stacked into 4 channels) were used as the input to the DL model. We used 2D UNET14 with MC Dropout for image enhancement from undersampled data (Figure 2). The network was trained using mean-squared-error loss and the Adam optimizer for 20 epochs. After training, dropout layers were still turned on during inference. Each instance was processed T times (e.g., T=20 in this work), and the pixel-wise uncertainty maps were calculated using $$$Uncertainty=Var[X]=\frac{1}{T}\sum_{t=1}^{T}\left( X_{t}-E[X]] \right)^{2}$$$ . Here, Xt refers to the tth network output for the same instance and E[.] represents expectation operator. The final image enhancement results were generated by taking the average over the T=20 network outputs.
T2 mapping: A dictionary fitting approach was used to calculate T2 maps from the DESS FID and ECHO images2.
Evaluation: We evaluated the results in the testing set. For image quality evaluation, Peak Signal-To-Noise Ratio (PSNR) and Structural Similarity index (SSIM) scores were calculated by comparing DL results to the reference in each axial slice. Absolute difference in the signal magnitudes were calculated between the reference and DL output images and compared with the uncertainty maps. T2 quantification accuracy was evaluated by comparing the cartilage T2 values between DL-based results and the reference using Bland-Altman analysis.
Results
The total training time was 18 hours and the inference time was roughly 8 ms/slice using an NVIDIA A6000 GPU with 48 GB memory. Figure 3 shows representative results obtained using UNET with MC Dropout. The (average±standard deviation) PSNR in the testing set was 36.394±2.44 for FID and 41.164±1.17 for ECHO. The SSIM values in the testing set was 0.853±0.044 for FID and 0.90±0.024 for ECHO. Figure 4 compares the difference image with the uncertainty map for FID and ECHO images. The cartilage T2 values from DL-based and reference results had low mean difference of 0.36 ms (Figure 5).Discussion
Figure 4 shows the visual correspondence between the difference image and the uncertainty map. The brighter regions in the uncertainty map reflect larger differences in the DL-enhanced image compared to the reference. For FID and ECHO images, the regions-of-interest (ROIs) highlight representative areas where larger/smaller differences correspond to larger/smaller uncertainty values respectively. This indicates that these uncertainty maps have the potential to be used as visual guides of the confidence in the DL-enhanced images. The DL-based cartilage T2 mapping results had close agreement with the reference as shown in Figure 5.There are limitations in this work. The current approach calculates uncertainty for the enhanced images, not the T2 maps. Modeling of image uncertainty and the corresponding T2 quantification errors warrants further research. The uncertainty maps of this work are currently considered as visual guides. Additional development of numerical models to associate uncertainty values with image differences could be informative. Future work could also investigate the impact of the errors in the DL-enhanced images on diagnostic tasks, and whether the uncertainty maps could improve confidence in the use of DL-enhanced images.
Conclusion
We applied Monte Carlo Dropout to estimate pixel-wise epistemic uncertainty maps for deep learning-based enhancement of undersampled 3D DESS knee MRI. The uncertainty maps have potential to convey the level of confidence in DL-enhanced images.Acknowledgements
This work was supported in part by Siemens Medical Solutions USA, Inc.
References
[1] Dregely, Isabel, Daniel AJ Margolis, Kyunghyun Sung, Ziwu Zhou, Novena Rangwala, Steven S. Raman, and Holden H. Wu. "Rapid quantitative T2 mapping of the prostate using three‐dimensional dual echo steady state MRI at 3T." Magnetic Resonance in Medicine 76, no. 6 (2016): 1720-1729.
[2] Roux, Marion, Tom Hilbert, Mahmoud Hussami, Fabio Becce, Tobias Kober, and Patrick Omoumi. "MRI T2 mapping of the knee providing synthetic morphologic images: comparison to conventional turbo spin-echo MRI." Radiology 293, no. 3 (2019): 620-630.
[3] Chaudhari, Akshay S., Feliks Kogan, Valentina Pedoia, Sharmila Majumdar, Garry E. Gold, and Brian A. Hargreaves. "Rapid knee MRI acquisition and analysis techniques for imaging osteoarthritis." Journal of Magnetic Resonance Imaging 52, no. 5 (2020): 1321-1339.
[4] Atkinson, Hayden F., Trevor B. Birmingham, Jenna M. Schulz, Codie A. Primeau, Kristyn M. Leitch, Stephany L. Pritchett, D. W. Holdsworth, and J. R. Giffin. "High tibial osteotomy to neutral alignment improves medial knee articular cartilage composition." Knee Surgery, Sports Traumatology, Arthroscopy 30, no. 3 (2022): 1065-1074.
[5] Zibetti, Marcelo VW, Rahman Baboli, Gregory Chang, Ricardo Otazo, and Ravinder R. Regatte. "Rapid compositional mapping of knee cartilage with compressed sensing MRI." Journal of Magnetic Resonance Imaging 48, no. 5 (2018): 1185-1198.
[6] Huang, Chuan, Christian G. Graff, Eric W. Clarkson, Ali Bilgin, and Maria I. Altbach. "T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing." Magnetic resonance in medicine 67, no. 5 (2012): 1355-1366.
[7] Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 58, no. 6 (2007): 1182-1195.
[8] Haldar, Justin P., Diego Hernando, and Zhi-Pei Liang. "Compressed-sensing MRI with random encoding." IEEE transactions on Medical Imaging 30, no. 4 (2010): 893-903.
[9] Kim, Seung-Jean, Kwangmoo Koh, Michael Lustig, and Stephen Boyd. "An efficient method for compressed sensing." In 2007 IEEE International Conference on Image Processing, vol. 3, pp. III-117. IEEE, 2007.
[10] Desai, Arjun D., Andrew M. Schmidt, Elka B. Rubin, Christopher M. Sandino, Marianne S. Black, Valentina Mazzoli, Kathryn J. Stevens et al. "Skm-tea: A dataset for accelerated mri reconstruction with dense image labels for quantitative clinical evaluation." arXiv preprint arXiv:2203.06823 (2022).
[11] Schlemper, Jo, Daniel C. Castro, Wenjia Bai, Chen Qin, Ozan Oktay, Jinming Duan, Anthony N. Price, Jo Hajnal, and Daniel Rueckert. "Bayesian deep learning for accelerated MR image reconstruction." In International Workshop on Machine Learning for Medical Image Reconstruction, pp. 64-71. Springer, Cham, 2018.
[12] Shih, Shu-Fu, Sevgi Gokce Kafali, Tess Armstrong, Xiaodong Zhong, Kara L. Calkins, and Holden H. Wu. "Deep learning-based parameter mapping with uncertainty estimation for fat quantification using accelerated free-breathing radial MRI." In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), pp. 433-437. IEEE, 2021.
[13] Abdar, Moloud, Farhad Pourpanah, Sadiq Hussain, Dana Rezazadegan, Li Liu, Mohammad Ghavamzadeh, Paul Fieguth et al. "A review of uncertainty quantification in deep learning: Techniques, applications and challenges." Information Fusion 76 (2021): 243-297.
[14] Ronneberger, Olaf, Philipp Fischer, and Thomas Brox. "U-net: Convolutional networks for biomedical image segmentation." In International Conference on Medical image computing and computer-assisted intervention, pp. 234-241. Springer, Cham, 2015.
Figures
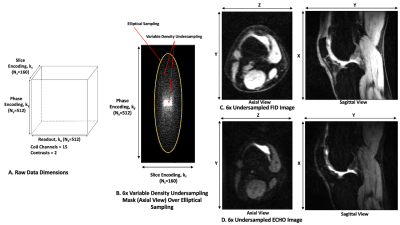
Figure 1: Data characteristics. (A) Data dimensions for the 3D DESS MRI datasets. (B) Axial view of the k-space undersampling mask in (ky, kz). (C-D) Axial and sagittal views of the undersampled images for DESS FID and ECHO contrasts.
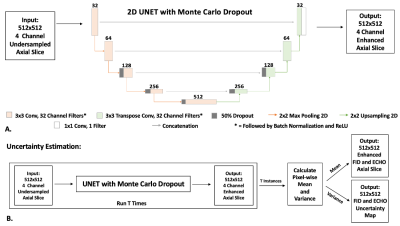
Figure 2: (A) 2D UNET with Monte Carlo Dropout. Dropout layers (p=50%) were added at the beginning of the third, fourth and fifth stages as shown in the figure. The real and imaginary parts of DESS FID and ECHO images from a single axial slice were stacked as 4 channels for the input. (B) For uncertainty estimation, inference was performed T=20 times using the UNET with Monte Carlo Dropout to calculate the enhanced image and a corresponding pixel-wise uncertainty map.
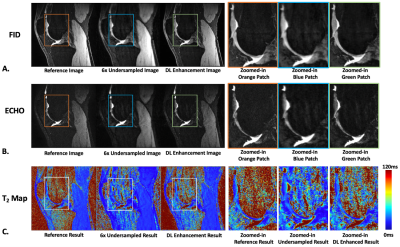
Figure 3: Comparison of reference and deep learning-based image enhancement results in a sagittal slice for (A) DESS FID images, (B) DESS ECHO images and (C) DESS T2 maps.
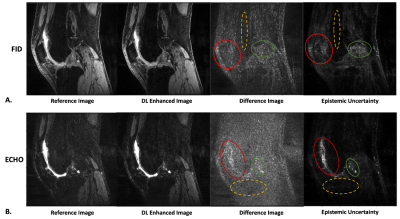
Figure 4: Difference images compared with the uncertainty maps for a single sagittal slice for (A) DESS FID images and (B) DESS ECHO images. The red and green regions-of-interest (ROI) show areas of higher values in the difference images, which correspond to areas of higher values in the uncertainty maps. The dashed yellow ROIs show regions of smaller differences that correspond to lower uncertainty values.
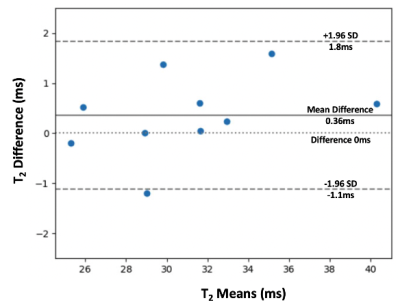
Figure 5: Bland-Altman plot comparing the T2 values within the cartilage of the central sagittal slice calculated using the reference images and DL-enhanced images. The solid line shows the mean difference and the dashed lines show the 95% limits of agreement. We observed a close agreement with low mean difference (0.36ms) and tight limits of agreement.