3879
Accurate Estimation of Background Phase in Virtual Conjugate Coil Expansion Combined with Wave Encoding
Congcong Liu1, Zhuoxu Cui1, Sen Jia1, Zhilang Qiu2, Xin Liu1, Hairong Zheng1, Dong Liang1, and Haifeng Wang1
1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2Case Western Reserve University, Cleveland, OH, United States
1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2Case Western Reserve University, Cleveland, OH, United States
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction
The wave encoding model with virtual conjugate coil (Wave-VCC) extension can provide more powerful MRI-accelerated imaging performance. However, estimating the background phase covering the full frequency range is un-tractable by only acquiring the middle auto-calibration signals (ACS) line during reconstruction. Here, combining a neural network without training, a new method to generate more accurate background phase in Wave-VCC is proposed. Including ablation experiments and comparison, experiments were carried out to verify the feasibility and performance of the proposed methods, respectively.Introduction
Wave encoding is a parallel-imaging (PI) technique that utilizes an additional sinusoidal gradient during the readout to spread aliasing [1]. This is shown to improve the acceleration capabilities of PI as it enables better utility of coil-sensitivity knowledge, achieving a well-posed inverse problem with excellent g-factor performance [2-4]. Additionally, the virtual conjugate coil (VCC) incorporating the complex-conjugate signal of the mirrored k-space region can also improve the quality of PI [5],[6]. Sequentially, the Wave-VCC, which combines VCC and Wave encoding, exploits more prior from wave under the VCC framework to improve acceleration performance [7]. However, the background phase over the full frequency range is untraceable to estimate by acquiring the intermediate low-frequency ACS, which creates the resulting artifacts of phase jumps.Method
The wave-encoded forward model equipped with real channels in the image domain is as follows,$$s=M F_y Ps f\left(k_x, y\right) F_x C_i m \quad i=1, \cdots, N_c \qquad (1)$$where $$$m$$$ is the latent image. The $$$N_c$$$ denotes the total number of the received coil. $$$C_i$$$ presents the weighted coil sensitivity. $$$Psf$$$ is the mathematical representation of wave encoding. The $$$F_x$$$ and $$$F_y$$$ respectively represent the Fourier transform along different dimensions. $$$M$$$ is the sub-sampled pattern. After adding VCC based on the wave encoding model, it becomes as follows,$$s^*=M F_y P s f^*\left(k_x, y\right) F_x e^{-i \varphi} C_i^* m \quad i=1, \cdots, N_c \qquad (2)$$In (2), $$$Ps f^*$$$ and $$$C_i^*$$$ are the conjugate transposes in (1). The background phase is stripped out individually. The latent image $$$m$$$ is represented as a low-rank attribute in the transform domain (in k-space), which can be represented by a deep convolutional neural network [8], similar to [9]. Sequentially, this work focuses on k-space. Both $$$C_i^*$$$ and $$$e^{-i \varphi}$$$ have smoothness properties in the image domain, which have low rankness properties or compact support in k-space. Following [10], we perform the representation of $$$C_i^* C$$$ and $$$e^{-i \varphi}$$$ using the Decoder structure of the parameter generation optimized deep convolutional neural network. Alternatively, (1) and (2) are reformulated as follows,$$b=M F_y P s f\left(k_x, y\right) F_y^{-1} C N N_c^{\varphi} C N N_k^\theta \qquad (3)$$$$b^H=M F_y P s f\left(k_x, y\right) F_y^{-1} C N N_{\varphi}^{\Theta} C N N_{c^*}^\psi C N N_k^\theta \qquad (4)$$Where, $$$m$$$, $$$C_i$$$, $$$C_j^*$$$, and $$$e^{-i \varphi}$$$ are represented by four networks respectively, as shown in Fig. 1. The final designed loss function is as follows,$$\min _{\theta, \varphi, \psi, \Theta} \mathcal{L}(\theta, \varphi, \psi, \Theta)=\left\|f\left(G_{\theta, \varphi, \psi, \Theta}(\mathcal{C})\right)\right\|_F^2 \qquad (5)$$For simplicity, $$$f$$$ in (5) represents the encoding matrix in (3) and (4). This work uses the project gradient descent (PGD) algorithm to iteratively optimize the parameters of the network. Once the parameters of the network are optimized, the complete k-space signal can be reconstructed by inputting only two small low-dimensional random variables.The IRB (institutional review board) approved in vivo human brain experiments were performed on a 3T uMR790 scanner (United Imaging, Shanghai, China). Fully sample the wave-encoded in vivo data, then perform retrospective sub-sampling acceleration experiments. Ablation experiments with different ACS acquisition modalities were performed to verify the feasibility of CSM and background phase generation. Variable density retrospective sub-sampling pattern provides 4x time reduction. The comparison method adopts the classic SENSE and LORAKS [11-14]. The second is to estimate the background phase using a partial Fourier (PF) acquisition pattern. Comparative experiments (6x acceleration, PF sampling pattern) are also carried out to verify the performance of the proposed method.
Results
Accurate estimation of CSM is critical in reconstruction, but CSM is often affected by the number of ACS. In Fig. 2, there are severe artifacts when the ACS is reduced to 14, but the proposed method has superior robustness to fewer ACS, which further verifies that the proposed method is feasible for CSM estimation and has better SNR and contrast preservation. Regardless of whether the number of ACS is 24 or 14 when internal acquisition, the proposed method still has the best reconstruction quality at 4x acceleration. Under the PF sampling template, the proposed method for accelerated reconstruction of WaveVCC gives competitive results with respect to the LORAKS method, and then accurate phase estimates can be verified using the proposed method. It can also be seen from Fig. 5 that the proposed method can also provide superior artifact-free reconstruction quality and requires only a few ACS signals at a 6x acceleration.Conclusion
The proposed method can completely and accurately estimate the background phase in VCC under the Wave framework and provide higher acceleration performance.Acknowledgements
Congcong Liu and Zhuo-Xu Cui contributed equally to this work. The authors thank Prof. Berkin Bilgic and Mohammad Zalbagi Darestani for sharing the WaveCAIPI, and ConvDecoder reconstruction codes. This work was partially supported by the National Natural Science Foundation of China (61871373, 62271474, 81830056, U1805261, 81729003, 81901736, 12026603, and 81971611), the Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000 and XDC07040000), the High-level Talent Program in Pearl River Talent Plan of Guangdong Province (2019QN01Y986), the Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province (2020B1212060051), the Science and Technology Plan Program of Guangzhou (202007030002), the Key Field R&D Program of Guangdong Province (2018B030335001), the Shenzhen Science and Technology Program, Grant Award (JCYJ20210324115810030), and the Shenzhen Science and Technology Program (Grant No. KQTD20180413181834876, and KCXF20211020163408012).References
- Bilgic, Berkin, et al. "Wave‐CAIPI for highly accelerated 3D imaging." Magnetic resonance in medicine 73.6 (2015): 2152-2162.
- Iyer, Siddharth, et al. "Wave-encoding and Shuffling Enables Rapid Time Resolved Structural Imaging." arXiv preprint arXiv:2103.15881 (2021).
- Polak, Daniel, et al. "Highly‐accelerated volumetric brain examination using optimized wave‐CAIPI encoding." Journal of Magnetic Resonance Imaging 50.3 (2019): 961-974.
- Su, Shi, et al. "Accelerated 3D bSSFP using a modified wave-CAIPI technique with truncated wave gradients." IEEE Transactions on Medical Imaging 40.1 (2020): 48-58.
- Blaimer, Martin, et al. "Virtual coil concept for improved parallel MRI employing conjugate symmetric signals." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 61.1 (2009): 93-102.
- Wang, Haifeng, et al. "Improving GRAPPA reconstruction using joint nonlinear kernel mapped and phase conjugated virtual coils." Physics in Medicine & Biology 64.14 (2019): 14NT01.
- Qiu, Zhilang, et al. "Highly accelerated parallel MRI using wave encoding and virtual conjugate coils." Magnetic resonance in medicine 86.3 (2021): 1345-1359.
- Ye, Jong Chul, Yoseob Han, and Eunju Cha. "Deep convolutional framelets: A general deep learning framework for inverse problems." SIAM Journal on Imaging Sciences 11.2 (2018): 991-1048.
- Darestani, Mohammad Zalbagi, and Reinhard Heckel. "Accelerated MRI with un-trained neural networks." IEEE Transactions on Computational Imaging 7 (2021): 724-733.
- Han, Yoseo, Leonard Sunwoo, and Jong Chul Ye. "k-space deep learning for accelerated MRI." IEEE transactions on medical imaging 39.2 (2019): 377-386.
- Pruessmann, Klaas P., et al. "SENSE: sensitivity encoding for fast MRI." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 42.5 (1999): 952-962.
- Wang, Haifeng, et al. "Parameter optimization framework on wave gradients of Wave‐CAIPI imaging." Magnetic resonance in medicine 83.5 (2020): 1659-1672.
- Haldar, Justin P. "Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI." IEEE transactions on medical imaging 33.3 (2013): 668-681.
- Kim, Tae Hyung, et al. "Wave‐LORAKS: Combining wave encoding with structured low‐rank matrix modeling for more highly accelerated 3D imaging." Magnetic resonance in medicine 81.3 (2019): 1620-1633.
Figures
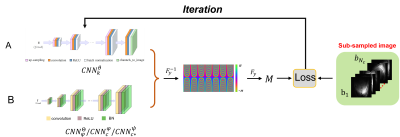
Fig.1 The schematic of the proposed method in this paper that exerts the
function of generation. A is the latent image generative neural network represented
by $$$CNN_{k}^{\Theta}$$$. B denotes the generative network schematic for three variables $$$C_i$$$, $$$C_i^{*}$$$, and $$$e^{-i \varphi}$$$, where the structure of the three
networks is consistent.
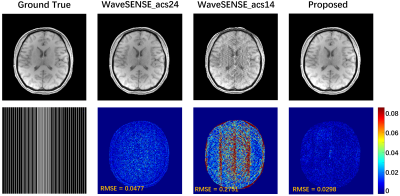
Fig. 2 Simply for latent
images, CSM generation is generated to eliminate the influence of phase
generation. The symbols acs24 and acs14 indicate that the calibration lines are
24 and 14, respectively. The proposed method uses only the additional 14 ACS sampled.
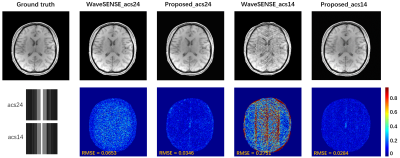
Fig. 3 ACS integrated
acquisition reconstruction results. Intermediate ACS signals were acquired
during retrospective sub-sampling, including 24 and 14 to eliminate the
influence of the ACS acquisition mode on the proposed method.
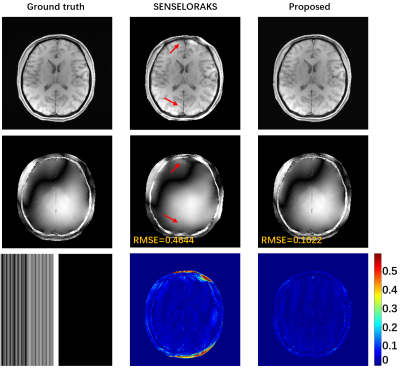
TFig. 4 he intermediate
results of the two methods after wave encoding and channel expansion through
VCC. The sampling acquisition settings are: 1D variable density, ACS=14, PF
sampling pattern. Red arrows mark reconstruction artifacts.
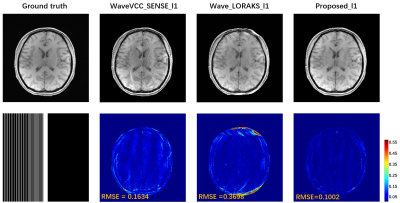
Fig. 5 The accelerated performance of the proposed method is verified in the 6x
PF accelerated pattern with 12 ACS. The
l1 constraint (TV) was imposed to provide better image performance. The comparison method chooses the classic SENSE
and LORAKS which are more used with PF sampling pattern.
DOI: https://doi.org/10.58530/2023/3879