Synopsis

Keywords: Machine Learning/Artificial Intelligence, Diffusion/other diffusion imaging techniques, Uncertainty estimation

We transformed the state-of-the art IVIM-NET for IVIM parameter fitting into a Bayesian Neural Network (BNN). BNNs can estimate uncertainty for quantitative MRI parameters, which is relevant for clinical decision making. We found that training on data with the highest SNR outperformed IVIM-BNNET models trained on matching SNR regarding parameter errors and uncertainties. A region with artificially increased noise could be identified from IVIM-BNNET's uncertainty output. Compared with traditional fitting, IVIM-BNNET achieved comparable accuracy, while being 21 times faster and providing less correlated parameter estimates. Monte-Carlo dropout rate 0.4 provided the best trade-off between low errors and low uncertainty.

Introduction

The intravoxel incoherent motion (IVIM) model¹ aims to simultaneously quantify diffusion and perfusion with diffusion-weighted imaging (DWI). Its parameters are the diffusion coefficient D, the pseudo-diffusion coefficient D^*, the signal fraction of perfusing blood f, and the unweighted signal intensity S₀ for a b-value of 0 s/mm². A deep neural network (DNN) called IVIM-NET² was proposed to address challenges in fitting the IVIM model. It achieved state-of-the-art performance in both quality of parameter estimates and speed³. However, IVIM-NET does not provide information on the uncertainty of the parameter estimates, which would be essential for using IVIM in diagnostic and interventional settings. To address this, we propose to transform the IVIM-NET into a Bayesian neural network⁴ (BNN). In DNN models, weights are fixed values, and outputs are point estimates. Different from DNNs, BNNs represent weights as probability distributions and use Bayes' Theorem to perform inference given measured input data. Among various BNN variants, the Monte-Carlo dropout-based method⁵ can be used directly to approximate output probability distributions without modifications of the model architecture, making it convenient and efficient. Tracking probability distributions instead of weights introduces stochastic components, allowing BNNs to obtain uncertainty estimates from multiple inference passes. We evaluate this design flow by converting IVIM-NET into a BNN and validate IVIM-BNNET against traditional fitting.

Methods

A previously published^3,6 IVIM dataset containing one patient with pancreatic ductal adenocarcinoma was used. It contained diffusion-weighted EPI images with matrix size 144×144 pixels and 21 slices sampled at 104 diffusion-weightings (b-values 0, 10, 20, 30, 40, 50, 75, 100, 150, 250, 400 and 600 s/mm²). Simulated data for training were generated using the IVIM model equation for the same set of b-values:
$$S(b)=S_0\left[(1-f)e^{-bD}+fe^{-bD^{*}}\right]$$
S₀ was set to 1 for training data generation, since the IVIM-NET uses normalised inputs S(b)/S₀. The other parameters were drawn randomly from f ∈ [0.01, 0.5], D ∈ [0.3, 2.5]×10^{-3} mm²/s and D^* ∈ [0.02, 0.2] mm²/s. In addition, zero-mean Gaussian noise with standard deviation S₀/SNR was added to the calculated signal intensities. Signal-to-noise ratios (SNR) of 5, 15, 20, 30 and 50 were used.
In IVIM-NET, dropout layers⁷ are used to regularize the output of every fully connected layer during the training phase. To convert the IVIM-NET into IVIM-BNNET, we replaced these dropout layers with Monte-Carlo dropout layers⁵. The dropout rate corresponds to the probability of discarding the output of a neuron during training and inference. Separate IVIM-BNNET models were trained on simulated data for each SNR level, where one additional model was trained on combined data from all simulated SNR values. The same loss function as for IVIM-NET was used: From the predicted IVIM parameters of a forward pass, the signal S_net(b) was calculated using the IVIM equation and the mean square error (MSE) between S_net(b) and the input S(b)/S₀ was used as loss function. From IVIM parameters obtained from 128 forward passes of the IVIM-BNNET parameter for the same input parameters, the average parameter estimates, standard deviations and correlation matrices are calculated.
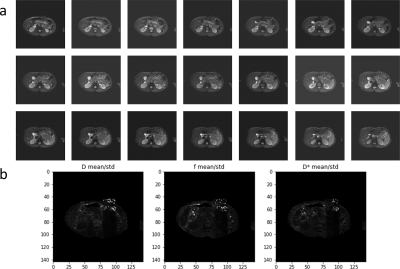
For validation noise was artificially increased in a square region of the patient images by adding zero-mean Gaussian noise with an SNR of 5 scaled by the 99^th percentile of pixel values in each image. Pixels for which the ratio mean/std from the 128 samples was above the 99.8 percentile threshold were highlighted.
Using 1000 synthetic data samples generated as described above for each SNR value, the IVIM-BNNET performance was evaluated against a non-linear least squares fit of the IVIM model using Python's curve_fit. Mean relative error, mean relative standard deviation, correlation matrices and running time were compared.

Results

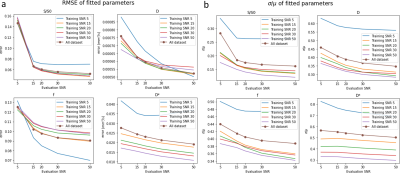
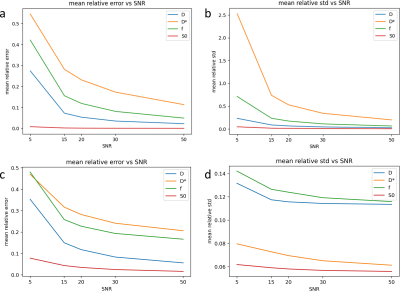
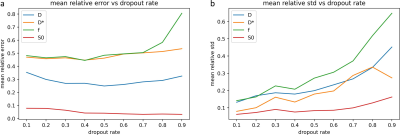
Fig. 1 shows error and uncertainty of IVIM-BNNET models with different training SNRs. Error and uncertainty decrease with evaluation SNR, where the model with highest training SNR outperforms models trained with matching SNRs. Fig. 2 shows example in vivo data with a region of artificially amplified noise, where the uncertainty results from IVIM-BNNET highlight the uncertain regions of the parameter map. Fig. 3 shows relative error and uncertainty versus SNR for traditional and IVIM-BNNET methods, where IVIM-BNNET achieves comparable accuracy with lower uncertainty. Fig. 4 shows the relative error and uncertainty versus dropout rate of IVIM-BNNET, where a dropout rate of 0.4 provides the best compromise between maintaining low error and uncertainty. Fig. 5 shows the correlation between the 4 IVIM parameters for traditional fitting and IVIM-BNNET, which shows less correlation between parameters than traditional fitting. Correlation values are close to 0 except between f and S₀. Correlation decreases with dropout rate. For fitting a test set of 1,000,000 samples, IVIM-BNNET was 21 times faster than Python's curve_fit (5 vs 107 min).

Discussion and Conclusion

We developed a design flow to transform the state-of-the art IVIM-NET into a BNNET, which enables uncertainty estimation of IVIM parameters. Initial results demonstrate the expected behaviour that error and uncertainty decrease with SNR. A region with artificially increased noise could be identified from the IVIM-BNNET's uncertainty output, which could be valuable for clinical decision making. Compared with traditional fitting methods, IVIM-BNNET achieves comparable accuracy with faster running speed, while providing less correlated parameter estimates. Being computationally expensive, we plan to implement IVIM-BNNET on FPGA-based accelerators.

Acknowledgements

This research project was supported by the CRUK Convergence Science Centre at The Institute of Cancer Research, London, and Imperial College London (A26234).